
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Комплексные числа
|
|
|
|
На множестве С вводятся понятия функции, предела таким образом, что соответствующие понятия действительного анализа рассматриваются как частный случай. Естественно, при этом сохраняются известные свойства функций действительного переменного: теоремы о пределах, правила дифференцирования, формулы интегрирования и т.д. Однако, благодаря расширению класса функций, частым случаем которых являются функции действительного переменного, появляются новые свойства. Например, доказывается, что из существования производной функции следует существование ее производных n-го порядка в области. Устанавливается, что все элементарные функции связаны между собой: тригонометрические функции выражаются через показательную функцию, а обратные тригонометрические - через логарифмическую. Значительно глубже, чем в анализе функций действительного переменного, развита геометрическая теория - конформные отображения. Благодаря сочетанию аналитических и геометрических методов теория функций комплексного переменного находит широкое применение в других разделах математики и прикладных задачах.
1. Определить мгновенное значение напряжения на входе электрической цепи, если
U 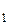 =50e
=50e 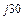 ,B; U
,B; U 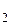 =50e
=50e 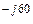 ,B
,B
U 
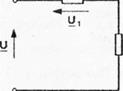
 2. Записать комплексное сопротивление цепи в алгебраической форме, если ток и напряжение указаны на рис.
2. Записать комплексное сопротивление цепи в алгебраической форме, если ток и напряжение указаны на рис.
3. Изобразить на комплексной плоскости и записать в показательной форме токи и напряжения:
а) U = -40+j40,B; I = 3-j4,A
б) U = 40- j40,B I = -3-j4,A
в) U = - 40- j40,B I = -3+j4,A
4. Определить комплексное сопротивление цепи, если
i(t)=14,1sin(10t + 60), A
u(t)=14,1sin(10t - 30), B
5. Определить комплексные сопротивления

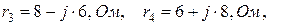
6. Определить коэффициент А четырехполосника по формуле 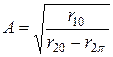 , если известно, что
, если известно, что
r 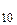 = 6+ j8, OM r
= 6+ j8, OM r  = 6+ j8, OM
= 6+ j8, OM
r 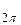 = 6- j8, 0M
= 6- j8, 0M
7. Определить волновое сопротивление линии по формуле 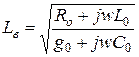
если R 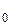 , = 0,1
, = 0,1  , g
, g 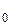 =
= 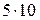
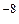 Cиm, 10Lo = 0,4
Cиm, 10Lo = 0,4  , 10С
, 10С 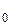 =2.85
=2.85 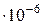

Задача I. В цепи с последовательным соединением элементов г, L, С известно значение полного комплексного сопротивления 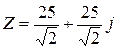
Вычислить полное сопротивление цепи и разность фаз между напряжением и током.
Решение задачи демонстрирует курсантам приложение понятий модуля и аргумента комплексного числа, поскольку полное сопротивление цепи определяется как модуль комплексного числа, а разность фаз — как аргумент этого числа.
Задача 3. Комплексная амплитуда тока, протекающего в цепи,
I = 25е  .
.
Записать мгновенное значение этого тока.
Здесь демонстрируется метод перехода от показательной формы комплексного числа к тригонометрической, что является необходимым элементом решения задач электротехники. Для перехода от комплексной амплитуды к мгновенному значению надо умножить ее на е 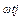 и взять коэффициент при мнимой части от полученного произведения:
и взять коэффициент при мнимой части от полученного произведения:
Задача 4. Колебания тока в электрической цепи, содержащей R, L, С элементы, описываются уравнением
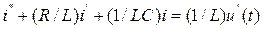
Найти закон протекания тока в цепи, если С=2 мкФ; R=40 Ом; L=4 Гн; u(t)=100 е 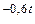 В.
В.
Эта задача позволяет продемонстрировать приложения темы «Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами». В ходе ее решения внимание курсантов следует обратить на то, что, если напряжение в цепи отсутствует или постоянно, уравнение становится однородным, а его общее решение представляет собой закон затухания тока в цепи. Этот ток принято называть переходным. Если же напряжение в цепи изменяется, частное решение получившегося неоднородного уравнения описыва
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 573; Нарушение авторских прав?; Мы поможем в написании вашей работы!