Декартіво добуток графів

Перетин графів

Граф G (X, F) називається перетином графів G1 (X1, F1) і G2 (X2, F2) та позначається G = G1 ∩ G2, якщо X = X1 ∩ X2; F = F1 ∩ F2.

Граф G (X, F) називається декартовим, або прямим добутком графів G1 (X1, F1) і

G2 (X2, F2), якщо X = X1 ´ X2; F = F1 ´ F2.

Для побудови нового графа, що є об'єднанням, перетином або декартовим добутком вихідних графів, необхідно вивчити означення основних операцій і застосувати їх до конкретних графів.

Приклад 10. 1. Знайти граф G (X, F), що є об'єднанням графів G1 (X1, F1) і G2 (X2, F2

G1 (X1, F1) G2 (X2, F2)

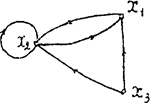
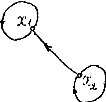
Рисунок 9. Вихідні графи.

X1 = { x₁, x₂, x₃ }; X2 = { x₁, x₂ };

F (x₁) = { x₂ }; F2 (x₁) = { x₁ };

F (x₂) = F (x₃) = { x₁, x₂ }; F2 (x₂) = { x₁, x₂ }.

Знаходимо, що X = X1 U X2 = { x₁, x₂, x₃ }; F = F1 U F2; F (x₁) = F (x₂) = F (x₃)={ x₁, x₂ }.

Геометричне зображення графа G (X, F):

Рисунок 10. Об'єднання графів G1 і G2

2. Знайти граф G (X, F), що є перетином графів G1 (X1, F1) і G2 (X2, F2), розглянутих вище.

Одержуємо X = X1 ∩ X2 = { x₁, x₂ }; F = F1 ∩ F2; F (x₁) = Æ; F (x₂) = { x₁, x₂ }.

Геометричне зображення графа G:

Рисунок 11. Перетин графів G1 (X1, F1) і G2 (X2, F2)

Лекція 13. ЗАДАЧА ПРО МАКСИМАЛЬНИЙ ПОТІК

Однією із найбільш важливих задач теорії графів є задача визначення максимального потоку, що протікає від деякої вершини графа S (джерела) до деякої кінцевої вершини t (стоку). При цьому кожній дузі (x_i, x_j) графа G приписана деяка пропускна спроможність q_ij, вона визначає найбільше значення потоку, що може протікати по даній дузі.

Розглянемо граф G (Х, F) із пропускними спроможностями дуг q_ij, джерелом S і стоком t; S, t Î X. Множини чисел x _ij, визначених на дугах (х_i, х_j) Î F називаються потоками в дугах, якщо виконуються такі умови:

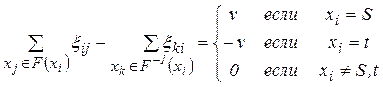(1)

і x _ij £ qij для всіх (xi, xj) Î F.

Рівняння (1) є рівнянням зберігання потоку. Воно підтверджує, що потік, що втікає у вершину, дорівнює, потокові, що випливає з вершини, за винятком джерела S і стоку t. Співвідношення (2) вказує на те, що пропускні спроможності обмежені для кожної дуги графа G.

Задача полягає в знаходженні множин потоків по дугах, щоб величина

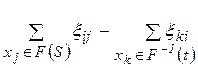(2)

була максимальною.

Ця задача та її варіанти можуть виникати в багатьох практичних застосуваннях.

Наведем визначення величини розріза графа. Разобьемо множину X усех верщин графа на дві взаємно дополнюючих підмножини: 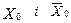, (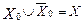) при цьому множина 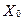містить вершину S (джерело), а множина 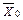- кінцеву вершину t (сток). Множина дуг (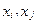), де 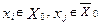називают розрізом графа.

Теорема о максимальном потіке (Форда-Фалкерсона). Максимальне значення сумарного потіка по дугах дорівнюється минимальной пропускной спроможности розріза.

Алгоритм Форда-Фалкерсона

Алгоритм Форда-Фалкерсона складається з двох етапів:

1. Розставляння позначок.

2. Збільшення потоку.

Дата добавления: 2015-06-04