Алгоритм 10

Пример

Ограничения критерия

1. Нижний порог: не менее 2-х испытуемых (n ≥2), каждый из которых прошел не менее 3-х замеров (с≥3).

2. При с=3, n ≤ 9, уровень значимости полученного эмпирического зна­чения χ² _rопределяется по Таблице VII-A Приложения 1; при с=4, n ≤4, уровень значимости полученного эмпирического значения χ² _r определяется по Таблице VII-Б Приложения 1; при больших коли­чествах испытуемых или условий полученные эмпирические значения χ² _rсопоставляются с критическими значениями χ² _r, определяемыми по Таблице IX Приложения 1. Это объясняется тем, что χ² _rимеет распределение, сходное с распределением χ² _r. Число степеней свобо­ды v определяется по формуле:

v =c—1,

где с - количество условий измерения (замеров).

На Рис. 3.5. представлены графики изменения времени решения анаграмм в эксперименте по исследованию интеллектуальной настойчи­вости (Сидоренко Е. В., 1984). Анаграммы нужно было подобрать таким образом, чтобы постепенно подготовить испытуемого к самой трудной - а фактически неразрешимой - задаче. Иными словами, испы­туемый должен был постепенно привыкнуть к тому, что задачи стано­вятся все более и более трудными, и что над каждой последующей анаграммой ему приходится проводить больше времени. Достоверны ли различия во времени решения испытуемыми анаграмм?

Таблица 3.5

Показатели времени решения анаграмм (сек.)

Код имени испытуемого	Анаграмма 1: КРУА (РУКА)	Анаграмма 2: АЛСТЬ (СТАЛЬ)	Анаграмма 3: ИНААМШ (МАШИНА)
1. Л-в 2. П-о 3. К-в 4. Ю-ч 5. Р-о		235*[11]
Суммы
| Средние	10,2	248,8	9,4

Проранжируем значения, полученные по трем анаграммам каж­дым испытуемым. Например, испытуемый К-в меньше всего времени провел над анаграммой 1 - следовательно, она получает ранг 1. На вто­ром месте у него стоит анаграмма 3 - она получает ранг 2. Наконец, анаграмма 2 получает ранг 3, потому что она решалась им дольше двух других.

Сумма рангов по каждому испытуемому должна составлять 6.

Расчетная общая сумма рангов в критерии определяется по формуле:

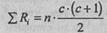
где n - количество испытуемых

с - количество условий измерения (замеров).

В данном случае,

Таблица 3.6

Показатели времени решения анаграмм 1, 2, 3 и их ранги (n= 5)

Код имени испытуемого	Анаграмма 1	Анаграмма 2	Анаграмма 3
	Время (сек)	Ранг	Время (сек)	Ранг	Время (сек)	Ранг
1. Л-в
2. П-о
3. К-в
4. Ю-ч
5. Р-о
Суммы

Общая сумма рангов составляет: 6+15+9—30, что совпадает с расчетной величиной.

Мы помним, что испытуемый Л-в провел 3 минуты и 55 сек над решением второй анаграммы, но так и не решил ее. Поскольку он ре­шал ее дольше остальных двух анаграмм, мы имеем право присвоить ей ранг 3. Ведь назначение трех первых анаграмм - подготовить испытуе­мого к тому, что над следующей анаграммой ему, возможно, придется думать еще дольше, в то время как сам факт нахождения правильного ответа не так существен.

Сформулируем гипотезы.

Н₀: Различия во времени, которое испытуемые проводят над решением трех различных анаграмм, являются случайными.

H₁: Различия во времени, которое испытуемые проводят над решением трех различных анаграмм, не являются случайными.

Теперь нам нужно определить эмпирическое значение χ² _rпо формуле:

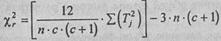
где с - количество условии;

п - количество испытуемых;

Т_i - суммы рангов по каждому из условий.

Определим χ² _rдля данного случая:

Поскольку в данном примере рассматриваются три задачи, то есть 3 условия, с=3. Количество испытуемых n= 5. Это позволяет нам воспользоваться специальной таблицей χ² _r, а именно Табл. VII-A При­ложения 1. Эмпирическое значение χ² _r=8,4 при с=3, n= 5 точно соот­ветствует уровню значимости р=0,0085.

Ответ: Но отклоняется. Принимается H₁. Различия во времени, которое испытуемые проводят над решением трех различных анаграмм, неслучайны (р=0,0085).

Теперь мы можем сформулировать общий алгоритм действий по применению критерия χ² _r.

Подсчет критерия χ² _rФридмана

1.Проранжировать индивидуальные значения первого испытуемого, полученные им в 1-м, 2-м, 3-м и т. д. замерах.

2.Проделать то же самое по отношению ко всем другим испытуемым.

3.Просуммировать ранги по условиям, в которых осуществлялись за­меры. Проверить совпадение общей суммы рангов с расчетной сум­мой.

4.Определить эмпирическое значение χ² _rпо формуле:

где с - количество условии;

п - количество испытуемых;

T_i - суммы рангов по каждому из условий.

5.Определить уровни статистической значимости для χ² _r

а)при с=3, n< 9 - по Табл. VII-A Приложения 1;

б)при с=4, n<4 - по Табл. VII-Б Приложения 1.

6.При большем количестве условий и/или испытуемых - определить количество степеней свободы v по формуле:

v =c-1,

где с - количество условий (замеров).

По Табл. IX Приложения 1 определить критические значения кри­терия χ² при данном числе степеней свободы V.

Если χ² _{r эмп} равен критическому значению χ² или превышает его, различия достоверны.

Дата добавления: 2015-06-04