Цилиндрические проекции

Рис. 4.5

Опишем вокруг глобуса цилиндр, касательный по экватору (рис.4.5). Продолжим плоскости меридианов и параллелей до пересечения с поверхностью цилиндра. Линии пересечения этих плоскостей примем за изображения меридианов и параллелей. Разрежем цилиндр по образующей и развернем на плоскость. В результате получим картографическую сетку в цилиндрической проекции.

Меридианы и параллели изобразятся в этой проекции взаимно перпендикулярными прямыми.

Общее уравнение цилиндрических проекций:

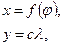(4.11)

где - коэффициент пропорциональности.

Из (4.11) следует, что меридианы всегда – равноотстоящие прямые.

Таким образом, различные цилиндрические проекции различаются видом функции , т.е. способом построения параллелей.

Сравнив азимутальные, конические и цилиндрические проекции напрашивается вывод.

Азимутальная проекция – частный случай конической проекции, когда угол при вершине конуса равен 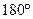, т.е. когда коэффициент пропорциональности 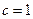(4.8).

С другой стороны, цилиндрическая проекция – также частный случай конической проекции, когда вершина конуса, касательного к глобусу по экватору, удалена в бесконечность, а угол при вершине конуса равен нулю.

Таким образом, в широком смысле конические проекции заключают в себе все цилиндрические и азимутальные проекции, в том числе и перспективные, являющиеся частным случаем азимутальных.

Наряду с нормальными проекциями, представленными на рис. 4.2, 4.3, 4.4, 4.5, азимутальные, конические и цилиндрические проекции могут быть поперечными, когда для азимутальных проекций картинная плоскость касается глобуса на экваторе, а ось цилиндра или конуса лежит в плоскости экватора, как это показано на рис.4.6, и косыми, когда главный луч, ось конуса или цилиндра расположены относительно оси вращения под углом 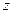, причем 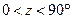, как это показано на рис.4.7.

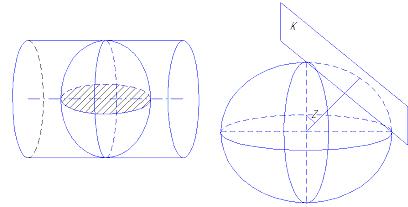
Рис.4.6 Рис. 4.7

До сих пор мы рассматривали касательные проекции. Это азимутальные проекции, касающиеся глобуса в точке касания (рис.4.3, 4.7), нормальные конические и цилиндрические проекции, касающиеся глобуса по параллели касания, в т.ч. по экватору (рис. 4.2, 4.5) и поперечно-цилиндрические проекции, касающиеся глобуса по меридиану касания (рис. 4.6).

Однако, перечисленные выше проекции могут быть также секущими проекциями, когда картинная плоскость пересекает глобус по параллели в азимутальной проекции, а конус или цилиндр пересекают глобус по двум параллелям, которые называют параллелями сечения в конической и цилиндрической проекции, как это показано на рис. 4.8.

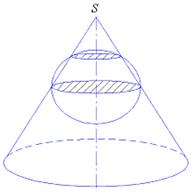
Рис. 4.8

Кроме перечисленных выше проекций для мелкомасштабного картографирования принимают ещё несколько видов проекций, в т.ч:

Дата добавления: 2015-06-04