Линейное программирование

Допустим, дана система т линейно независимых уравнений с n неизвестными x₁,…, х_п, называемая системой ограниче­ний задачи линейного программирования:

Характерной особенностью данной задачи является то, что число уравнений меньше числа неизвестных, т. е. m<n. Требуется найти неотрицательные значения пере­менных , которые удовлетворяют урав­нениям ограничения и обращают в минимум целевую функцию

Иногда в задаче линейного программирования все или некоторые из уравнений имеют вид не­равенств. Так, вместо уравнения

в систему может входить неравенства вида

или

От таких неравенств легко перейти к урав­нениям, вводя добавочную переменную х_n+j³0 так, что­бы в зависимости от знака неравенства имело место одно из двух выражений

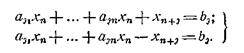
Поскольку число переменных п в этой системе больше числа уравнений т, то одно из возможных решений можно найти, если п — т каких-либо переменных положить равными нулю. Полученную при этом систему т уравнений с т неизвестными можно ре­шать обычными методами линейной алгебры. Правда, для того чтобы система т уравнений с т неизвестными имела решение, необходимо, чтобы определитель, составленный из коэффициентов при неизвестных, не обращался в нуль. Если это условие не выполняется, то можно приравнять нулю другие п — т переменных. Полученное при этом решение называется базисным решением.

Базисом называется любой набор т переменных, та­ких, что определитель, составленный из коэффициентов, при этих переменных не равен нулю. Эти т переменных называются базисными переменными (по отношению к данному базису). Остальные п — т переменных называются небазисными или свободными переменными В каж­дой конкретной системе уравнений может сущест­вовать несколько различных базисов с различными ба­зисными переменными.

Если положить все свободные переменные равными нулю и решить полученную систему т уравнений с т неизвестными, то получим базисное решение. Однако среди различных базисных решений будут такие, кото­рые дают отрицательные значения некоторых перемен­ных. Эти базисные решения противоречат условию зада­чи и являются недопустимыми.

Дата добавления: 2015-06-04