Итоговый баланс по народному хозяйству

Отрасль	Продукт	Итого
		…	m
	A11	A12	…	A1n	SjA1j
	A21	A22	…	A2n	SjA1j
…	…	…	…	…	…
n	An1	An2	…	Ann	SjAnj
Валовый выпуск	V1	V2	…	Vn	…
Конечное потребление	C1	C2	…	Cn	…

Задача расчета химической технологии. Пусть имеется N химических реакторов, соединенных последовательно и перерабатывающих некоторый тип сырья с целью выделить из него полезный продукт, и пусть х=(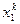, ,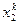…, 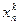) – характеристика свойств данного продукта. Обозначим x^k=(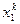, ,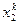…, 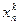) характеристику продукта на входе реактора k, тогда х^k+1 – характеристика на выходе из реактора. Пусть u^k – набор параметров, регулирующих процесс преобразования продукта в k -м реакторе. Считаем, что известна зависимость х^k+1=f_k(x^k,u^k) для k -го реактора. При этом на реактор могут быть наложены ограничения γ_k(u^k)<d_k. Требуется найти оптимальные векторы u^k, чтобы при заданных начальных свойствах х=(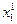, ,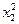…, 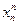) максимизировать величину φ(x¹,x²,…,x^N,u¹,u²,…,,u^N), которая может выражать, например, стоимость продукта.

Все приведенные пять задач являются задачами линейного программирования и приведены как полезные упражнения для адаптации прикладных задач к методам генетических вычислений.

Дополним данный список задач задачами конструкторского проектирования, которые можно поставить как оптимизационные. Это задачи компоновки, размещения и трассировки.

Задача компоновки. Процесс перехода от электрической схемы к конструктивному распределению (разбиению) всех элементов на группы, соответствующие конструктивам различных уровней, т. е. преобразование функционального описания аппаратуры в конструктивное, называется компоновкой. При компоновке элементы должны быть разбиты на микросхемы, типовые элементы замены (ТЭЗ), устройства, блоки, стойки. В задаче заданы функциональная электрическая схема, номенклатура модулей низшего уровня, типовые комбинации элементов, требуется покрыть исходную схему
модулями из заданного набора и минимизировать как число модулей, так и число типов модулей. На практике критерий оптимальности может быть сложным и включать в себя суммарную площадь, электромагнитную совместимость элементов в одном модуле, параметры теплообмена между элементами в узле.

Задача размещения. Размещение элементов — это определение их местоположения на коммутационном поле в конструктивном модуле, при котором создаются наилучшие условия для последующей трассировки. Задача размещения различается для однотипных, кратных и разногабаритных элементов. Критерии размещения могут быть следующими: суммарная длина всех соединений, расстояние между элементами, соединенными наибольшим количеством связей, число пересечений проводников, длина самых длинных связей, число цепей простой конфигурации, число перегибов проводников, число межслойных переходов, параметры паразитных связей, равномерность температуры на коммуникационном поле.

Задача трассировки монтажных соединений. Трассировка — это построение на монтажном поле всех цепей данного конструктива, координаты начал и концов которых определены при размещении всех элементов. На проведение трассировки
влияет технология монтажа элементов: проводной монтаж, печатный и пленочный монтаж и т. д. Критерии оптимальности трассировки для разных технологий монтажа приведена ниже.

Технология	Критерий
Проводной монтаж	Суммарная длина соединений, длина самой длинной связи
Многослойные печатные платы с металлизацией сквозных отверстий	Суммарная длина соединений, число переходных отверстий

Технология	Критерий
Многослойные печатные платы с открытыми контактными площадками и выступающими выводами	Суммарная длина соединений, число слоев
Интегральные схемы	Шаг металлизации, число межслойных переходов, число пересечений проводников

Задачи компоновки, размещения и трассировки носят исследовательский характер, применение для их решения генетических вычислений в случае конкретной технологии может оказаться сложной задачей.

Контрольные вопросы

1. Какую структуру хромосомы и способ ее кодирования можно предложить для задач: о диете, транспортной, рациональном использовании посевных площадей, межотраслевого баланса, расчета химической технологии, размещения, компоновки и трассировки монтажных соединений?

2. Какие проблемно-зависимые операторы кроссовера и мутации можно предложить для задач, перечисленных в первом вопросе к данной лабораторной работе?

3. Какие модели (аналитические или алгоритмические) можно предложить для формирования функций оптимальности данных задач?

[1] Например, plot(X,Y,' g+:') изображает точки зеленого цвета с помощью символа «+».

[2] Например, для четырех векторов (содержащих только одну 1 в каждой
строке) можно найти индексы единиц: vec = [ 1 0 0 0; 0 0 1 0; 0 1 0 1 ];ind = vec2ind(yec).

Дата добавления: 2015-06-04