Ньютоновская жидкость

ВЯЗКИЕ ЖИДКОСТИ

ОБЩИЕ СВЕДЕНИЯ О РЕОЛОГИЧЕСКИХ СВОЙСТВАХ ЖИДКОСТИ

Сложное внутреннее строение нефтей и нефтепродуктов обуслов­ливает большое разнообразие их реологического поведения. В связи с этим при. проектировании и эксплуатации трубопроводов возникает необходимость в детальном изучении реологических свойств перекачиваемых нефтей и нефтепродуктов. От того, насколько точно установлены природа, характер поведения и структурно-механические харак­теристики данной жидкости в конкретных температурных условиях, будет зависеть эффективность эксплуатации данного трубопровода.

Раздел науки, изучающий структурно-механические свойства разнообразных материалов (в том числе и жидкостей) в различных ре­жимах деформирования, когда одновременно проявляется их способность к течению и накоплению обратимых деформаций, называется реологией. Одной из главных задач реологии является установление связей между напряженным состоянием среды, деформациями и скоростями деформации. Уравнения, устанавливающие такую связь, назы­вают реологическими уравнениями состояния. Реологические уравне­ния состояния являются математическим отображением или математи­ки моделями реальных свойств среды.

Чтобы понять сущность происходящих явлений и механизм по­строения моделей, рассмотрим два физических понятия, связями деформацией среды. Если внешняя сила, воздействуя на жидкость, со­вершает работу, то эта работа может, во-первых, запасаться в струе, так что в объеме жидкости накапливается упругая энергия, во-вторых, работа внешних сил может необратимо рассеиваться (диссипировать).

Эти два явления позволяют классифицировать различных среды следующим образом. Если при деформации вся внешняя работа пере­ходит в упругую энергию, такая среда называется упругой. Если вся внешняя работа диссипирует, то среда называется вязкой.

Если внешняя работа частично переходит в упругую энергию, а частично диссипирует, то среду называют вязкоупругой.

Жидкости относятся к вязким и вязкоупругим средам.

Если в процессе деформирования среды вся работа внешних сил диссипирует, то это процесс течения в чистом виде, и после прекраще­ния действия внешних сил вся совершенная деформация оказывается необратимой, и достигнутое новое состояние будет равновесным. Ха­рактер процесса течения будет определяться связью напряжений, воз­никающих в жидкости, и скоростью деформации.

Простейшая реологическая модель вязкой жидкости была предложена Ньютоном. Она устанавливает линейную связь между каса-­
тельными напряжениями и градиентом скорости. Этой реологической
модели подчиняются многие нефти и нефтепродукты, содержащие небольшое количество парафинов и асфальто-смолистых веществ (бензины, дизельное топливо, некоторые сорта масел и мазутов, ряд нефтей при положительных температурах). Жидкости, подчиняющиеся реологической модели Ньютона (1). называются ньютоновскими жид­костями. К ньютоновским жидкостям также относятся и такие широко известные жидкости как вода, спирт, эфир и др.

где т - напряжение сил трения:

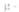коэффициент, характеризующий свойства данной жидкости:

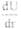градиент скорости сдвига по радиусу трубы ( 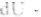скорость смещения одною слоя относительно другого. 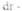расстояние между осями двух смежных слоев).

Коэффициент, характеризующий свойства жидкости и. получил название динамической вязкости.

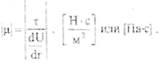
Часто динамическую вязкость выражают в пуазах [ Пз ]. Между размерностью динамической вязкости в системе СИ и пуазе шествует зависимость: 1 Па-с=10 Пз.

В практических расчетах часто применяют кинематическую вяз­кость ν, представляющую отношение динамической вязкости к плот­ности жидкости:

Размерность кинематической вязкости в системе СИ есть [м²/с]. Величина кинематической вязкости, равная 10-⁴ м*/с, получила назва­ние стоке [Ст], а равная 10'⁶ м²/с называется сантисгокс [сСт].

Способность жидкостей оказывать сопротивление, скольжению одного ее слоя относительно другого называется внутренним трением или вязкостью. В жидкостях передача количества движения при соуда­рении молекул несущественна, а вязкость, в основном, обусловлена действием силовых полей молекул, колеблющихся внутри регулярной структуры, в результате чего и происходит обмен количеством движе­ния. Так как вязкость жидкостей характеризует молекулярные взаимодействия частиц, то. естественно, она сильно зависит от температурь:. Экспериментально установлено, что при повышении температуры вяз­кость капельных жидкостей снижается (см. рис. 1).

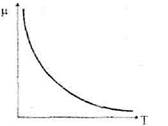
Рис. I. Зависимость вязкости жидкости от температуры

При расчетах технологических процессов с нефтями и нефтепро­дуктами лучше всего пользоваться табличными данными для вязкости. В тех случаях, когда экспериментальных данных по вязкости недостаточно пользоваться расчетными формулами зависимости вяз­кости от температуры, например, формулой Рейнольдса-Филонова

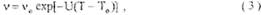ν₀- кинематическая вязкость при Т₀;

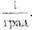U - коэффициент крутизны вискограммы,

График зависимости между напряжением и скоростью сдвига на­зывают "кривой течения". Для ньютоновских жидкостей "кривая тече­ния'' представляет собой прямую линию с тангенсом угла наклона а, равным и (рис. 2).

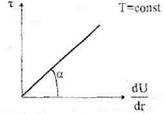
Рис. 2. Кривая течения ньютоновской жидкости

Дата добавления: 2015-06-04