Реология гелей

Реология – наука о течении и деформации материала.

Первоначально под термином реология подразумевалась классическая механика и эластичность потоков ньютоновских жидкостей, типа воды и малых деформаций твердых тел, типа стали и древесины.

Сейчас, практически, слово «реология» относят к течению и деформации «неклассических» материалов: резины, пластмасс, растворов полимеров, расплавов стекла, почвы и т.д.

Для изучения реологических характеристик гелей используют следующие параметры:

- напряжение сдвига, Па, гПа, ;

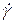- скорость сдвига (производная функции по времени), 1/с, ;

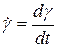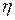- вязкость, Па^.с.

Между этими параметрами существует определенная взаимосвязь:

Эта формула является выражением закона Ньютона или закона течения идеальных вязких жидкостей.

На рис. 9.1 приведена схема, иллюстрирующая сдвиговое течение жидкости в ламинарном режиме.

Рис. 9.1. Схема сдвигового течения жидкости.

На основе этой схемы можно получить выражение для скорости сдвига .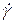

На рисунке приняты следующие обозначения:

х - расстояние между соседними движущимися слоями;

l- линейное смещение отдельного слоя за время t;

- скорость смещения слоя;

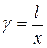- деформация сдвига;

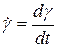- скорость деформации сдвига.

Из схемы следует, что градиент скорости 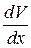равен скорости деформации: .

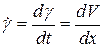Для идеальных жидкостей градиент скорости прямопропорционален напряжению сдвига:

Здесь 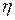- константа характеризующая силу трения между перемещающимися слоями жидкости, которая называется вязкостью.

Поскольку , можно записать:

Вязкость ньютоновских жидкостей постоянна, т.е. она не зависит от характеристик потока.

Для неньютоновских сред вязкость зависит от параметров течения, т.е. существуют зависимости:

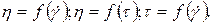
Эти зависимости принято называть реологическими кривыми или кривыми течения.

По форме реологические кривые неньютоновских систем делят на три группы:

- бингамовские (вязкопластичные среды);

- псевдопластичные;

- дилатантные.

Ниже на рис. 9.2 приведены кривые течения различных тел:

Рис. 9.2. Кривые течения различных тел:

1- ньютоновская жидкость;

2 – идеальнопластичное тело (тело Бингама – деформация по закону Ньютона после достижения некоторого предела сдвига ). Тела, имеющие определенную величину предела текучести, называются пластичными, а их деформации – пластическими;

3 – псевдопластическая система;

4 – дилатантная жидкость.

Реологические кривые перечисленных систем в первом приближении описываются следующими уравнениями:

ньютоновские среды –

бингамовские среды –

псевдопластические среды – 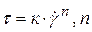<1® >0

дилатантные среды – 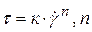<1® <0.

Вязкость псевдопластичных сред с ростом скорости сдвига уменьшается (тиксотропия), дилатантных сред, напротив, возрастает (реолексия).

Механизм явлений, который приводит к аномальному поведению жидкостей не всегда ясен. Поэтому для описания закономерностей деформации жидких систем применяют механические модели, составленные из простых механических элементов.

Для приготовления печатных красок используются системы, которые характеризуются псевдопластическим характером течения.

Полные реологические кривые таких систем имеют вид, показанный на рис. 9.3:

Рис. 9.3. Полные реологические кривые

псевдопластических сред.

Выбор логарифмических координат обусловлен тем, что в таком представлении наиболее важный участок (с наиболее интенсивным падением вязкости) имеет линейную форму.

Освальд-де-Вилл предложил для его описания уравнение степенного вида:

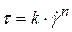
где 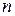- индекс течения.

Уравнением широко пользуются, так как оно позволяет графическим способом определить его коэффициенты.

Коэффициент 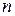равен тангенсу угла наклона прямой зависимости , а 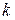равен расстоянию от начала координат до пересечения прямой, продлевающей реологическую кривую до ее пересечения с осью .

Дата добавления: 2015-06-04