Практическй пример последовательности расчетов по многокритериальному методу анализа иерархий (МАИ)

Допустим, что получены три альтернативных варианта производственной программы предприятия

1 этап. Поставим перед собой цель выбрать оптимальный вариант производственной программы предприятия.

2 этап. Определение состава критериев (параметров), которым должен удовлетворять наилучший вариант производственной программы предприятия:

1) объем валовой прибыли;

2) объем выпуска готовой продукции;

3) совокупная себестоимость, запланированной к выпуску продукции;

4) объем средств, связанных в запасах готовой продукции на складе;

5) уровень использования производственной мощности;

6) доля целевого рынка.

Как видим, задача выбора программы предприятия является многокритериальной.

3 этап. Представим данную проблему в виде иерархии (рис. 2).

Рис. 2. Декомпозиции задачи

Краткая характеристика вариантов:

Альтернатива производственная программа А. Данному варианту производственной программы соответствует хороший объем реализуемой продукции, приемлемая совокупная себестоимость запланированной к выпуску продукции, приемлемый объем средств, связанных в запасах готовой продукции на складе, неплохо используется производственная мощность предприятия, достаточна доля осваиваемого целевого рынка, но невысок объем получаемой прибыли.

Альтернатива производственная программа Б. Этому варианту производственной программы соответствует высокая прибыль, достаточно большой объем реализуемой продукции, сравнительно небольшой объем средств, связанных в запасах готовой продукции на складе, неплохо используется производственная мощность предприятия, но величина совокупной себестоимости запланированного к выпуску продукции неприемлема.

Альтернатива производственная программа В. Данному варианту производственной программы соответствует достаточна высокая прибыль, сравнительно низкая совокупная себестоимость запланированной к выпуску продукции, достаточно ограниченный объем средств, связанных в запасах готовой продукции на складе, неплохо используется производственная мощность предприятия, но невысокая доля осваиваемого целевого рынка.

Для проведения субъективных парных сравнений автором метода МАИ разработана наиболее подходящая для общего случая шкала. Содержание этой шкалы приведено в табл. 1.

Таблица 1

Шкала относительной важности сравниваемых элементов

Интенсивность относительной важности	Определение	Объяснения
	Равная важность	Равный вклад двух видов деятельности в цель
	Умеренное превосходство одного над другим	Опыт и суждения дают легкое превосходство одному виду деятельности над другим
	Существенное или сильное превосходство	Опыт и суждения дают сильное превосходство, что оно становится практически значительным
	Очень сильное превосходство	Очевидность одного вида деятельности над другим подтверждается наиболее сильно
2, 4, 6, 8	Промежуточные решения между двумя суждениями	Применяются в компромиссном случае
Обратные величины приведенных выше чисел	Если при сравнении одного вида деятельности с другим получено одно из вышеуказанных чисел (например, 3), то при сравнении второго вида деятельности с первым получим обратную величину (т.е. 1/3)	-

Эффективность использования приведенной выше шкалы доказана как теоретически, так и большим практическим опытом ее применения при решении многокритериальных задач в различных сферах бизнеса.

4 этап. Синтез приоритетов для 2-го уровня. На этом этапе представляется задача в виде иерархической структуры, составляется матрица и выражаются количественно субъективные парные суждения. Все приведенные в матрицах цифры означают нечто конкретное. На их основе надо выбрать наилучший вариант предприятия-аналога, у которого числовые оценки исследуемых критериев представлены наиболее полно.

На основании изложенной выше информации и шкалы относительно важности сравниваемых критериев (параметров) заполним числовыми характеристиками матрицу попарных сравнений для уровня 2 (табл. 2).

Таблица 2

Выбор наилучшего варианта: матрица попарных сравнений для уровня 2

Критерии
	1/2					1/2
	1/3	1/4
	1/5	1/7	1/7			1/8
	1/4	1/8	1/5	1/4		1/6
	1/2		1/3

5 этап. Синтез: локальные приоритеты 2–го уровня. Из группы матриц парных сравнений формируем набор локальных приоритетов, которые выражают относительное влияние множества элементов на элемент примыкающего сверху уровня. Находим относительную величину, ценность или вероятность каждого отдельного объекта через "решение" матриц, каждая из которых обладает обратно симметричными свойствами. Для этого нужно вычислить множество собственных векторов для каждой матрицы, а затем нормализовать (привести к безразмерному виду) результат, получая тем самым вектор приоритетов.

Вычисление собственных векторов это сложная задача. Одним из наилучших способов является определение геометрической средней. Это можно сделать, перемножая элементы в каждой строке и извлекая корни n-й степени, где n число элементов. Полученный таким образом столбец чисел нормализуется путем деления каждого числа на сумму всех чисел.

После того, как компоненты собственного вектора получены для всех n строк, становится возможным их использование для дальнейших вычислений.

Следующий этап вычислений связан с нормализацией с целью получение соответствующих оценок вектора приоритетов.

5.1. Находим величину приоритета для каждой строки матрицы:

для первой строки:

Таблица 3

Выбор наилучшего варианта: матрица попарных сравнений для уровня 2

Критерии							Произведение элементов строк	Вектор Приоритетов Рi
								2,493
	1/2					1/2		1,963
	1/3	1/4					8,6625	1,433
	1/5	1/7	1/7			1/8	0,00196	0,354
	1/4	1/8	1/5	1/4		1/6	0,00027	0,254
	1/2		1/3				15,84	1,585
Сумма	2,78	5,515	8,67	28,25		6,795		8,082

По первой строке: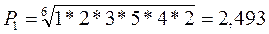

По второй строке: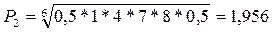

и ; ; ; .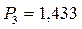

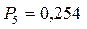5.2. Нормализация локальных приоритетов (приведение к безразмерному виду):

Осуществим процедуру нормализации вектора приоритетов. Информация, полученная расчетным путем, отражена в табл. 4.

Таблица 4

Выбор лучшего варианта: матрица попарных сравнений для уровня 2

Критерии							Вектор приоритетов	Оценка нормализованного вектора
							2,493	0,309
	1/2					1/2	1,963	0,242
	1/3	1/4					1,433	0,177
	1/5	1/7	1/7			1/8	0,354	0,044
	1/4	1/8	1/5	1/4		1/6	0,254	0,031
	1/2		1/3				1,585	0,196
Сумма	2,78	5,515	8,67	28,25		6,795	8,082	1,000

На последующем этапе предусмотрена проверка уровня согласованности локальных приоритетов.

Определяем наибольшее значение матрицы суждений. Для этого сумму первого столбца умножаем на величину первой компоненты нормализованного вектора приоритетов, сумма второго столбца умножается на вторую компоненту нормализованного вектора приоритетов и т.д.

В нашем случае наибольшее собственное значение матрицы суждений будет равно:

6 этап. Согласованность локальных приоритетов. Важным элементом расчетов по МАИ является определение так называемого индекса согласованности (ИС). Он дает информацию о степени нарушения численной (кардинально) и транзитивной (порядковой) согласованности.

Индекс согласованности в каждой матрице и для всей иерархии может быть приближенно получен вычислениями вручную.

Порядок его определения заключается в следующем. Сначала проводится суммирование элементов по каждому столбцу, затем сумма первого столбца умножается на величину первой компоненты нормализованного вектора приоритетов, сумма второго столбца на вторую компоненту и т.д. Полученные числа суммируются. Таким образом, можно получить величину, которую обозначим как L_max.

Формула индекса согласованности (ИС) выглядит так;

ИС =(Lmax - n)/(n - 1),

где n - количество сравниваемых элементов (оно равно числу критериев оптимальности).

Далее сравним каждую полученную величину с той, которая получилась бы при случайном выборе количественных суждений из шкалы 1/9; 1/8; 1/7,..., 1; 2,..., 9, но при образовании обратно симметричной матрицы. Автором МАИ рекомендуются следующие средние согласованности для случайных матриц разного порядка (т.е. n):

Размер матрицы
Случайная согласованность			0,58	0,9	1,12	1,24	1,32	1,41	1,45	1,49

Если разделить ИС на число, соответствующее случайной согласованности матрицы того же порядка, получим отношение согласованности (ОС). Величина ОС не должна быть более 20%. Если ОС выходит за эти пределы, то ЛПР нужно заново исследовать содержательную ее сторону и соответствующие количественные оценки элементов и внести необходимые изменения в исходные данные.

Вычислим собственное значение индекса согласованности и отношение согласованности.

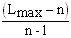Определим численное значение индекса согласованности (ИС):

ИС =,

где n -число сравниваемых элементов.

В нашем случае получим ИС = (7,172 - 6): 5 = 0,234.

Определим отношение согласованности (ОС) элементов матрицы. Для этого воспользуемся средними согласованиями для случайных матриц разного порядка.

Размер матрицы
Случайная согласованность, α			0,58	0,9	1,12	1,24	1,32	1,41	1,45	1,49

В нашем случае отношение согласованности составит:

ОС = ИС: α = 0,234: 1,24 = 0,19 (т.е. 19%).

Величина ОС не должна быть более 20%. Если ОС выходит за эти пределы, то необходимо заново исследовать содержательную ее сторону и соответствующие количественные оценки элементов и внести необходимые изменения в исходные данные.

7 этап. Синтез приоритетов для 3-го уровня. В отношении матрицы попарных сравнений для уровня 3 вычислим векторы приоритетов, наибольшее собственное значение матрицы суждений, индекс согласованности (ИС) и отношение согласованности (ОС).

Таблица 5

Результаты расчетов по матрице попарных сравнений для уровня 3

Критерий 1	А	Б	В	Вектор приоритетов	Критерий 2	А	Б	В	Вектор приоритетов
А		1/3	1/5	0,104	А		1/4	1/5	0,082
Б			1/3	0,258	Б			1/7	0,184
В				0,638	В				0,733
Сумма:		4,33	1,53	Lmax = = 3,061	Сумма:		8,25	1,34	Lmax = = 3,12
				ИС=0,03					ИС=0,06
				ОС=0,05					ОС=0,103
Критерий 3	А	Б	В	Вектор приоритетов	Критерий 4	А	Б	В	Вектор приоритетов
А		1/7	1/5	0,091	А		1/3	1/5	0,14
Б				0,671	Б				0,585
В		1/4		0,238	В		1/4		0,275
Сумма:		1,39	5,5	Lmax = = 3,16	Сумма:		1,58	5,5	Lmax = = 3,217
				ИС=0,08					ИС=0,109
				ОС=0,14					ОС=0,19
Критерий 5	А	Б	В	Вектор приоритетов	Критерий 6	А	Б	В	Вектор приоритетов
А		1/4	1/3	1,114	А		1/3	1/4	0,108
Б			1/5	0,242	Б			1/5	0,211
В				0,644	В				0,679
Сумма		6,25	1,53	Lmax = = 3,201	Сумма		6,35	1,45	Lmax = = 3,187
				ИС=0,1					ИС=0,09
				ОС=0,17					ОС=0,16

Дата добавления: 2015-06-04