
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Оптика. 5 страница
|
|
|
|
I φ=AφAφ*=I0(sinu/u)2(sin N δ/sinδ)2. Первый множ – дифр.член, второй – инт. 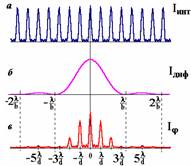
18. см.13.
- Принцип Г-Фр. не позв.получить выр.для коэфф.К(χ), входящего в инт.Фр.
- Фаза волны, прих.в т.набл.в отсутствии преп, отличается на π/2 от фазы волны, идущей от вторич.ист., расп.строго на оси (сравнить OO ∞ и начальный малый вектор сп, вых.из т. О).
Эти вопр.решаются в теории дифр.Кирх, основ.на преобр. волнового ур-я с заданными условиями на границе в ур-е Гельмгольца для компл.ампл.(не зависящей от времени). Исп.интегральная теорема Кирх-Гельм, позв.найти поле в нек.т. Р, если известна компл.ампл.поля и ее произв.по нормали на какой либо пов-и, охватывающей точку Р.
Т.е. в теории Фр в кач-ве втор.ист.берутся т.замкнутой пов-ти, окружающей ист.изл. В теории Кирх.напротив: пов-ть втор.ист-ков окружает т.набл. В результ. преобр.можно получить дифр.интеграл Фр-Кирх:
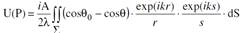
θ0 и θ – углы, обр.векторами r и s с нормалью к пл-ти отверстия. Т.о. K(θ0,θ)=i/2λ (cos θ0 – cosθ). (а из сообр.спирали Фр было получ.K0=i/λ, что соотв. значению K(θ0,θ) при θ0=0 и θ=π.
19. Пусть расст.от ист.до пл-ти объекта и от этой пл-ти до экрана
равны a и b. Если хар.размер объекта << a и b, то можно положить θ0≈0, θ≈π, 1/r≈1/a, 1/s≈1/b. Интеграл Фр–Кирх:
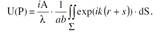
Введем в пл-ти объекта сист.коорд.{ x, y }, в пл-ти экр.{x’, y’}. Для r и s:
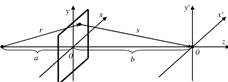
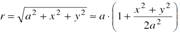
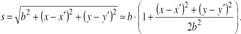
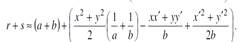
Инт-ие по x и y, поэтому под ∫ останется
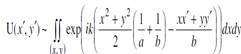
- прибл.Френеля.
Первым слаг.под exp можно пренебр, если
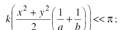
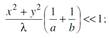
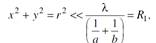
R1 – 1 з.Фр. Т.о. если для пл.набл.размеры объекта < размеров1 з.Фр. то инт.Фр-Кирх:
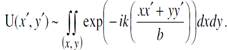
- прибл.Фраунгоф.
Этот инт. – простр.преобр.Фурье по простр.частотам: kx=kx/b≈ksinφх, ky=..., φ- угол дифр.
Дифр.на 1щ: пл.волна=> во всех точках Σ ампл.одинак U0. Лучи от вт.ист.под углом φ к перв. напр, соб.в фок.пл-ти линзы в Nφ. Вклад от эл-та dх: 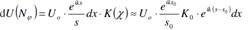
где (s-s0)=xsinφ– разн.хода м|у лучом из т.щели с коорд.х, и лучом из центра щели.
Результ.поле:
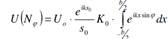
Ф-я проп: α(х,у) – отн.ампл.поля Е2(х,у) пад.волны в т.за преп.к компл.ампл.поля Е1(х,у) перед преп. Для щели α(х,у)={1 |x|<b/2; 0 |x|>b/2. тогда
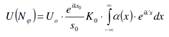 (в эксп. k ’)
(в эксп. k ’)
это пр.преобр.Фурье от ф.проп.препятствия, k’=ksinφ- простр.частота. Т.о.дифр.Фраунг – простр.разложение огранич.света на плоские волны.
Для дифр.Фраунг. ε(θ)= (i+1)/√(2λb) e-ikb∫-∞∞ε0(x)eikxsinθdx – это простр.инт.Фурье, ksinθ – простр.частота. ε(р)= (i+1)/√(2λb)e-ikbε0(kx), где ε0(kx)= ∫-∞∞ε0(x)exp[ikxx]dx - протр.спектр.амплитуда. I(p)=c/8π |ε(D)|2= c/8π 1/λb S0(kx). S0(kx)= |ε0(kx)|2 – простр.сп.пл-ть или угловой спектр излучения. Физ смысл Фраунг.дифр: пространственное разложение ограниченного св.пучка на плоские волны.
В сдуч.плоской волны (1/a→0) для расст.b, при кот.прибл.Фр.перех в прибл.Фраунг: b<<r2/λ=bдифр – дифр.длина. По этой длине пров.граница м/у дифр.Фр. и Фраунг.
А если a и b близки к разм.объекта – геом.оптика.

20. Дифр.реш. – простр.периодич.структура, сост.из большого числа одинак.по ширине щелей, нах.на одинак расст.друг от друга. Распр.поля: I φ=I0(sinu/u)2(sin N δ/sinδ)2, u= kbSinφ/2, δ=kdSinφ/2. Главные макс.нах из усл δ=0,π, 2π, πm или dsinφ=0, λ,mλ, инт.член (с δ) →N2 – это дифр.макс.m-ого пор. Ближайшие к ним мин.нах из simNδ=0 или dsinφm,min= (m±1/N)λ. (sinφ≈φ, Δφm – угл.размер макс. Надо взять d() при пост d и λ. Δφm = λ/Ndcosφm= λ/Dcosφm, D – ширина реш. (cosφm=1 =>...)
dsinφm= mλ => макс.всех пор.для различ.длин волн соотв.свой угол дифр sinφm(λ)=… => это спектр.прибор(простр.разлож.света на монохр.сост).
Главн.дифр мин – при nλ/b, а инт - nλ/d (?)
Различают ампл.и фаз.д.р. У ампл.периодически изм.коэфф.отражения или пропускания, что вызывает изм.ампл.пад.волны (реш.из щелей в непрозр). У фаз.д.р. штрихам придаётся спец.форма, к-рая периодич.изм.фазу волны. Наим.потери света.
(рис из лекции)
21. 2D периодич.структ. м/б получ.путем наложения 2 скрещ.дифр.р. Если щели 1реш. _|_ щелям другой, то получ.прямоуг.стуктура. Вид дифр.картины, возн.при дифр.лазерного пучка на скрещ.реш.

1 дифр.реш, штрихи кот.вертик, разворачивает лаз.луч в веер лучей, леж.в гориз.пл-ти. 2 реш, штрихи кот.гориз, каждый из пад.на нее лучей разв. в веер в вертик.пл-ти => 2D дифр.картина.
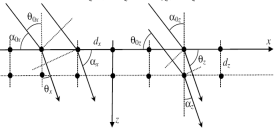
Ид.крист. - регулярная 3D периодич.структ. с хар.d~1 Ангстрема. Свет вид.диап. не проходит, но для рент.лучей с λ≤d - дифракция. Крист.с элем. яч.в форме прямоуг. пар-да с разм. dx, dy, dz. Атомы становятся вторич.ист.когер.изл. Усл диф. макс:
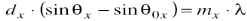
Аналогич.для y и z. В 3D напр.луча задают углом, образованным этим лучом с соотв.
осью коорд:
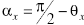
синус превратится в кос.
Ур-я Лауэ:
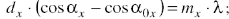
Аналог.для y и z
Соотн. м/у направляющими косинусами:
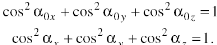
mx, my, mz целые => для произвольной λ невозм.удовлетворить всем ур-ям. Поэтому при освещ.непр.спектром ч/з кристалл пройдет изл.только на неск.λ. Т.е. 3D структ как узкополосный фильтр.
Дифр. в отр.свете. Атомы- параллел. плос-ти,
на одинак.расст. друг от друга. Возн.инт-я. Формула для Δs такая же, как при инт-ии в плоскопар.пл, усл.наблюдения
макс.(усл. Брэгга-Вульфа):
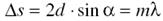
(косинус превр. в синус, т.к. задается угол скольжения)
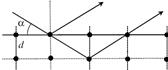
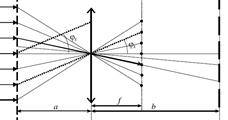
Схема Аббе-Портера. Плоская волна падает нормально на объект, нах.на расст. а от соб.линзы с фок.расст.f. Экран для наблюд. установлен в плоскости, сопряженной с плоскостью объекта, т.е. на расстоянии b, удовлетворяющем формуле тонкой линзы. На экране изобр. переверн. увел. в b/a раз.Введем функцию пропускания объекта τ(x,y)=A(x,y)/А0(х,у), А(х, у)- компл.ампл. поля сразу после прохождения объекта, А0(х, у)- ампл. поля пад.волны в пл-ти объекта. Положим А0(х, у) ≡1, a=b=2f и будем считать, что объект.симм.отн поворота на 180º.
Распр.амплитуды изображения на экране Aизобр(x,y)= A(x,у)= τ(x,y).
После прохождения объекта формируется простр-ный фурье-спектр (анализ) функции (след. из приближ Фраунг.) пропускания объекта по пространств. частотам kx и ky:
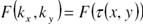
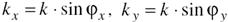
Линза локализует полученный спектр в своей фок.пл-ти.
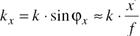
x’- коорд.а в фок пл-ти. вследствие конечного радиуса R линзы пространственные частоты, соотв.углам tgφx≥R/a не попадут в линзу, и будут отсутствовать в фок.плоскости. Это может привести к потере информации о мелких деталях в изображении.
Если никаких преобразований в фокальной плоскости не производить, то при свободном распространении в области пространства между фокальной плоскостью и плоскостью изображения осуществляется обратное фурье-преобразование (синтез), в результате формируется изображение, подобное исходному.
Если τ(x, y) - регулярная функция (например, дифр решетка), то в фокальной плоскости будет наблюдаться ряд ярких точек – дифр.максимумов. Перекрывая различ. максимумы, можно осуществлять преобразование пространственного спектра=>преобразование изображения.
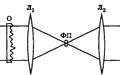
Метод темного поля. Метод темного поля используют в микроскопии для наблюдения структуры слабо поглощающих свет объектов (срезы живых тканей, клетки). Свет от источника проходит через исследуемый объект и линзу. В точке фокуса расположен небольшой непрозрачный диск Д. Линза проецирует изображение на экран. В отсутствие диска Д на экране видно светлое поле с почти однородной засветкой. При внесении диска освещенность экрана резко уменьшается — возникает "темное поле". При этом на темном фоне становится отчетливо видной структура объекта. Объяснение:. Неоднородная оптическая плотность или толщина прозрачного объекта вызывает преломление света и появление отклоненных лучей, Эти лучи, несущие информацию о структуре объекта и являющиеся полезным сигналом, пропускаются диском Д, размер которого достаточно мал. В то же время прямые лучи, которые не несут информации об объекте и являются помехой, задерживаются диском Д. Это и приводит к улучшению видности структуры объекта.
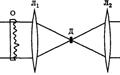
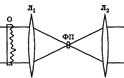
Метод фазового контраста. Используют в микроскопии для получения изображений прозрачных и бесцветных объектов. Неоднородность показателя преломления объекта, (живой клетки), приводит к тому, что прошедшая через объект световая волна претерпевает в разных точках объекта разные изменения фазы, т. е. приобретает фазовый рельеф. В методе фазового контраста этот рельеф преобразуется в изменения яркости света — амплитудный рельеф — с помощью специальной фазовой пластинки, расположенной вблизи заднего фокуса объектива микроскопа. Схема подобна схеме, используемой в методе темного поля, только вместо непрозрачного диска в фокальной плоскости линзы расположен стеклянный диск — фазовая пластина. Она осущ. изменение фазы на π/2.
На пластину падает свет, не претерпевший преломления в объекте. Этот свет, не несущий информации о структуре объекта, линза собирает в точке фокуса. В то же время преломленные объектом лучи — полезный сигнал — минуют фазовую пластину, проходя сбоку от нее. Затем фоновая волна, фаза которой сдвинута на π/2, и сигнальная волна интерферируют, в результате чего формируется изображение структуры объекта.
Пусть объект характер. комплексн. функц. пропускания 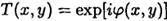
где φ(x, у) — действительная функция, модуль которой <<1. Можем приближ написать 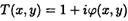 .Комлекс. амплит. пад. волны
.Комлекс. амплит. пад. волны 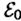 . Тогда прошедшая
. Тогда прошедшая
имеет амлитуду 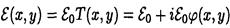 **
**
При отсутсвии пластинки расперд. интенсивности 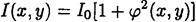
Структура просматрив плохо. Иное если поставить фаз пластнику π/2. В формуле ** первое слаг 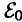 , преврат в
, преврат в 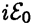 .
.
Тогда расперд. интенсивности 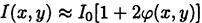
Видим что при наличии фазовой пластинки контрастность должна возрасти.
23. Дифр.реш. – простр.периодич.структура, сост.из большого числа одинак.по ширине щелей, нах.на одинак расст.друг от друга. Распр.поля: I φ=I0(sinu/u)2(sin N δ/sinδ)2, u= kbSinφ/2, δ=kdSinφ/2. Главные макс.нах из усл δ=0,π, 2π, πm или dsinφ=0, λ,mλ, инт.член (с δ) →N2 – это дифр.макс.m-ого пор. Ближайшие к ним мин.нах из simNδ=0 или dsinφm,min= (m±1/N)λ. (sinφ≈φ, Δφm – угл.размер макс. Надо взять d() при пост d и λ. Δφm = λ/Ndcosφm= λ/Dcosφm, D – ширина реш. (cosφm=1 =>...)
dsinφm= mλ => макс.всех пор.для различ.длин волн соотв.свой угол дифр sinφm(λ)=… => это спектр.прибор(простр.разлож.света на монохр.сост).
Главн.дифр мин – при nλ/b, а инт - nλ/d (?)
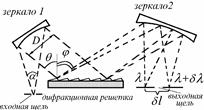
Вх щель находится в фокусе сф зеркала 1, явл коллиматорным объективом, который формирует паралл пучок лучей, падающих на диспергирующий элемент - дифр решетку. Если плоская волна падает на решетку под углом θ, то, вследствие дифр, максимумы инт-ти отраженного света с λ будут наблюдаться при углах φ соотв условию: d(sinθ – sinφ)=mλ, d- период реш.
Т.е если лучи с λ отраж от реш под углом φ, то лучи с λ+δλ отраж под углом φ+δφ. Сф зеркало 2 (камерный объектив) фокусирует паралл пучки лучей, идущие под разными углами, в разных
т.фок.пл-ти.
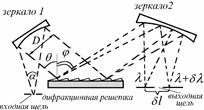
Угловая дисперсия. Dφ=dφm/dλ. Отношение угла, на кот разнесены лучи с λ-ми, отличающимися на dλ, к величине dλ. Можно найти, взяв d() от dsinφm=mλ по φm и λ. Dφ=dφm/dλ = m/dcosφm≈m/d.
Разрешающая способность. R=λ/δλ - отн λ излучения к δλ - наим разности длин волн двух спектр линий, при которой эти линии различимы, т.е. наблюдаются раздельно.
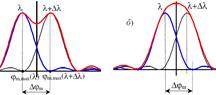
Крит.Релея: λ и Δλ разрешены, если угловое расстояние м/у главными макс.одного и того же порядка для этих λ не меньше угл ширины Δφm главного макс: φm, max(λ+Δλ) - φm, max(λ) ≥ Δφm, т.е в предельном случ макс m-го порядка для длины волны (λ+Δλ) совпадает с миним, ближайшим к макс того же порядка для длины волны λ, т.е. φm, max(λ+Δλ)=φm, min(λ). Отсюда получаем
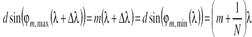
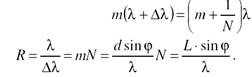
Свободная область дисперсии Δλ – макс ширина спектр интервала, при кот спектры соседних порядков не перекрываются. Т.е m-ый порядок для длины волны λ+Δλ совп с (m+1)-ым порядком для длины волны λ: m(λ+Δλ)=(m+1)λ, Δλ= λ/m.
Для дифр реш своб область дисперсии велика (в 1-м порядке дифр совпадает с λ). Обычно в дифр спектр приборе работают именно в 1-м порядке, т.к. в больших порядках, хотя и увелич разр.способность, но падает инт-ть макс за счет дифракц члена в формуле для Nщелей.
24. Спектр приборы осущ разложение изл на монохр составляющие, что дает возможность измерения распр энергии исследуемого излучения по частотам (длинам волн) т.е. определение спектра. Их основным узлом явл диспергирующий эл-т, который осущ. пространственное разделение излуч. разных λ.
Сп.приборы: дифракционные, призменные (исп зав-ть пок.преломления материала призмы от λ) и интерференционные (интерферометр Фабри-Перо).
Поведение инт-ра Фабри-Перо опис.формулами Эйри,
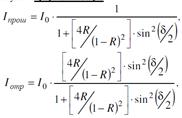
в которых разн.фаз м/у соседними лучами задается соотн. δ=kΔs=2hkncosθ. В случае конструкции ИФП как воздушной (n=1) прослойки толщиной hм/у зеркалами с коэфф отражения R имеем: δ=2hkcosθ. Усл макс для прошедшей инт-ти имеет вид: δ=2πm (m=0,1,2,…). Откуда 2hcosθm=mλ.
Для угловой дисперсии Dθ=dθm/dλ= m/2hsinθm.
ИФП обладает очень высокой разр.cпособностью. Из формул Эйри можно показать что R=λ/δλ=mF, где F=π√(ρ)/(1–ρ) - резкость инт.полос. R может достигать ~ 105 - 106. Разр.спос. можно повысить, увеличивая базу инт-ра (расстояние h между пластинами) и коэфф отражения зеркал.
Угл.ширина дифр.макс:
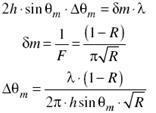
Своб.обл.дисперсии:
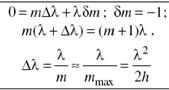
(ИФП рис.из прака)
25. Голография. В обычной фотогр на фотопластинке фиксируется только часть информации о световом поле, а именно пространственное распр инт-ти света. Информация о простр.распр.фазы поля теряется. Чтобы сохранить информацию об ампл. и о фазе: способ записи волновых полей - голография.
Заключается в том, чтобы фотографировать не само световое поле, идущее от объекта, а картину инт-ии этого поля с когерентной опорной волной. Картина инт-ии предметной и опорной волн, записанная на фотопластинку, называется голограммой. Т.к вид инт. картины зависит не только от ампл., но и от фаз инт-щих полей, на голограмме оказывается записанной вся информация о предметной волне — и ампл, и фаза поля. Для восст.предметной волны достаточно просветить голограмму опорной.
Для получения голограммы когерентный лазерный пучок делится на 2 части. Один пучок ("сигнальный") освещает объект, а другой пучок ("опорный") падает непосредственно на фотопластинку. Свет, отраженный объектом, образует "объектный" пучок, который также направляется на фотопластинку, где инт-т с опорной волной. Картина интерференции записывается на фотопластинку и после проявления образует голограмму.
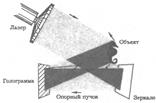
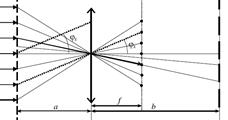
Схема Аббе-Портера. Плоская волна падает нормально на объект, нах.на расст. а от соб.линзы с фок.расст.f. Экран для наблюд. установлен в плоскости, сопряженной с плоскостью объекта, т.е. на расстоянии b, удовлетворяющем формуле тонкой линзы. На экране изобр. переверн. увел. в b/a раз.Введем функцию пропускания объекта τ(x,y)=A(x,y)/А0(х,у), А(х, у)- компл.ампл. поля сразу после прохождения объекта, А0(х, у)- ампл. поля пад.волны в пл-ти объекта. Положим А0(х, у) ≡1, a=b=2f и будем считать, что объект.симм.отн поворота на 180º.
Распр.амплитуды изображения на экране Aизобр(x,y)= A(x,у)= τ(x,y).
После прохождения объекта формируется простр-ный фурье-спектр (анализ) функции (след. из приближ Фраунг.) пропускания объекта по пространств. частотам kx и ky:
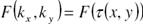
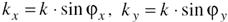
Линза локализует полученный спектр в своей фок.пл-ти.
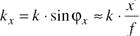
x’- коорд.а в фок пл-ти. вследствие конечного радиуса R линзы пространственные частоты, соотв.углам tgφx≥R/a не попадут в линзу, и будут отсутствовать в фок.плоскости. Это может привести к потере информации о мелких деталях в изображении.
Если никаких преобразований в фокальной плоскости не производить, то при свободном распространении в области пространства между фокальной плоскостью и плоскостью изображения осуществляется обратное фурье-преобразование (синтез), в результате формируется изображение, подобное исходному.
Если τ(x, y) - регулярная функция (например, дифр решетка), то в фокальной плоскости будет наблюдаться ряд ярких точек – дифр.максимумов. Перекрывая различ. максимумы, можно осуществлять преобразование пространственного спектра=>преобразование изображения.
Метод темного поля. Метод темного поля используют в микроскопии для наблюдения структуры слабо поглощающих свет объектов (срезы живых тканей, клетки). Свет от источника проходит через исследуемый объект и линзу. В точке фокуса расположен небольшой непрозрачный диск Д. Линза проецирует изображение на экран. В отсутствие диска Д на экране видно светлое поле с почти однородной засветкой. При внесении диска освещенность экрана резко уменьшается — возникает "темное поле". При этом на темном фоне становится отчетливо видной структура объекта. Объяснение:. Неоднородная оптическая плотность или толщина прозрачного объекта вызывает преломление света и появление отклоненных лучей, Эти лучи, несущие информацию о структуре объекта и являющиеся полезным сигналом, пропускаются диском Д, размер которого достаточно мал. В то же время прямые лучи, которые не несут информации об объекте и являются помехой, задерживаются диском Д. Это и приводит к улучшению видности структуры объекта.
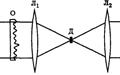
Метод фазового контраста. Используют в микроскопии для получения изображений прозрачных и бесцветных объектов. Неоднородность показателя преломления объекта, (живой клетки), приводит к тому, что прошедшая через объект световая волна претерпевает в разных точках объекта разные изменения фазы, т. е. приобретает фазовый рельеф. В методе фазового контраста этот рельеф преобразуется в изменения яркости света — амплитудный рельеф — с помощью специальной фазовой пластинки, расположенной вблизи заднего фокуса объектива микроскопа. Схема подобна схеме, используемой в методе темного поля, только вместо непрозрачного диска в фокальной плоскости линзы расположен стеклянный диск — фазовая пластина. Она осущ. изменение фазы на π/2.
На пластину падает свет, не претерпевший преломления в объекте. Этот свет, не несущий информации о структуре объекта, линза собирает в точке фокуса. В то же время преломленные объектом лучи — полезный сигнал — минуют фазовую пластину, проходя сбоку от нее. Затем фоновая волна, фаза которой сдвинута на π/2, и сигнальная волна интерферируют, в результате чего формируется изображение структуры объекта.
Пусть объект характер. комплексн. функц. пропускания 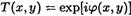
где φ(x, у) — действительная функция, модуль которой <<1. Можем приближ написать 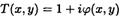 .Комлекс. амплит. пад. волны
.Комлекс. амплит. пад. волны 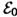 . Тогда прошедшая
. Тогда прошедшая
имеет амлитуду 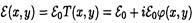 **
**
При отсутсвии пластинки расперд. интенсивности 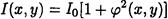
Структура просматрив плохо. Иное если поставить фаз пластнику π/2. В формуле ** первое слаг 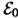 , преврат в
, преврат в 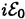 .
.
Тогда расперд. интенсивности 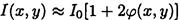
Видим что при наличии фазовой пластинки контрастность должна возрасти.
23. Дифр.реш. – простр.периодич.структура, сост.из большого числа одинак.по ширине щелей, нах.на одинак расст.друг от друга. Распр.поля: I φ=I0(sinu/u)2(sin N δ/sinδ)2, u= kbSinφ/2, δ=kdSinφ/2. Главные макс.нах из усл δ=0,π, 2π, πm или dsinφ=0, λ,mλ, инт.член (с δ) →N2 – это дифр.макс.m-ого пор. Ближайшие к ним мин.нах из simNδ=0 или dsinφm,min= (m±1/N)λ. (sinφ≈φ, Δφm – угл.размер макс. Надо взять d() при пост d и λ. Δφm = λ/Ndcosφm= λ/Dcosφm, D – ширина реш. (cosφm=1 =>...)
dsinφm= mλ => макс.всех пор.для различ.длин волн соотв.свой угол дифр sinφm(λ)=… => это спектр.прибор(простр.разлож.света на монохр.сост).
Главн.дифр мин – при nλ/b, а инт - nλ/d (?)
Вх щель находится в фокусе сф зеркала 1, явл коллиматорным объективом, который формирует паралл пучок лучей, падающих на диспергирующий элемент - дифр решетку. Если плоская волна падает на решетку под углом θ, то, вследствие дифр, максимумы инт-ти отраженного света с λ будут наблюдаться при углах φ соотв условию: d(sinθ – sinφ)=mλ, d- период реш.
Т.е если лучи с λ отраж от реш под углом φ, то лучи с λ+δλ отраж под углом φ+δφ. Сф зеркало 2 (камерный объектив) фокусирует паралл пучки лучей, идущие под разными углами, в разных
т.фок.пл-ти.
Угловая дисперсия. Dφ=dφm/dλ. Отношение угла, на кот разнесены лучи с λ-ми, отличающимися на dλ, к величине dλ. Можно найти, взяв d() от dsinφm=mλ по φm и λ. Dφ=dφm/dλ = m/dcosφm≈m/d.
Разрешающая способность. R=λ/δλ - отн λ излучения к δλ - наим разности длин волн двух спектр линий, при которой эти линии различимы, т.е. наблюдаются раздельно.
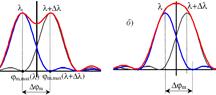
Крит.Релея: λ и Δλ разрешены, если угловое расстояние м/у главными макс.одного и того же порядка для этих λ не меньше угл ширины Δφm главного макс: φm, max(λ+Δλ) - φm, max(λ) ≥ Δφm, т.е в предельном случ макс m-го порядка для длины волны (λ+Δλ) совпадает с миним, ближайшим к макс того же порядка для длины волны λ, т.е. φm, max(λ+Δλ)=φm, min(λ). Отсюда получаем
|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 402; Нарушение авторских прав?; Мы поможем в написании вашей работы!