Квантовая физика - 2011

Схема и формула Бернулли.

На рисунке ниже мы можем увидеть схему диференциатора ОП, лицевую панель генератора и показ работы схемы

Формулы произведения тригонометрических функций

Формулы суммы и разности тригонометрических функций

Формулы понижения степени

Формулы половинного аргумента

Формулы двойного аргумента

Формулы сложения и вычитания

;

;

;

;

;

;

;

;

;

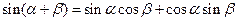
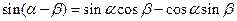
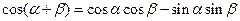
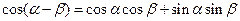
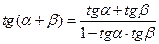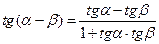
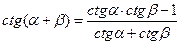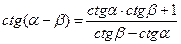
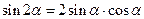
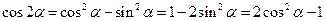
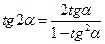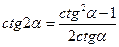
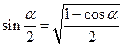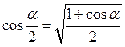
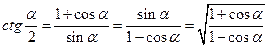
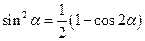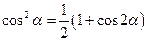
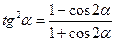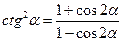
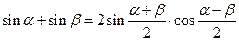
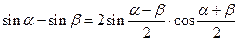
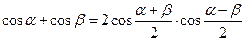
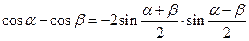
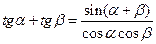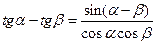
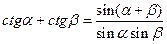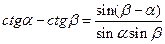
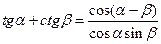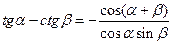
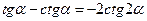
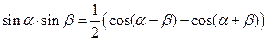
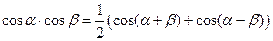
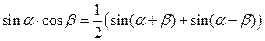
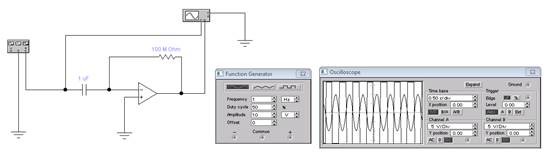
Вывод: на этой лабораторной работе я увидела, как работает интегратор, дифференциатор, отличия в их работе, изучила их схемы, параметры и характеристики. Узнала о том, как изменяется потенциал на выходе операционного усилителя в зависимости от знака на входе, определять напряжение сумматора с масштабными коэффициентом умножения.

ПОВТОРЕНИЕ НЕЗАВИСИМЫХ ОПЫТОВ. Несколько опытов называются независимыми, если вероятность исхода опыта не зависит от того, какие исходы имели другие опыты. Рассмотрим случай, когда вероятности исходов опытов постоянны и не зависят от номера опыта.

При проведении п независимых испытаний, в каждом из которых вероятность появления события равна р (0<р<1), вероятность наступления этого события ровно k раз описывается формулой Бернулли

.

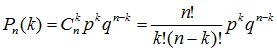т.е. в результате каждого опыта событие A появляется с вероятностью р и не появляется с вероятностью q=1-p.

Кроме того, вероятность наступления события не менее k1 раз и не более k2 раз (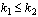) равна

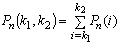
Следствия из формулы Бернулли.:

1.Вероятность того, что событие А наступит менее k раз

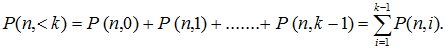(4.2)

2.Вероятность того, что событие наступит более k раз

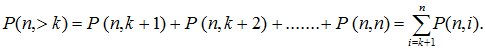(4.3)

3.Вероятность того, что в n опытах схемы Бернулли, событие А появится от k1 до k2 раз

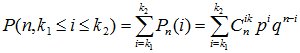. (4.4)

4.Вероятность того, что в n опытах событие А появится хотя бы один раз, определяется формулой

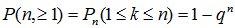(4.5)

Число к0, которому соответствует максимальная биномиальная вероятность 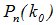, называется наивероятнейшим числом появления события А. При заданных n и p это число определяется неравенствами: 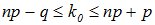. (4.6)

Схема Бернулли

Под схемой Бернулли понимают конечную серию 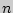повторных независимых испытаний с двумя исходами. Вероятность появления (удачи) одного исхода при одном испытании обозначают 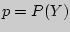, а непоявления (неудачи) его 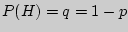. Я. Бернулли установил, что вероятность ровно 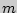успехов в серии из 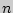повторных независимых испытаний вычисляется по следующей формуле:

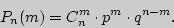
То значение 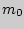, при котором число 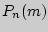является максимальным из множества { 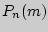}, называется наивероятнейшим, и оно удовлетворяет условию

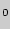
np - q m np+ p,

Формулу Бернулли можно обобщить на случай, когда при каждом испытании происходит одно и только одно из 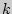событий с вероятностью 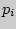(. Вероятность появления 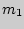раз первого события и 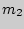- второго и 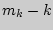-го находится по формуле

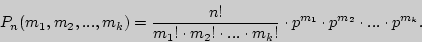
При достаточно большой серии испытаний формула Бернулли становится трудно применимой, и в этих случаях используют приближенные формулы. Одну из них можно получить из предельной теоремы Пуассона:

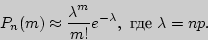
Таблица значений функции 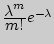имеется в приложении 3.

6.1. Спектр атома водорода. Правило отбора

6.2. Дуализм свойств микрочастиц. Соотношение неопределенностей Гейзенберга

6.3. Уравнения Шредингера (общие свойства)

6.4. Уравнение Шредингера (конкретные ситуации)

Дата добавления: 2015-06-04