Дифракция Фраунгофера. (дифракция в параллельных лучах)

(дифракция в параллельных лучах)

В случае сферических волн результат дифракции зависит от трех параметров: длины волны излучения, испускаемого источником S₀, геометрии препятствия (размеров щели, отверстия и т.д.) и расстояния от препятствия до экранов наблюдения. В условиях дифракции Фраунгофера осуществляется переход к плоским волнам, что исключает зависимость результата дифракции от третьей величины (расстояния от препятствия до экрана наблюдения), а геометрические размеры препятствия могут быть заранее учтены. В случае отверстия неизменных формы и размеров результат дифракции зависит только от изменения спектрального состава излучения, даваемого источником S₀. Поэтому дифракционные явления в параллельных лучах могут использоваться для спектрального анализа состава излучения исследуемых веществ.

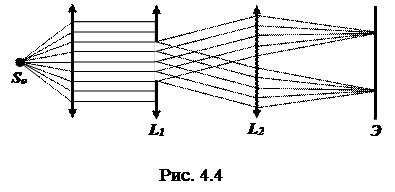
Принципиальная схема наблюдения плоских волн (дифракция Фраунгофера) изображена на рис. 4.4.

Свет от точечного источника S₀ превращается линзой L₁ в пучок параллельных лучей (плоскую волну), который проходит затем через отверстие в непрозрачном экране (круг, щель, и т.д.). Линза L₂ собирает в различных точках своей фокальной плоскости, где расположен экран наблюдения Э, все лучи, прошедшие через отверстие, в том числе и лучи, отклонившиеся от первоначального направления в результате дифракции.

Лучи, дифрагирующие под одним углом, линза L₂ собирает в одной точке фокальной плоскости Э.

Так как наблюдение дифракции по методу Фраунгофера ведется в том месте, где свет собирается линзой L ₂, то явление значительно выигрывает в яркости и наблюдение дифракционной картины облегчается.

Рассмотрим несколько случаев дифракции Фраунгофера.

Дифракция от одной щели. Практически щель представляется пря­мо­у­гольным отверстием, длина которого зна­чи­тельно больше ширины. В этом случае изо­бражение точки S₀ (рис. 4.4) рас­тя­нет­ся в полоску с минимумами и макси­му­ма­ми по направлению, перпендикулярному к ще­ли, ибо свет дифрагирует вправо и вле­во от щели (рис. 4.5). Если наблюдать изображение источника в направлении, пер­пендикулярном направлению образу­ю­щей щели, то можно ограничиться рас­смо­трением дифракционной картины в одном измерении (вдоль х).

Так как плоскость щели совпадает с фронтом падающей волны, то в соответствии с принципом Гюйген­са - Френеля точки щели являются вторичными источниками волн, колеб­лющихся в одной фазе.

Разобьем площадь щели на ряд узких полосок равной ширины, параллельных образующей щели. Фазы волн от разных полосок на одинаковых расстояниях равны, амплитуды также равны, ибо выбранные элементы имеют равные площади и одинаково наклонены к направлению наблюдения.

Если бы при прохождении света через щель соблюдался закон прямолинейного распространения света (не было бы дифракции), то на экране Э, установленном в фокальной плоскости линзы L₂, получалось бы изображение щели. Следовательно, направление j = 0 определяет недифрагированную волну с амплитудой A₀ , равной амплитуде волны, посылаемой всей щелью.

Из-за дифракции световые лучи отклоняются от прямолинейного направления на угол j. Отклонение вправо и влево симметрично относительно осевой линии OC₀ (рис. 4.5). Для отыскания действия всей щели в направлении, определяемом углом j, необходимо учесть разность фаз, характеризующую волны, доходящие до точки наблюдения C _j от различных полосок (зон Френеля).

Проведем плоскость FD, перпендикулярную к направлению дифрагированных лучей и представляющую фронт новой волны. Так как линза не вносит дополнительной разности хода лучей, ход всех лучей от плоскости FD до точки C _j одинаков. Следовательно, полная разность хода лучей от щели FE задается отрезком ED. Проведем плоскости, параллельные волновой поверхности FD, таким образом, чтобы они разделили отрезок ED на несколько участков, каждый из которых имеет длину l /2 (рис. 4.5). Эти плоскости разделят щель на вышеупомянутые полоски - зоны Френеля, причем разность хода от соседних зон равна l /2 в соответствии с методом Френеля. Тогда результат дифракции в точке C _j определится числом зон Френеля, укладывающихся в щели (см. дифракцию Френеля на круглом отверстии): если число зон четное (z = 2 k), в точке C _j наблюдается минимум дифракции, если z - нечетное (z = 2 k + 1), в точке C _j - максимум дифракции. Число зон Френеля, укладывающихся на щели FE, определяется тем, сколько раз в отрезке ED содержится l/ 2 т.е. 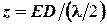. Отрезок ED, выраженный через ширину щели а и угол дифракции j, запишется как ED = а sin j.

В итоге для положения максимумов дифракции получаем условие

а sin j = ±(2 k + 1) l / 2,(4.7)

для минимумов дифракции

а sin j = ± 2 k l /2,(4.8)

где k = 1,2,3.. - целые числа. Величина k, принимающая значения чисел натурального ряда, называется порядком дифракционного максимума. Знаки ± в формулах (4.7) и (4.8) соответствуют лучам света, дифрагирующим от щели под углами + j и - j и собирающимся в побочных фокусах линзы L ₂: C _j и C_{- j}, симметричных относительно главного фокуса C₀. В направлении j = 0 наблюдается самый интенсивный центральный максимум нулевого порядка.

Положение максимумов дифракции по формуле (4.7) соответствует углам

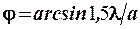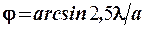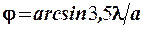, , и т.д.

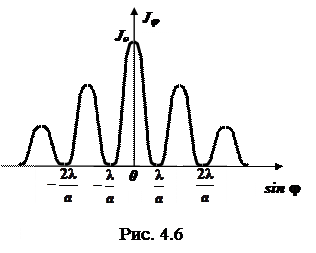
На рис. 4.6 приведена кри­вая распределения интен­сив­но­сти света в функции sin j. По­ло­жение цен­траль­ного макси­му­ма (j = 0) не за­висит от длины вол­ны и, сле­до­вательно, явля­ется общим для всех длин волн. Поэтому в слу­чае белого света центр диф­рак­ци­онной картины представится в виде белой по­лос­ки. Из рис. 4.6 и формул (4.7) и (4.8) ясно, что положение максимумов и ми­нимумов зави­сит от длины вол­ны. Поэтому простое че­ре­до­ва­ние темных и светлых полос имеет место только при монохроматическом свете. В случае белого света дифракционные картины для волн с разными l сдвигаются в соответствии с длиной волны. Центральный максимум белого цвета имеет радужную окраску только по краям (на ширине щели укладывается одна зона Френеля). Боковые максимумы для разных длин волн уже не совпадают между собой; ближе к центру располагаются максимумы, соответствующие более коротким волнам. Длинноволновые максимумы отстоят друг от друга дальше ( j = arcsin l /2), чем коротковолновые. Поэтому дифракционный максимум представляет собой спектр, обращенный к центру фиолетовой частью.

Дифракционная решетка

Дифракционная решетка представляет собой систему большого числа одинаковых по ширине и параллельных друг другу щелей, лежащих в одной плоскости и разделенных непрозрачными промежутками, равными по ширине. Дифракционная решетка изготавливается путем нанесения параллельных штрихов на поверхность стекла. Число штрихов на 1 мм определяется областью спектра исследуемого излучения и изменяется от 300 мм^-1 в инфракрасной области до 1200 мм^-1 в ультрафиолетовой.

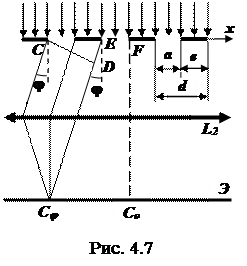
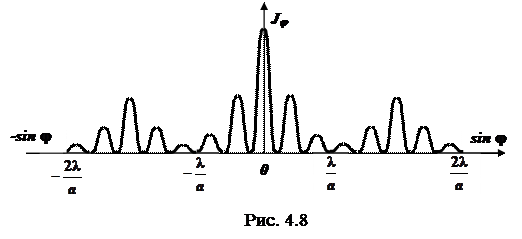
Пусть решетка состоит из N парал­лель­ных щелей с шириной каждой щели a и расстоянием между соседними ще­ля­ми b (рис. 4.7). Сумма a + b = d на­зы­­­ва­ет­ся периодом или постоянной ди­фра­к­ци­он­ной решетки. Пусть на решетку нор­мально па­дает плоская моно­хро­ма­ти­ческая вол­на. Требуется исследовать ин­тенсив­ность света, распро­стра­ня­ю­ще­­­гося в направле­нии, со­ста­вля­ю­щем угол j с нор­малью к плоскости ре­шетки. Кроме рас­пределе­ния ин­тен­сив­ности из-за ди­ф­ра­кции на каждой ще­ли, имеет мес­то перерас­пре­деление световой энер­гии за счет интерференции волн от N щелей когерентных источников. При этом минимумы будут находиться на прежних местах, ибо условие минимума дифракции для всех щелей (рис. 4.8) одинаково. Эти минимумы называются главными. Условие главных минимумов a sin j = ± k l совпадает с условием (4.8). Положение главных минимумов sin j = ± l /a, 2 l /a,... показано на рис. 4.8.

Однако в случае многих щелей к главным минимумам, создаваемым каждой щелью в отдельности, добавляются минимумы, возникающие в результате интерференции света, прошедшего через различные щели. На рис. 4.8 для примера показано распределение интенсивности и расположение максимумов и минимумов в случае двух щелей с периодом d и шириной щели a.

В одном и том же направлении все щели излучают энергию колебаний одинаковой амплитуды. И результат интерференции зависит от разности фаз колебаний, исходящих от сходственных точек соседних щелей (например, C и E, B и F), или от оптической разности хода ED от сходственных точек двух соседних щелей до точки C _j. Для всех сходственных точек эта разность хода одинакова. Если ED = ± k l или, так как ED = d si n j,

d sin j = ± k l, k = 0,1,2..., (4.9)

колебания соседних щелей взаимно усиливают друг друга, и в точке C _j фокальной плоскости линзы наблюдается максимум дифракции. Амплитуда суммарного колебания в этих точках экрана максимальна:

A_max = N A _j, (4.10)

где A _j - амплитуда колебания, посылаемого одной щелью под углом j. Интенсивность света

J_max = N²A _j ² = N²J _j. (4.11)

Поэтому формула (4.9) определяет положение главных максимумов интенсивности. Число k дает порядок главного максимума.

Положение главных максимумов (4.9) определяется соотношением

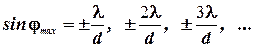. (4.12)

Максимум нулевого порядка один и расположен в точке C₀, максимумов первого, второго и т.д. порядков по два и расположены они симметрично относительно C₀, на что указывает знак +. На рис. 4.8 показано положение главных максимумов.

Кроме главных максимумов, имеется большое число более слабых побочных максимумов, разделенных добавочными минимумами. Побочные максимумы значительно слабее главных. Расчет показывает, что интенсивность побочных максимумов не превышает 1/23 интенсивности ближайшего главного максимума.

В главных максимумах амплитуда в N раз, а интенсивность в N ² раз больше амплитуды, даваемой в соответствующем месте одной щелью. Четко локализованные в пространстве линии с увеличенной яркостью легко обнаруживаются и могут быть использованы в целях спектроскопических исследований.

По мере удаления от центра экрана интенсивность дифракционных максимумов убывает (увеличивается расстояние от источников). Поэтому не удается наблюдать все возможные дифракционные максимумы. Заметим, что количество дифракционных максимумов, даваемых решеткой по одну сторону экрана, определяется условием ½ sin j½ £ 1 (j = p / 2 - максимальный угол дифракции), откуда с учетом (4.9)

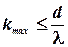. (4.13)

При этом не следует забывать, что k - целое число.

Положение главных максимумов зависит от длины волны l. Поэтому при освещении дифракционной решетки белым светом все максимумы, кроме центрального (k = 0), разложатся в спектр, обращенный фиолетовым концом к центру дифракционной картины. Таким образом, дифракционная решетка может служить для исследования спектрального состава света, т.е. для определения частот (или длин волн) и интенсивности всех его монохроматических компонент. Применяемые для этого приборы называются дифракционными спектрографами, если исследуемый спектр регистрируется с помощью фотопластинки, и дифракционными спектроскопами, если спектр наблюдается визуально.

Дата добавления: 2015-06-04