Свойства волн де Бройля

Рассмотрим движение свободного электрона. По де Бройлю, ему соответствует длина волны:

_.

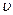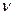Будем называть ее электронной волной. Известно, что λ = _фаз / , где 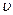_фаз – фазовая скорость распространения волны. Найдем фазовую скорость волны де Бройля:

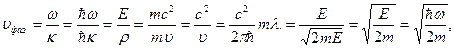
т. е. фазовая скорость зависит от частоты 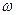, а значит дебройлевские волны об­ладают дисперсией даже в вакууме. В соответствии с современной физической интерпретацией фа­зовая скорость дебройлевских волн имеет чисто символиче­ское значение, поскольку эта интерпретация относит их к чис­лу принципиально ненаблюдаемых величин.

Т.к. c > 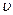, то фазовая скорость волн де Бройля больше скорости света в вакууме.

Найдем групповую скорость волны де Бройля:

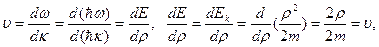
где 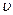– скорость частицы.

Установление того факта, что групповая ско­рость дебройлевских волн равна скорости частицы, сыграло в свое время важную роль в развитии принципиальных основ квантовой физики, и в первую очередь в физической интерпре­тации дебройлевских волн. Сначала была сделана попытка рас­сматривать частицы как волновые пакеты весьма малой протя­женности и таким образом решить парадокс двойственности свойств частиц. Однако подобная интерпретация оказалась оши­бочной, так как все составляющие пакет гармонические волны распространяются с разными фазовыми скоростями. При нали­чии большой дисперсии, свойственной дебройлевским волнам даже в вакууме, волновой пакет «расплывается». Для частиц с массой порядка массы электрона пакет расплывается практиче­ски мгновенно, в то время как частица является стабильным образованием.

Таким образом, представление частицы в виде волнового паке­та оказалось несостоятельным. Проблема двойственности свойств частиц требовала иного подхода к своему решению.

Прежде всего убедимся, что гипотеза де Бройля не противо­речит понятиям макроскопической физики. Возьмем в качест­ве макроскопического объекта, например, пылинку, считая, что ее масса т = 1 мг и скорость 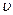= 1 мкм/с. Соответствующая ей дебройлевская длина волны

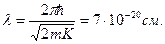
Т.е. даже у такого небольшого микроскопического объекта как пылинка дебройлевская длина волны оказывается неизмеримо меньше размеров самого объекта. В таких условиях никакие волновые свойства, конечно, проявить себя не могут.

Иначе обстоит дело, например, у электрона с кинетической энергией и импульсом 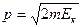. Его дебройлевская длина волны

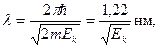
где в эВ. При = 150 эВ дебройлевская длина волны электро­на равна λ ~0,1 нм или ~1 . Такой же порядок величины имеет постоянная кристаллической решетки. Поэтому, аналогично тому, как в случае рентгеновских лучей, кристалли­ческая структура может быть подходящей решеткой для получе­ния дифракции дебройлевских волн электронов.

Сведем корпускулярные и волновые свойства свободных частиц в таблицу и покажем их связь:

Корпускулярные свойства Волновые свойства

Скорость 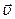, импульс 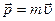Длина волны де Бройля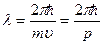

Энергия 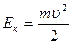Частота волны де Бройля ω =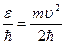

Групповая скорость волн де Бройля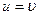

Фазовая скорость волн де Бройля

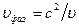
Волны де Бройля не электромагнитные. Распространение их не связано с распространением в пространстве какого-либо электромагнитного поля. Волны де Бройля, связанные с частицами вещества, имеют специфическую квантовую природу, не имеющую аналогов в классической физике. Вопрос о природе волн, связанных с частицами вещества, в квантовой механике рассматривают как вопрос о физическом смысле амплитуды этих волн. Вместо амплитуды рассматривают интенсивность волны, которая пропорциональна квадрату модуля амплитуды.

В опытах по дифракции электронов было доказано неодинаковое распределение пучков электронов, отраженных или рассеянных по различным направлениям. Выделялись направления, в которых рассеивалось большее число электронов. Наличие максимума числа электронов в некоторых направлениях означает, что эти направления соответствуют наибольшей интенсивности волн де Бройля, т.е. интенсивность волн в данной точке пространства определяет число электронов, попавших в эту точку за 1 секунду. Таким образом, квадрат модуля амплитуды волн де Бройля в данной точке является мерой вероятности того, что частица находится в этой точке.

Подтвержденная на опыте идея де Бройля о корпускулярно-волновом дуализме микрочастиц принципиально изменила представления об облике микромира. Поскольку всем микрообъектам (частицам) присущи и волновые и корпускулярные свойства, то любую из этих частиц нельзя считать ни частицей, ни волной в классическом понимании этих слов. Возникла потребность в такой теории, в которой волновые и корпускулярные свойства материи выступали бы не как исключающие, а как взаимно дополняющие друг друга. В основу такой теории – квантовой механики – и легла гипотеза де Бройля.

Дата добавления: 2015-06-04