
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Волновая функция
|
|
|
|
E).
УРАВНЕНИЕ ШРЕДИНГЕРА
ЗАДАНИЯ № 6-11
Ниже приведены несколько видов уравнения Шредингера для общего и частного случаев:
А) 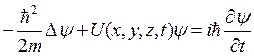 ;
;
Б) 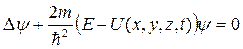 ;
;
В) 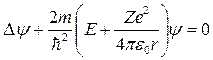 ;
;
Г) 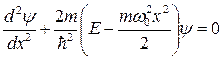 ;
;
Д) 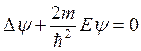 ;
;
ЗАДАНИЕ № 6
Общим уравнением Шредингера является…
ВАРИАНТЫ ОТВЕТОВ:
1) A; 2) Б; 3) В; 4) Г; 5) Д; 6) E.
ЗАДАНИЕ № 7
Уравнением Шредингера для стационарных состояний в общем случае является уравнение…
ВАРИАНТЫ ОТВЕТОВ:
1) A; 2) Б; 3) В; 4) Г; 5) Д; 6) E.
ЗАДАНИЕ № 8
Уравнением Шредингера для электрона в водородоподобном атоме является уравнение…
ВАРИАНТЫ ОТВЕТОВ:
1) A; 2) Б; 3) В; 4) Г; 5) Д; 6) E.
ЗАДАНИЕ № 9
Стационарным уравнением Шредингера для линейного гармонического осциллятора является уравнение…
ВАРИАНТЫ ОТВЕТОВ:
1) A; 2) Б; 3) В; 4) Г; 5) Д; 6) E.
ЗАДАНИЕ № 10
Уравнением Шредингера для частицы в трехмерной прямоугольной “потенциальной яме” с бесконечными прямоугольными стенками является уравнение…
ВАРИАНТЫ ОТВЕТОВ:
1) A; 2) Б; 3) В; 4) Г; 5) Д; 6) E.
ЗАДАНИЕ № 11
Уравнением Шредингера для частицы в одномерной прямоугольной “потенциальной яме” с бесконечными прямоугольными стенками является уравнение …
ВАРИАНТЫ ОТВЕТОВ:
1) A; 2) Б; 3) В; 4) Г; 5) Д; 6) E.
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
Указание к заданиям 6 -11.
Общее уравнение Шредингера:
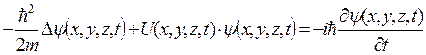 ,
,
где 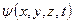 – волновая функция;
– волновая функция;
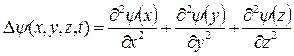 ;
;
m −масса частицы;
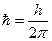 (
(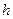 − постоянная Планка);
− постоянная Планка);
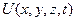 − потенциальная энергия.
− потенциальная энергия.
Для стационарного случая уравнение Шредингера:
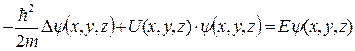 или
или
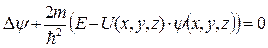 ,
,
где E – энергия частицы.
Для электрона в водородоподобном атоме функция потенциальной энергии 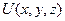 обладает центральной симметрией и задается выражением
обладает центральной симметрией и задается выражением 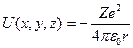 ,
,
где Z – число протонов в ядре (порядковый номер атома в таблице Менделеева);
Z e – заряд ядра (е – величина заряда электрона);
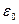 − электрическая постоянная;
− электрическая постоянная;
r – расстояние от ядра до точки (x, y, z).
Линейный гармонический осциллятор относится к одномерному случаю и потенциальная энергия задается выражением:
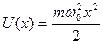 ,
,
где m − масса частицы;
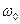 − собственная циклическая частота осциллятора;
− собственная циклическая частота осциллятора;
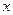 − координата частицы.
− координата частицы.
Для частиц в трехмерной или одномерной прямоугольной “потенциальной яме” с бесконечными прямоугольными стенками потенциальная энергия внутри “ямы” равна нулю (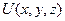 = 0 или
= 0 или 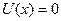 ).
).
ЗАДАНИЕ № 12
Если w − частота, h − постоянная Планка, то энергия основного состояния гармонического осциллятора равна:
1) 0;2) 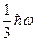 ; 3)
; 3) 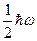 ; 4)
; 4) 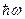 ; 5)
; 5) 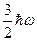 .
.
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
Указание к заданию 12
Для квантового гармонического осциллятора собственные значения энергии (энергетические уровни):
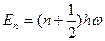 , где n = 0, 1, 2, …
, где n = 0, 1, 2, …
ЗАДАНИЕ № 13
На рисунках приведены картины распределения плотности вероятности нахождения электрона в потенциальном ящике с бесконечно высокими стенками.
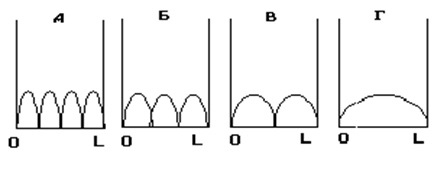
Какая из картин соответствует состоянию с квантовым числом n=3?
ВАРИАНТЫ ОТВЕТОВ:
1) А; 2) Б; 3) В; 4) Г; 5) Ни одна из них.
ЗАДАНИЕ № 14
На рисунке приведен график волновой функции электрона в “потенциальной яме”.
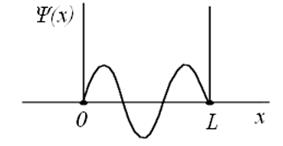
Вероятность нахождения электрона на отрезке 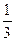 L < x <
L < x < 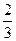 L равна...
L равна...
ВАРИАНТЫ ОТВЕТОВ:
1) 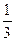 ; 2)
; 2) 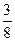 ; 3)
; 3) 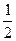 ; 4)
; 4) 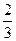 ; 5)
; 5) 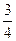 .
.
ЗАДАНИЕ № 15
Вероятность обнаружить электрон на участке (a,b) одномерного потенциального ящика с бесконечно высокими стенками вычисляется по формуле 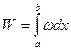 , где w − плотность вероятности, определяемая
, где w − плотность вероятности, определяемая 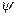 - функцией. Если
- функцией. Если 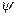 -функция имеет вид, указанный на рисунке, то вероятность обнаружить на участке
-функция имеет вид, указанный на рисунке, то вероятность обнаружить на участке 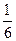 L < x <
L < x < 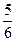 L равна:
L равна:


ВАРИАНТЫ ОТВЕТОВ:
А) 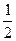 ; Б)
; Б) 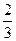 ; В)
; В) 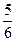 ; Г) 1.
; Г) 1.
ЗАДАНИЕ № 16
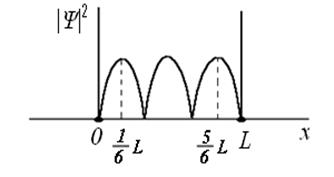
На рисунке приведена картина распределения плотности вероятности нахождения электрона в потенциальном ящике с бесконечно высокими стенками. Вероятность обнаружить электрон на отрезке 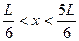 равна...
равна...
ВАРИАНТЫ ОТВЕТОВ:
1) 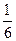 ; 2)
; 2) 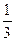 ; 3)
; 3) 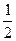 ; 4)
; 4) 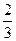 ; 5)
; 5) 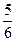 .
.
ЗАДАНИЕ № 17
Микрочастица с энергией Е > UO находится в потенциальном поле, вид которого изображен на рисунке.
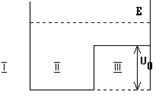
Каков вид волновой функции на участке II?
A) 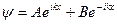 ;
; 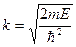 ;
;
Б) 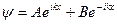 ;
; 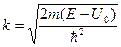 ;
;
В) 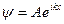 ;
; 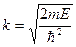 ;
;
Г) 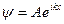 ;
; 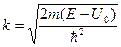 ;
;
Д) 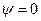 .
.
ВАРИАНТЫ ОТВЕТОВ:
1) А; 2) Б; 3) В; 4) Г; 5) Д.
ЗАДАНИЕ № 18
 Микрочастица с энергией Е > UO находится в потенциальном поле, вид которого изображен на рисунке.
Микрочастица с энергией Е > UO находится в потенциальном поле, вид которого изображен на рисунке.
Каков вид волновой функции на участке III?
A) 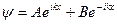 ;
; 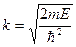 ;
;
Б) 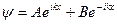 ;
; 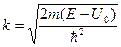 ;
;
В) 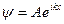 ;
; 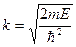 ;
;
Г) 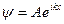 ;
; 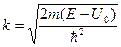 ;
;
Д) 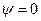 .
.
ВАРИАНТЫ ОТВЕТОВ:
1) А; 2) Б; 3) В; 4) Г; 5) Д.
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
Указание к заданиям 12 - 18.
Для частицы, находящейся в одномерной “потенциальной яме” с бесконечными стенками и плоским дном волновая функция Ψn(х) имеет следующий вид:
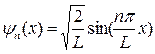 ,
,
где L – ширина “потенциальной ямы”,
n – главное квантовое число (номер квантового состояния), которое характеризует энергетический уровень. В этом случае плотность вероятности 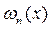 будет иметь вид:
будет иметь вид:
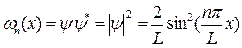 , где знак * означает комплексное сопряжение.
, где знак * означает комплексное сопряжение.
На участке 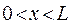 волновая функция Ψn(х) имеет n экстремумов, а функция плотности вероятности
волновая функция Ψn(х) имеет n экстремумов, а функция плотности вероятности 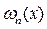 имеет n максимумов.
имеет n максимумов.
Вероятность 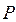 обнаружить электрон на участке (
обнаружить электрон на участке (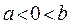 ) вычисляется по формуле:
) вычисляется по формуле:
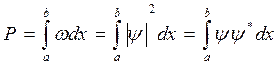 . (3)
. (3)
При этом вероятность 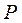 обнаружить электрон на всем участке L (
обнаружить электрон на всем участке L (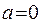 ,
, 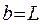 ) равна единице, т.е. с учетом геометрического смысла определенного интеграла площадь под кривой
) равна единице, т.е. с учетом геометрического смысла определенного интеграла площадь под кривой 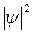 на всем участке L (
на всем участке L (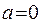 ,
, 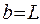 ) равна единице, а вероятность обнаружить электрон на интервале (
) равна единице, а вероятность обнаружить электрон на интервале (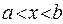 ) равна отношению площадей под кривой
) равна отношению площадей под кривой 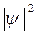 на этом интервале (
на этом интервале (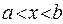 ) и на всем интервале (
) и на всем интервале (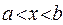 ) для
) для 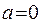 ,
, 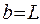 .
.
Для частицы, находящейся в одномерной “потенциальной яме” с бесконечными стенками и ступенчатым дном волновая функция 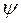 на участке с высотой ступеньки U0 имеет следующий вид:
на участке с высотой ступеньки U0 имеет следующий вид:
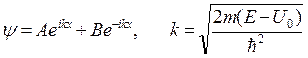 ,
,
где E – уровень энергии.
|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 2969; Нарушение авторских прав?; Мы поможем в написании вашей работы!