Обратное распространение ошибки

Одним из самых распространенных алгоритмов обучения нейросетей прямого распространения является алгоритм обратного распространения ошибки ( BackPropagation, BP). Этот алгоритм был переоткрыт и популяризован в 1986 г. Румельхартом и МакКлелландом из группы по изучению параллельных распределенных процессов в Массачусетском технологическом институте. Здесь я хочу подробно изложить математическую суть алгоритма, так как очень часто в литературе ссылаются на какой-то факт или теорему, но никто не приводит его доказательства или источника. Честно говоря, то же самое относится к Теореме об отображении нейросетью любой функциональной зависимости, на которой основываются все попытки применить нейросети к моделированию реальных процессов. Я бы хотел посмотреть на ее доказательство, но еще нигде его не смог найти. Вот, чтобы у Вас не возникало такого чувства неудовлетворенности в полноте понимания работы нейросети, я решил привести этот алгоритм полностью, хотя честно сознаюсь, что не совсем понимаю его логику.

Итак, это алгоритм градиентного спуска, минимизирующий суммарную квадратичную ошибку:

.

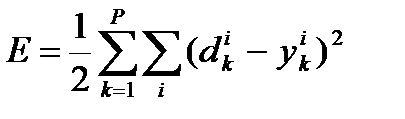Здесь индекс i пробегает все выходы многослойной сети.

Основная идея ВР состоит в том, чтобы вычислять чувствительность ошибки сети к изменениям весов. Для этого нужно вычислить частные производные от ошибки по весам. Пусть обучающее множество состоит из Р образцов, и входы k-го образца обозначены через {xⁱ _k}. Вычисление частных производных осуществляется по правилу цепи: вес входа i-го нейрона, идущего от j-го нейрона, пересчитывается по формуле:

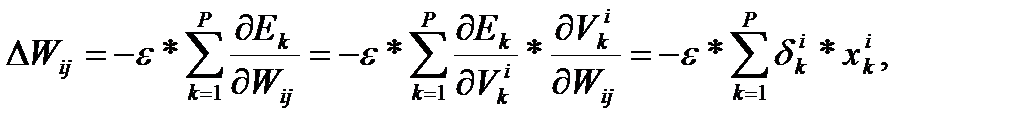
где e - длина шага в направлении, обратном к градиенту.

Если рассмотреть отдельно k-тый образец, то соответствующиее изменение весов равно:

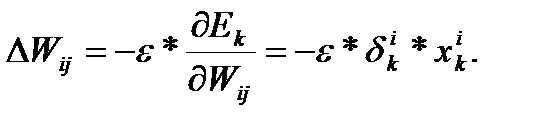
Множитель dⁱ_k вычисляется через аналогичные множители из последующего слоя, и ошибка, таким образом, передается в обратном направлении.

Для выходных элементов получим:

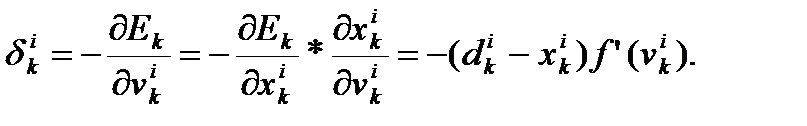
Для скрытых элементов множитель dⁱ_k определяется так:

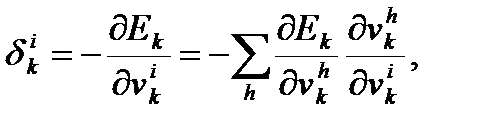
где индекс h пробегает номера всех нейронов, на которые воздействует i-ый нейрон.

Чтобы наглядно представить себе алгоритм обратного распространения ошибки, можно посмотреть следующий рисунок 7:

Рис. 7

Дата добавления: 2015-06-04