Годовое изменение параметров Земли 1 страница

2006 07 10 29.28025 1,547043 5,892235 6,584805

2005 06 24 29.28715 1,546472 5,893322 6,582375

2006 12 24 30.28670 1,445932 6,094769 6,154438

2006 01 01 30.29838 1,444818 6,097119 6,149696

2005 01 09 30.29602 1,445043 6,096644 6,150654

2005 01 10 30.29581 1,445063 6,096602 6,150738

2005 12 31 30.29818 1,444836 6,097079 6,149775

2006 01 02 30.29770 1,444882 6,096983 6,149969

2006 12 23 30.28661 1,445941 6,094752 6,154474

2006 12 25 30.28615 1,445985 6,094658 6,154663

Максимальную скорость планета имеет в тот же день, в который расстояние между ней и Солнцем минимально.

Таблица 21. На максимальном расстоянии:

v R M_з R_з

2005 06 23 29.287751 1,5462505 5,893744 6,581431

2005 06 25 29.287362 1,5462916 5,893665 6,581606

2006 07 09 29.280698 1,5469955 5,892326 6,584603

2006 07 11 29.280554 1,5470107 5,892297 6,584667

Минимальную скорость планета имеет в тот же день, в который расстояние между ней и Солнцем максимально. Т.е. никаких нарушений принципов классической механике не происходит.

Итак, диаграммы графиков 12 и 16 показывает изменение радиуса и скорости орбитального движения планеты в пульсирующем режиме. А раз так, то в соответствии с принципом инвариантности, в таком же режиме пропорционально радиусу и скорости должны изменяться количественные величины всех параметров Земли: масса М, радиус r, напряженность гравитационного поля g, гравитационная «постоянная» G, плотность ρ и т.д. А вместе с количественным изменением параметров Земли так же пропорционально им, меняется численная величина всех свойств тел, находящихся на ее поверхности. И это количественное изменение всех параметров, обусловленное изменением скорости орбитального движения планеты, явственно отображается только на изменении веса тел F, находящихся на ее поверхности. Именно это изменение веса тел на поверхности Земли и было обнаружено экспериментально. Однако остается вопрос: Какие причины скрывают истинную траекторию орбитального движения Земли? Попробуем разобраться в этом вопросе.

Прежде чем перейти к поэлементному расчету изменения параметров Земли отмечу еще раз, что в соответствии с принципом инвариантности, внешние и внутренние параметры планеты определяются ее положением на орбите. Последнее обусловливает одинаковую пропорциональную взаимосвязь внешних и внутренних свойств, что позволяет производить расчеты параметров одной системы по «комплексным» («смешанным») инвариантам. Под смешанными инвариантами понимаются уравнения, включающие как внешние параметры, например, скорость движения планеты по орбите, так и внутренние параметры, например, массу или радиус Земли. В качестве примера приведу инвариант с указанными параметрами:

М_з ∕v_з = Б, (4.11)

где: М_з – масса Земли, а v_з – ее орбитальная скорость.

Или другие инварианты:

R_n²g_n = R_nv_nз² = В, (4.12)

R_nМ_п² = Г, и т.д. (4.13)

где: R_n – орбитальный радиус в n- й день, g_n – напряжённость гравитационного поля Земли (ускорение свободного падения на поверхности планеты) в тот же день, v_nз – первая орбитальная скорость у поверхности Земли, Б, В, Г – инварианты.

В закон всемирного тяготения И. Ньютона входят m, М, R_з, G и F. В соответствии с принципом инвариантности все они должны изменяться при движении планеты вокруг светила. Диаграммы изменения скорости планеты и радиуса орбиты определены (графики 14 и 15). Теперь, опираясь на них, найдем по инвариантам (4.11)-(4.13) изменение параметров m, М, R_з, G и F. Начнем с расчета ежедневного изменения массы Земли.

Для корректного расчета изменения массы необходимо определиться с тем, на какой временной период приходится известная на сегодня величина массы равная М_з = 5,978∙10²⁷ г. Естественно предположить, что требуемую массу планета может иметь тогда, когда она находится в той области времени, в которой на графике 15 совпадают радиусы орбит, полученные по расчету инвариантов и по таблице эфемерид. И все известные параметры планеты М_з, R_з, G_з, g и т.д. следует отнести к одному из этих дней.

Вырежем фрагменты гр а фика 15 в окрестностях пересечения радиусов, полученных по таблице эфемерид – ряд 1 и по инварианту (4.4) – ряд 2, и посмотрим, на какие числа приходятся даты пересечения;

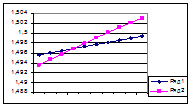На графиках 17 и 18 показаны фрагменты диаграммы годового изменения радиусов орбит исполненные по (4.3) и по таблице эфемерид. На этих фрагментах диаграммы пересекаются в двух точках: 30-го сентября 2005 г. и 6-го апреля 2006 г. Место пересечения показывает, что в эти дни расстояние

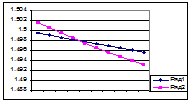
График17. График18.

от планеты до Солнца по эфемеридам лаборатории реактивного движения и по инвариантному расчету будут близки к совпадению. И, следовательно, все числовые параметры планеты для обеих диаграмм будут примерно одинаковыми. Примем массу Земли на 6 апреля равной М_з = 5,978∙10²⁷ г. и определим диаграмму её изменения за год.

Массу можно определить по нескольким инвариантам.

По изменению скорости на орбите:

М_n/v_n = const₁. (4.14)

По изменению расстояния до Солнца:

R_nM_n² = const. (4.15)

По неизменности момента количества движения µ:

R_nv_nM_n = µ = const. (4.16)

И т.д.

Результаты всех расчетов по этим инвариантам будут тождественны.

Предположим, что масса М_n рассчитывается по инварианту (4.11); тогда равенство расстояний приходится на 6 апреля 2006 г. и величина инварианта равна:

М_n/v_n = 2,0123583·10²¹ гсек/см. (4.17)

Преобразуя (4.11) относительно М_п имеем:

М_n = 2,0123583·10²¹· v_n,

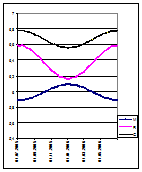и найдя, по изменению скорости движения, количественную величину массы Земли на каждый день года (приложение 2 столбец М_з), строим диаграмму изменения массы М_n (график 19).

Диаграмма М_n аналогична диаг-рамме изменения скорости движения планеты по орбите. Она свидетель-ствует о том, что масса Земли пуль-сирует с месячной и годовой частотой, изменяясь за полугодие в пределах: минимум ~ 5,893·10²⁷ г. на 24.06.2005 г., максимум 6,097110²⁷ г. на 01.01.2006 г.

График 19. Т.е. изменение величины массы наблюдается даже в первом знаке. Разница между максимумом и минимумом массы Землисоставляет ~2,049·10²⁶ г. Это почти в три раза больше принятой на сегодня массы Луны равной М_л = 7,35·10²⁵ г.

Аналогично рассчитываем изменение радиуса R_з планетыв течение года, используя различные инварианты. Например:

R_зМ_з² – const. (4.18)

Или,

R_зn v_n² – const₁, И т.д.

Для нахождения величины радиуса орбиты планеты на каждый день года используем инвариант (4.15):

R_зnМ_зn² = 2,279·10⁶⁴.

Полученные результаты занесем в приложение 2 диаграмма R_з и построим на графике 19 диаграмму R. Диаграмма R показывает, что радиус Земли уменьшается одновременно с возрастанием ее массы. Констатируем: согласно расчетам минимальный радиус R_з ≈ 6,1497 тыс. км. Земля имела 1 января 2006 г. Максимальным радиус Земли пришелся на 10 июля 2006 г. и составил R_з ≈ 6,5848 тыс. км. Амплитуда колебания радиуса ~ 435 км, Таким образом, теоретические параметры самопульсации Земли оказываются достаточно весомыми, и не могут не влиять на режим функционирования планеты и в первуюочередь погоды на ней.

Для расчета диаграммы изменения «постоянной» тяготения G_n можно также применить несколько инвариантов.

G_nv_n = const₂ (4.19)

G_n²∕R_n = const₃ = Д, И т.д. (4.20)

Для минимизации расчетов,употребим только один из них, например (4.20), причем радиусом в нем можно использовать как орбитальный радиус R_n, так и радиус Земли R_зn, естественно, что принимаются параметры по численной величине на 6 апреля 2006 г.:

G_n²∕R_зn = Д = (6,672·10^-6)²∕6,378·10⁸ = 6,97955·10^-20. (4.21)

Преобразовав (4.21) относительно G_n получаем:

G_n = √ ДR_n. (4.22)

И решив уравнение (4.22) на каждый день года, занесем полученные результаты в график 19, и получим диаграмму G изменения гравитационной «постоянной».

Таким образом, модули всех трех параметров М_n, R_зn,, и G_n оказываются синусоидально изменяемыми. Причем два из них, радиус и масса Земли изменяются в противофазе изменению гравитационной «постоянной».

Расчет силы «притяжения» можно производить по двум уравнениям:

по уравнению (а):

F_n = G_nm_nM_n/R_n² = Р_n,

и по уравнению (б):

F_n = m_ng_n.

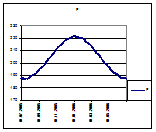
И то, и другое уравнение предполагает «неизменность» веса тела на некоторой поверхности во времени. И в том и в другом уравнении также присутствует «неиз-менная» масса некоего пробного тела. 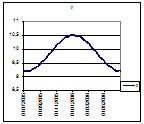В качестве пробного тела в данной работе используем свинцовый цилиндр весом на 6 апреля 2006 года 202,9 гр. Для получения силы притяжения F_n, например, по(б) необходимо знать изменение напряженности гравиполя График 20.планеты g_n и массы m_n на каждый день года. Напряжённость гравитационногополя (ускорение свободного падения) можно определить по инварианту:

R²g = А = 2,2014∙10²⁷ см³∕сек².

Рассчитаем изменение напряженности g и отобразим его на графике 20:

Напряженность гравитационного поля меняется за год от 9,22·10² см³⁄сек² до 10,55·10² см³⁄сек² в январе, т.е. на 1,33·10² см³⁄сек².

Осталось определиться с силой притяжения тела к Земле F и с его массой m. Силу притяжения также можно определять по нескольким инвариантам:

FR_з=Е (4.23)

F²R_з⁵= Ж и т.д.

Определимся, например, с количе- График 21. ственной величин инварианта (4.23):

FR_з²G = Е = 5,4916·10¹².

И, рассчитав параметр F_n на каждый день года, построим диаграмму графика 21. Диаграмма показывает, что вес свинцового цили-ндра изменяется с 187,33 грамма на 01.07.05 г. до 212,61 грамма на 01.01.06 г., т.е. на 25,28 гр.

Однако весы отображают величину практически на два порядка меньше. Это следствие одновременного уменьшения параметров всех тел под воздействием изменения гравиполя Земли (через массу эталонного тела).

Определим массу пробного тела исходя из параметров Земли на 6 апреля 2006 года:

m = Р⁄g = 0,20683 гр.,

и по инварианту (4.15):

v_n⁄m_n = 1,440874 = const₁,

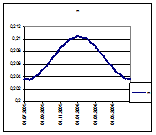определим количественную величину m_n на каждый день года с 01.07.05 до 01.07.06. Диаграмма графика 22 показывает, что изменение массы пробного тела за год аналогично изменению массы Земли ( график 19.) и силы при-тяжения Землей пробного тела (график 22.).Отмечу, что на графиках12-15отображены теоретические изменения параметров Земли, кото-рые при эмпирическом рассмотрении График 22. взаимодействия конкретных тел могут давать результаты, значительно отличающиеся от теоре-тических. Это обусловлено тем, что процесс измерения веса любого тела осуществляется опосредованно через некоторое промежуточное тело, илипружину,со свойствами, изменяющимися при изменении внешнего гравиполя.

4.4. Орбитальные пульсации Земли

Эту небольшую публикацию из сборника [66] с тем же названием, я привожу без изменения как при­мер орбитальной самопульсации Земли и Луны, совер­шенно не касаясь механики их движения в свете изло­женных выше электродинамических взаимодействий и с добавлением, тезисно, некоторых короткопериодических пульсаций земных сфер.

Траектории механического орбитального движения небесных тел Солнечной системы, в частности Земли и Луны, теоретически рассчитываются не по полевым уравнениям, как это делается, например, в электродина­мике, а достаточно искусственными методами возму­щающих движений. А потому правомерен вопрос: По­чему полевые методы теории гравитации практически не находят применения при расчете орбитального дви­жения планет?

Опуская рассмотрение методов возмущения как дос­таточно известных, попробую определить причины, обусловливающие отступление от полевых методов рас­чета орбит небесных тел на примере орбитального дви­жения планеты Земля.

Из классической механики известно, что планета Зем­ля движется по «инерции» на орбите в гравитационном поле Солнца со средней скоростью v_cp = 29,76 км/с, имея в перигелии скорость v_p = 30,27 км/с, а в афелии v_a = 29,27 км/с [57]. В 1995 г. по эфемеридам расстояние в перигелии от центра Солнца до Земли составляло R_p = 1,471·10¹³ см, а в афелии R_a = 1,521·10¹³ см, при среднем расстоянии R_cp = 1,49610¹³ см [108].

Воспользовавшись этими данными, определяем рас­четную напряженность гравиполя g на расстоянии, со­ответствующем этим точкам по формуле:

g_n = v_n²/R_n. (4.24)

И получаем, что в перигелии напряженность g_p = 0,62391 см/с², в афелии g_a = 0,56328 см/с², a g_cp = 0,59202 см/с².

Зная напряженность (ускорение свободного падения) гравиполя Солнца g_c = 2.738·10⁴ см/с², его радиус R_c = 6,96·10¹⁰ см и закон убывания напряженности — инва­риант (4.25):

R_с²g_c = 1,3263·10²⁶ - const, (4.25)

определяем для тех же областей пространства теорети­ческую напряженность гравитационного поля, созда­ваемую Солнцем. Она равна в перигелии g_p1 = 0,61296 см/с², в афелии g_a1 = 0,57332 см/с² и только в начале ап­реля и в октябре в моменты пересечения с расчетной, оказывается близкой к ней. Различие расчетных и теоре­тических параметров напряженности гравитационного поля уже во втором знаке (и, в частности, у Луны тоже) становится основной причиной затруднений при ис­пользовании полевых методов в расчете орбитального движения небесных тел. На диаграмме 1 графика 23 сплошной ли­нией 1отображено ежедневное расчетное изменение на­пряженности гравиполя в 1995 г., построенное по траек­тории движения Земли. Линия 2показывает реальную напряженность гравиполя на том же расстоянии от Солнца, на

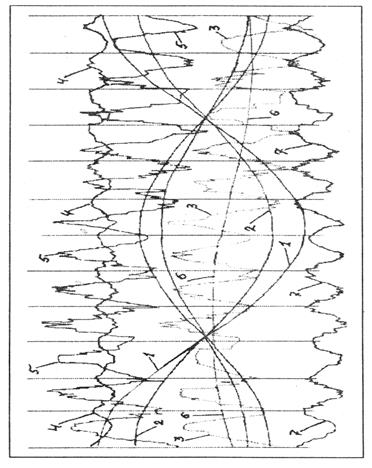
График 23

котором планета находится в соответствую­щий день. И, как явствует из диаграммы, наибольшая расчетная напряженность наблюдается в перигелии. За­тем, по мере увеличения расстояния от Солнца до Зем­ли, она, практически монотонно, убывает, сравниваясь с теоретической в начале апреля, и, продолжая убывать, достигает афелия в начале июля. В точке афелия проис­ходит перелом, и расчетная напряженность начинает возрастать, достигая средней величины в начале октября и максимума — в новом перигелии.

Фигура, образуемая этими двумя сходящимися ли­ниями, несколько напоминает полураскрытые ножницы. Угол между линиями 1 и 2 является основным препятст­вием применения полевых гравитационных уравнений. Никакого объяснения расхождению расчетной и теоре­тической напряженности мне обнаружить не удалось. И, по-видимому, современная небесная механика пренеб­регает этими ножницами, ограничиваясь при расчете траектории движения небесных тел уже упомянутым методом возмущений. К тому же классическая механика оставляет неизменными все параметры планет на про­тяжении всего их движения по орбите. А это может ока­заться одним из факторов, сдерживающих сближение теоретической и расчетной напряженностей.

Попробую, основываясь на принципах русской меха­ники, рассмотреть отдельные аспекты возможного из­менения параметров Земли при орбитальном движении.

Прежде всего, русская механика предполагает зависи­мость всех параметров движущегося тела от скорости его движения. И надо ожидать, что с возрастанием ско­рости v при движении планеты к перигелию или с ее уменьшением будет наблюдаться изменение радиуса R, гравитационной «постоянной» G, массы т, напряженно­сти гравитационного поля g и т.д. Поэтому, рассматри­вая на диаграмме 1 фактическую напряженность грави­тационного поля (линия 7) и зная, что она образуется радиусом и скоростью (4.24), необходимо определить форму связи этих внешних параметров с параметрами Земли. Например, с массой или гравитационной «посто­янной». И хотя бы предварительно определиться, будут ли они изменяться при движении планеты и каким образом.

Однако на любые изменения массы в классической механике, как уже говорилось, до сего дня наложено аб­солютное табу. Она постулируется неизменной всегда. Допускаются ее изменения только при скоростях, близ­ких к скорости света, которая, как известно, несопоставима с орбитальными скоростями, а потому при орби­тальных скоростях масса планеты меняться не может.

На изменение гравитационной «постоянной» G нало­жено табу помягче. Ее изменения допускаются. Более того, его ищут экспериментально и постоянно находят, но объяснение этому изменению в классической меха­нике еще нет.

В русской механике неизменные свойства отсутству­ют. Все свойства тел, в том числе и масса, и гравитаци­онная «постоянная» с изменением внешних условий ме­няют свою количественную величину. И потому, рассматривая медленное, почти монотонное ежедневное изменение линии 7 диаграммы 1, можно предположить, что и скорость на орбите, и расстояние от Солнца до планеты, и длина радиуса, и ее масса изменяются моно­тонно, а какая-то их совокупность остается неизменной и описывает соответствующую кривую. Задача заключа­ется в том, чтобы выделить из этой совокупности часть изменения, относящегося, например, к массе.

Классическая механика, как и русская, содержит урав-­
нение, которое включает в себя и массу т, и скорость v,
и радиус l. Это уравнение количества движения М:

M = mvl - const. (4.26)

И по законам классической механики, и по законам
русской механики (добавлю и по законам электродинамики, и квантовой механики) момент количества движе-ния, при свободном вращении или движении по орбите, всегда остается неизменным. То есть в приложении кдвижению планеты по орбите момент М по закону не может изменяться. Поскольку и в правой и в левой части
уравнения (4.26) имеются как бы неизменные величины
М и т, то его можно привести к виду:

М/т = vl - const. (4.27)

И оно будет таким при инерционном движении плане­ты по окружности, но не по эллипсу. При движении по эллипсу, как явствует из диаграммы 1 графика 23, произведение vl ≠ const, а значит и М/т ≠ const. И остается предполо­жить, что в движении по орбите меняется либо момент М, либо масса т. Поскольку момент «охраняется» зако­ном, в обеих механиках, а масса алогичным постулатом и только в одной, логично будет рассмотреть, изменяется ли масса планеты и по какому закону при ее движе­нии по орбите.

Можно, конечно, предположить, что в уравнении (4.26) меняется момент, а масса остается неизменной, или масса и момент изменяются в некоторой пропорции. Но из данных предположений следует, что изменения эти могут происходить только при некоторой форме взаимодействия движущейся планеты с окружающим пространством. Что конечно правильно и соответствует русской механике, но совершенно неприемлемо для ме­ханики классической.

В качестве точки отсчета для нахождения М было взя­то 4 апреля 1995 г., время, когда расчетная и теоретиче­ская напряженности сравниваются и, следовательно, скорость v = 2,9763·10⁶ см/с, массу т = 5,978·10²⁷ г и расстояние l = 1,4966·10¹³ см можно было принять за первичные исходные величины. В результате постоян­ная величина момента количества движения Земли по орбите оказалась равной М = 2,6628·10⁴⁷ г.см/с. (Еже­дневное расстояние до Солнца на 12 часов находим по эфемеридам [108], среднесуточную скорость определяем по [109]).

Зная величину количества движения М, преобразовы­ваем уравнение (6.19) относительно массы т:

m = M/Rv. (4.28)

Подставляя последовательно с 1 января 1995 г. в фор­мулу (4.28) ежедневную скорость и расстояние от цен­тра Солнца до центра Земли, определяем изменение ко­личественной величины массы на каждый день года и строим на графике 23 диаграмму 3. Она показывает, что масса планеты Земля, даже при относительно незначительном изменении скорости ее движения, систематически меняется в третьем-пятом знаке в пульсирующем режиме. Амплитуда колебания массы от максимума до минимума длится

около месяца, и масса изменяется от 5,972·10²⁷ г до 5,982·10²⁷ г. Изме­нение в третьем знаке происходит около раза в ме­сяц, четвертый и особенно пятый знак меняются почти ежедневно. Период одного колебания составляет около месяца и неравномерен по длительности. И в году укладывается 12 полных периодов (по результатам расчета 1994 — 1995 гг.).

Колебания переходят на следующий год таким образом, что помесячные максимумы преды­дущего года становятся минимумами последующего. Вместе с массой пропорционально пульсируют все ос­тальные параметры Земли, включая и гравитационную «постоянную» (линия 4). Именно это и фиксируется в работе [56]. Кроме того, просматривается общая для планеты волна с периодом около 12 месяцев, по-видимому, годовая (линия 6).

Пульсирующее изменение массы планеты сопровож­дается ежемесячным замедлением и ускорением ее дви­жения по орбите. И хотя относительное убывание и воз­растание скорости орбитального движения наблюдается почти на протяжении всего года, абсолютная, угловая скорость w на протяжении месяца то возрастает, то за­медляется, что и свидетельствует о пульсации планеты

Как было показано ранее, масса Земли может изме­няться только пропорционально гравитационной «по­стоянной» G по инварианту:

MG = 3,998...·10²⁰, (4.29)

где G = 6,672·10^-8 - гравитационная «постоянная».

Формула (4.29) обусловливает возможность ежеднев­ного нахождения параметра G. И по форме, и по величине гравитационная «постоянная» будет изменяться как обратное подобие изменения массы, что и наблюда­ется на диаграмме (линия 4). Следует еще раз отме­тить, что систематическое изменение G в третьем и чет­вертом знаках на протяжении полутора десятилетий фиксируется приборами [56]. Естественно, что приборы будут фиксировать не ту величину изменения гравита­ционной постоянной, которая отображена линией 4,а примерно такую, которую изображает линия 5. Аналогичным образом можно по инварианту:

M²R = 3,5736 10⁵⁶ - const₁, (4.30)

определить амплитуду колебания радиуса Земли (диаг­рамма 5). И оказывается, что месячные измене­ния радиуса достигают почти 20 км (тот же третий знак) оставаясь для нас и наших приборов почти незаметны­ми. Как тут не вспомнить А. Пуанкаре [17]: «если бы все тела Вселенной начали одновременно и в одинаковой пропорции расширяться (или, например, пульсируя, сжиматься и расширяться — А. Ч.), то у нас не было бы никаких средств заметить это, потому что все наши измерительные инструменты увеличивались бы одно­временно с самими предметами, для измерения которых они служат. После этого расширения мир продолжал бы свой ход и ничто не говорило бы нам, что произошло столь важное событие». (Курсив мой — А. Ч.)

И хотя это утверждение Пуанкаре достаточно катего­рично, в первом линейном приближении его можно счи­тать верным и подтверждаемым почти полным отсутст­вием приборной информации о пульсации Земли.

Надо отметить, что кроме двух вышеназванных пе­риодов (годового и месячного) существует хорошо из­вестный еще с древности 84,4-минутный период пуль­сации Земли — период Шулера [110], который накладывается на предыдущие и, по-видимому, имеет амплитуду колебания в пределах 1,5 км (на графике 23 он не отображен).

Можно показать, основываясь на уравнении (4.28), что и Луна в процессе своего орбитального движения от пе­ригея до перигея за полный оборот вокруг Земли совер­шает один-два цикла пульсации. Не останавливаясь на анализе представленной диа­граммы, отмечу, что полученные результаты только каче­ственно свидетельствуют о наличии пульсации у небес­ных тел — планет и их спутников. Уточненные коли­чественные величины параметров пульсации могут быть получены только тогда, когда будут сведены к одной линии гравитационные ножницы — теоретическая и расчетная напряженности гравитационных полей в об­ласти орбитального движения Земли и Луны. Их нали­чие, по-видимому, более чем на порядок искажает кар­тину пульсации Луны и в несколько меньшей степени — Земли. И именно их наличие свидетельствует о недоста­точности нашего понимания сути гравитационных взаи­модействий.

Отмечу, что орбитальную пульсацию Земли и Луны, ускорение и торможение их в процессе движения, вызы­ваемые пульсацией, можно фиксировать многими физи­ческими, астрономическими и оптическими методами, различными гироскопическими, маятниковыми и грави­тационными приборами на поверхности Земли. В част­ности, из механических приборов наиболее чувстви­тельными к самопульсации Земли являются гироскопи­ческие прецессирующие приборы типа гироскопа Фесселя.

Выявление орбитальной пульсации небесных тел по­зволяет сделать следующие предварительные выводы:

• следует ожидать, что самопульсация Земли, как и других небесных тел, вызывает попеременное, с годовым, месяч­ным периодами и периодом Шулера, замедление и уско­рение своего движения по орбите.

М = тv²/w;

• ускорение и замедление Земли на периоде в год (го­довой период пульсации) - известны, и показаны ранее;

• экспериментальное доказательство регулярного ус­корения и торможения Земли с годовым, месячным и полуторача­совым периодом при движении по орбите будет очередным доказательством отсутствия в природе движения по инерции.

Кроме орбитальной пульсации с периодом от месяца и более у Земли и ее сфер наблюдаются короткопериодические пульсации от нескольких часов до десятков ми­нут и более продолжительные, охватывающие геологи­ческие эпохи в миллионы и миллиарды лет. Изучая эти временные периоды В.А. Марков в работе [69] делает вывод о том, что «любой конечный интервал времени представляет собой циклически организованный про­цесс, складывающийся из двух зеркально отраженных в пространстве времени модельно подобных полуциклов Т₁ и Т₂ с постоянным отношением длительности T₁/T₂ = 2/3».

Этот очень важный вывод он подтверждает как при­мерами из геологической шкалы времени, так и пульсационными процессами малой временной продолжитель­ности. Пропуская рассмотрение периодов и эпох гео­логического времени, остановлюсь на короткопериодических пульсациях и в первую очередь на периоде Шулера t_i = 84,4 мин. [110]: «Применительно к t_i дели­мость в отношении 2/3 отражает пульсацию t₁' и t₁'' ос­новного тона или моды, отличающуюся от других соб­ственных колебаний наибольшей амплитудой. Ожи­даемые их значения t_i' = 0,6, или t_i' = 50,8 мин., и t_i" = 0,4 или t_i" = 33.8 мин» — пишет В. Марков [69].

Дата добавления: 2015-06-04