Математико-картографическое моделирование

Аппроксимации – замена сложных или неизвестных функций другими, более простыми, свойства которых известны. Любую сложную поверхность можно приближенно представить в виде: z=f(x,y)+ε, где f(x,y)-некая аппроксимирующая функция, ε-остаток, не поддающийся аппроксимации. Функцию можно далее разложить в ряд. После чего с аппроксимируемой карты снимают ряд значений z 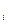и составляют систему уравнений, решаемых по МНК. (Необходимо, чтобы аппроксимирующее уравнение наилучшим образом описывало исходную поверхность, а сумма квадратов отклонений 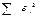= min).

Тригонометрические функции позволяют описывать сложные, сильно расчлененные поверхности, а сферические функции применяют, если нельзя пренебречь кривизной земли.

Приемы математической статистики – предназначены для изучения по картам пространственных и временных статистических совокупностей и образуемых ими статистических поверхностей. В основу всякого статистического исследования кладется выборка, т.е. некоторое подмножество однородных величин, снятых с карты по регулярной сетке точек (систематическая выборка), в случайно расположенных точках (случайная выборка), на ключевых участках (ключевая выборка) или по районам (районированная выборка). Выборочные данные группируют по интервалам, составляют гистограммы распределения и затем вычисляют различные статистики – количественные показатели, характеризующие пространственное распределение изучаемого явления. (ср. арифметич-ое, ср. квадр-ое, дисперсия, вариация и др.)

Другая задача-оценка взаимосвязи между явлениями – решается с помощью теории корреляции. Для этого необходимо иметь выборки по сравниваемым явлениям, показанным на картах разной тематики. Значения берутся в одних и тех же точках, а затем строят график поля корреляции.(Например карта испарения и карта температуры).

Приемы теории информации. Основная функция теории инф-ии- энтропия. Эта функция удобна для оценки степени однородности/неоднородности картографического изображения. Энтропией некоторой системы называется сумма произведений вероятностей различных состояний этой системы на логарифмы вероятностей, взятая с обратным знаком. (Если ф-ия=0, то изображение однородно (один контур), и ф-ия возрастает с увеличением числа контуров).

Дата добавления: 2015-06-04