ВВЕДЕНИЕ. Семестрова контрольна робота

Семестрова контрольна робота.

Дифракцией называют физические явления, наблюдаемые при распространении волн в среде с резкими неоднородностями, например огибание световыми волнами малых препятствий или проникновение света в область геометрической тени после прохождения узкого отверстия. Отклонения от законов геометрической оптики оказываются тем больше, чем меньше отношение размера отверстия или препятствия к длине световой волны.

Следует отметить, что между двумя характерными волновыми явлениями – дифракцией и интерференцией – нет существенного физического различия. Оба явления в случае световых волн заключаются в перераспределении светового потока в результате сложения волн. Только по историческим причинам перераспределение интенсивности, возникающее в результате сложения волн, возбуждаемых конечным числом дискретных источников, принято называть интерференцией волн. А перераспределение интенсивности, возникающее вследствие сложения волн, возбуждаемых когерентными источниками, расположенными непрерывно, принято называть дифракцией волн. Поэтому говорят, например, об интерференционной картине от двух узких щелей и о дифракционной картине от одной щели.

Различают два вида дифракции. Если лучи, падающие на препятствие или отверстие, образуют практически параллельные пучки, говорят о дифракции в параллельных лучах или дифракции Фраунгофера. В ином случае – о дифракции Френеля.

Впервые последовательно объяснить дифракцию света и дать методы ее количественного расчета удалось в начале XIX века французскому физику О. Френелю. При рассмотрении дифракции света Френель исходил из нескольких основных утверждений, принимаемых без доказательства и составляющих так называемый принцип Гюйгенса-Френеля. Проникновение световых волн в область геометрической тени может быть объяснено с помощью принципа Гюйгенса, согласно которому каждая точка волновой поверхности является источником вторичных волн. Однако принцип не дает сведений об амплитуде волн, распространяющихся в различных направлениях. Френель дополнил принцип Гюйгенса следующим предложением: 1) источники вторичных волн когерентны между собой, и результирующая волна в любой точке пространства является результатом интерференции вторичных волн; 2) мощности вторичного излучения равных по площади участков волновой поверхности одинаковы, и каждый вторичный источник излучает свет преимущественно в направлении внешней нормали к волновой поверхности.

Учет амплитуд и фаз вторичных волн позволяет найти амплитуду результирующей волны в любой точке пространства. Однако вычисление амплитуды световой волны согласно принципу Гюйгенса-Френеля представляет собой зачастую довольно сложную математическую задачу, и поэтому Френелем был предложен оригинальный метод разбивания волновой поверхности на зоны, позволяющий сильно упростить вычисление амплитуды. В этом методе волновая поверхность разбивается на площадки (зоны), расположенные так, что расстояние от краев каждой зоны до точки, в которой вычисляется амплитуда колебаний, отличается на половину длины волны.

Рассмотрим применение метода зон Френеля для исследования распределения интенсивности света после прохождения узкой щели. Пусть параллельный пучок монохроматического света падает нормально на узкую щель шириной b (рис. 1) и длиной а >> b. В соответствии с принципом Гюйгенса-Френеля каждая точка щели является источником вторичных волн, колеблющихся в одной фазе, так как плоскость щели совпадает с фронтом волны. За щелью лучи света распространяются под разными углами. На рис. 1 изображены лучи, дифрагирующие на угол φ после прохождения щели. Обычно для исследования картины распределения интенсивности за щелью помещается собирающая линза и экран в фокальной плоскости этой линзы. Тогда лучи, выходящие из щели под одинаковым углом, будут собираться линзой в одной точке на экране, и в результате интерференции таких лучей будет наблюдаться темное или светлое пятно.

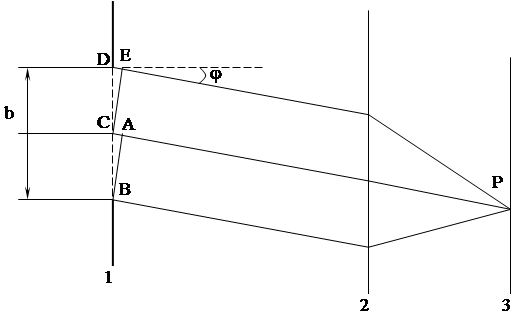Разобьем щель на зоны Френеля, имеющие вид полосок, параллельных ребру щели. По определению зоны Френеля лучи, идущие от краев каждой зоны, должны иметь разность хода, равную половине длины волны .

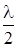Рис. 1. Схема хода лучей при дифракции параллельного пучка света (дифракции Фраунгофера) на узкой щели: 1 – непрозрачный экран с щелью; 2 – линза; 3 – экран для наблюдения распределения интенсивности света

Лучи, идущие от границ первой зоны Френеля из точек В и С, имеют разность хода .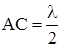

При интерференции света от каждой пары соседних зон амплитуда результирующего колебания в точке Р равна нулю, т. к. эти зоны вызывают колебания с одинаковыми амплитудами, но по фазе отличаются на π.

Если число зон, укладывающихся на щели, четное, то колебания каждой пары соседних зон гасят друг друга и результирующая амплитуда колебаний в точке Р будет равна нулю.

Если на ширине щели укладывается нечетное число зон Френеля, то колебания от всех зон, кроме одной, будут полностью скомпенсированы. Амплитуда колебаний в точке Р будет определяться только одной зоной Френеля.

Следует отметить, что ширина зоны Френеля зависит от угла дифракции φ. Из хода лучей на рис. 1 видно, что ширина одной зоны равна 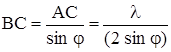. (Число зон равно отношению 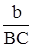, где b – ширина щели). Для четного числа зон выполняется условие

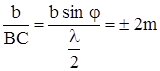, где m = 1, 2, 3 …;

или

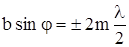. (1)

В этом случае на экране в точке Р будет наблюдаться темное пятно. Целое число m называется порядком дифракционного минимума.

Для нечетного числа зон, укладывающихся на щели, 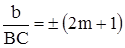, где m = 0, 1, 2, 3…, или

. (2)

В этом случае на экране в точке Р наблюдается светлое пятно.

Отдельно следует рассмотреть лучи, идущие от щели под углом φ = 0. Такие лучи собираются линзой в центре экрана, и колебания, вызываемые в точке Р всеми участками щели, будут совершаться в одной фазе. Следовательно, в этом направлении будет наблюдаться самый интенсивный максимум. Этот центральный максимум называется максимум нулевого порядка. Ему соответствует около 90 % всего светового потока, выходящего из щели.

Итак, используя метод зон Френеля, удалось довольно простым способом найти положение светлых и темных полос на экране при дифракции на узкой щели. Для более точного и детального выяснения картины распределения интенсивности света при дифракции на щели необходимо использовать принцип Гюйгенса-Френеля. Решение этой задачи можно провести следующим образом: щель разбивается на бесконечное число одинаковых, бесконечно узких полос, параллельных ребру щели. Вторичные волны, излучаемые такими полосками, будут цилиндрическими волнами с одинаковыми амплитудами. Суммирование этих волн сведется к интегрированию по всей ширине щели, и полученное выражение имеет вид

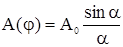, (3)

где А(j) – амплитуда колебаний в световой волне для точки на экране, в которой фокусируются лучи, идущие под углом j; А₀ – амплитуда колебаний в световой волне в центре экрана:

. (4)

Интенсивность света J(j) в различных точках экрана пропорциональна квадрату амплитуды А(j). Следовательно, используя уравнение (3), можем записать

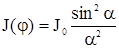, (5)

где J₀ – интенсивность света в центре экрана.

График зависимости интенсивности света на экране J(j) показан на рис. 2. По горизонтальной оси отложена величина a, пропорциональная углу дифракции j. При практических наблюдениях дифракции угол j обычно мал, и с хорошей точностью можно использовать соотношение .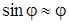

Тогда величина a с точностью до постоянного равна углу j.

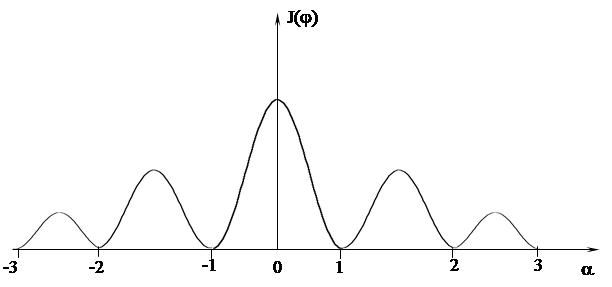
Рис. 2. График распределения интенсивности света на экране: по вертикальной оси – интенсивность света;

по горизонтальной – величина .

Используя формулы (2) и (5), можно найти относительные интенсивности максимумов

, (6)

где m – порядок максимума.

Численный расчет по формуле (6) показывает, что основная часть света приходится на центральный максимум. Ему соответствует около 90 % всего светового потока, выходящего из щели.

Количество максимумов на экране и их ширина зависят от ширины щели и расстояния до экрана. При уменьшении ширины щели центральный максимум будет становиться шире, а количество боковых максимумов становится меньше. Если, например, ширина щели равна длине волны, b = λ, то sin φ = 1, следовательно, φ = π/2, т. е. ни одного дифракционного минимума наблюдаться не будет, экран будет весь освещен: больше к середине и меньше к краям. Это соответствует чистой дифракции без интерференции. Если же случай противоположный, т. е. ширина щели во много раз больше длины волны, то чередование боковых максимумов будет очень частым и при большей ширине щели картина чередования светлых и темных полос практически не различна. Для ширины центрального максимума в этом случае из соотношения (1) можно получить ту же величину, как в геометрической оптике.

Присутствие линзы для наблюдения темных и светлых полос на экране необходимо при сравнительно небольшом расстоянии от щели до экрана. В случае когда ширина щели очень мала по сравнению с расстоянием до экрана, лучи от краев в точку Р будут практически параллельны и в отсутствии линзы между щелью и экраном.

Дата добавления: 2015-06-04