Увеличение галилеевой зрительной трубы

Если заменить положительный окуляр астрономической трубы отрицательным, получается галилеева (или земная) труба. При телескопическом ходе лучей в галилеевой трубе расстояние между объективом и окуляром равно разности (точнее алгебраической сумме) их фокусных расстояний (рис. 4.4), а изображение оправы объектива, даваемое окуляром, оказывается мнимым. Это изображение располагается между окуляром и объективом. Легко показать, что формула (4.4), выведенная для астрономической трубы, справедлива и для земной трубы.

Достоинством галилеевой трубы является то, что она дает прямое изображение. Поэтому зрительные трубы, бинокли и т.д. делаются по схеме Галилея.

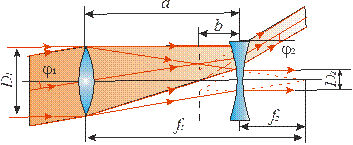
Рис. 4.4. Оптическая схема к расчету увеличения галилеевой

зрительной трубы

Пусть l₀ – предмет, отстоящий на расстояние d₀ от глаза наблюдателя (точки О), l – изображение предмета, видимое в трубу и находящееся на расстоянии d от точки О; a₀ и a – соответствующие углы зрения. Согласно определению увеличение

.

Спроецируем изображение l на плоскость предмета при помощи центральной проекции с центром в точке О, т.е. так, чтобы все точки изображения переместились вдоль лучей, соединяющих их с глазом наблюдателя. Спроецированное таким образом изображение займет положение L. Очевидно, что угол зрения, под которым видна эта проекция, – a, а расстояние ее от глаза есть d₀. В этом случае увеличение

.

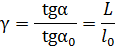Пусть предмет представляет собой шкалу, длина одного деления которого есть l₀. Если теперь выбрать такой отрезок шкалы, чтобы на нем улеглось n делений предмета и N делений изображения, где n и N числа целые и n>N, то можно записать, что nl₀=NL и, следовательно, увеличение трубы равно

.

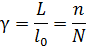Если предмет расположен не так, как указано на рис. 4.5, а пересекает ось прибора, то выражение не изменится. В этом можно легко убедиться, сделав соответствующее построение.

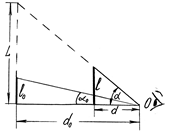
Рис. 4.5. Иллюстрация к расчету увеличения трубы путем измерения тангенсов углов

Порядок выполнения задания 4.1

Навести трубу на стенной масштаб, находящийся от трубы на расстоянии нескольких метров, и cфокусировать ее на линейку с делениями. Отсчитывать число N делений, видимых в трубу. Одновременно вторым, невооруженным глазом смотрят мимо трубы на стенной масштаб. Добиваться того, чтобы изображение в трубе налагалось на видимый невооруженным глазом масштаб, и отметить границы поля зрения трубы (рис. 4.6).

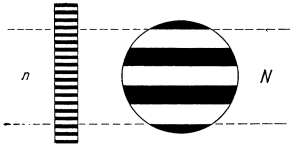
Стенной масштаб Поле зрения трубы

Рис. 4.6. Определение увеличения трубы

Всю эту операцию удобней делать вдвоем – один смотрит в трубу, другой стоит возле масштаба, отмечает границы поля зрения трубы (верхнюю и нижнюю) и считает число делений стенного масштаба n, совпадающих с делениями N его изображения, видимыми в трубу. Увеличение трубы находят по формуле

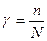(4.5)

и вычисляют погрешности. Таким способом можно производить определения увеличения только при малых увеличениях. Этот метод неточен, потому что условия опыта не соответствуют условиям применения трубы: зрительная труба применяется для наблюдения достаточно удаленных объектов

Результаты измерений и вычислений заносят в табл. 4.1.

Таблица 4.1

№ п/п	Увеличение трубы	Поле зрения трубы
Число делений шкалы, n	Число делений шкалы N, видимых в трубу	Увеличение g= n/N	Размер изображения aN, см (а – цена деления масштаба)	Расстояние от трубы до масштаба S, см	Поле зрения, 2α=57,3aN/S
Среднее значение
Погрешность

Контрольные вопросы к заданию 4.1

1. Для каких целей служит зрительная труба?

2. Как устроена зрительная труба?

3. Что называется увеличением оптической трубы?

4. Что называется полем зрения трубы?

5. Как определяется увеличение и поле зрения оптической трубы при помощи линейки?

6. Чем отличается зрительная труба Кеплера от трубы Галилея?

Задание 4.2. Определение увеличения микроскопа при помощи рисовального аппарата

Приборы и принадлежности: микроскоп; объект-микрометр; рисовальный прибор; горизонтальный миллиметровый масштаб (миллиметровая бумага на подставке); линейка масштабная.

Цель задания: экспериментальное определение увеличения микроскопа при помощи рисовального аппарата.

Дата добавления: 2015-06-04