Краткая теория. Дифракционной решетки

Дифракционной решетки

Приборы и принадлежности: источник света – He-Ne лазер (l =6328 Å); дифракционные решетки; экран с миллиметровым масштабом; измерительная линейка.

Цель задания: экспериментальное исследование распределения освещенности при дифракции света на дифракционной решетке, определение постоянной решетки.

Дифракционной решеткой называется периодическая структура, состоящая из элементов, соизмеримых (в пределах нескольких порядков) с длиной волны. Кристаллы твердых тел представляют собой трехмерную пространственную дифракционную решетку, линейные элементы, расположенные на плоскости, могут образовать плоскую решетку, ряд точек — линейную.

Прозрачные плоские дифракционные решетки изготавливаются в виде пластин из какого-либо прозрачного материла, на который алмазным резцом наносят равно отстоящие друг от друга одинаковые штрихи. Ширина прозрачного промежутка а и непрозрачного b должна быть строго постоянной для каждой решетки. Их сумма а + b = d называется постоянной, или периодом решетки.

Принципиальная схема наблюдения дифракции на прозрачной решетке представлена на рис. 6.8.

Пусть на дифракционную решетку 1 перпендикулярно ее плоскости падает пучок параллельных когерентных лучей. Решетка вызывает дифракцию световых лучей, и в фокальной плоскости 3 линзы 2 образуется сложное дифракционное изображение.

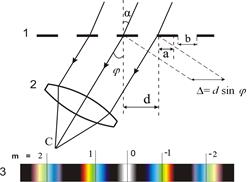
Рис. 6.8. Дифракция на дифракционной решетке

Каждая щель решетки дает дифракционную картину в полном соответствии с картиной, описанной в задании 6.1. При этом дифракционные максимумы и минимумы налагаются друг на друга. Однако теперь явление усложняется тем, что кроме дифракции от каждой щели будет происходить еще интерференция многих пучков, т. е. сложение колебаний, приходящих в данную точку от всех щелей. Если общее число щелей N, то интерферируют между собой N пучков.

Рассмотрим пучок параллельных лучей, дифрагировавших под углом j. Амплитуды колебаний, пришедших в точку С от всех щелей, будут одинаковы, обозначим через . Разность хода D между лучами от каждой из двух соседних щелей, как видно из рис.6.7, равна

D = (а + b) sin j = d sin j. (6.4)

Этой разности хода соответствует разность фаз между соседними лучами от каждых двух соседних щелей, равная

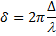. (6.5)

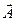Суммарную амплитуду можно представить графически вектором замыкающей ломаной линии, образованной векторами амплитуд . Очевидно, что вектор достигает максимальной величины во всех случаях, когда векторы расположены вдоль одной прямой (рис. 6.4, а). Это имеет место при d = ± 2 k p, где k = 0,1,2… При этом длина вектора 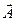равна сумме векторов амплитуд от всех щелей . Освещенность прямо пропорциональна квадрату амплитуды. Следовательно, максимальная освещенность I_max будет равна

I_max = CN²a², (6.6)

где C - коэффициент пропорциональности.

Максимумы, соответствующие условию (6.6), называются главными.

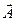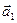Вектор становится равным 0, когда ломаная линия, образованная векторами , превращается в замкнутую линию (рис. 6.4, б), т. е. когда последний вектор направлен так же, как , но последний составляет с осью ОХ угол Nd. Следовательно, вектор будет параллелен оси ОХ при Nd = ± 2 kp, где k = 1, 2, 3 …

Таким образом, получаем условие образования минимумов

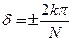. (6.7)

В минимумах освещенность I_min = 0. Нетрудно видеть, что между максимумами имеется N –1 минимум, а следовательно, еще N –2 максимума. Эти максимумы очень слабые и называются вторичными максимумами.

Приняв во внимание соотношение (6.4) и (6.5), получим, что главные максимумы возникают при значениях угла j, удовлетворяющих условию

d sin j = ± kl; k = 0,1,2. (6.8)

Рис. 6.9. Распределение освещенности при дифракции на дифракционной решетке состоящей из четырех щелей

Целое число k называют порядком спектра, выражение (6.8) - формулой дифракционной решетки. Минимумы возникают при значениях j, удовлетворяющих условию

k = 1,2,3…, (6.9)

кроме k = N, 2 N, 3 N...

Учитывая дифракцию от каждой щели и описанную ранее интерференцию от N щелей решетки, освещенность I в фокальной плоскости линзы 3 (рис. 6.8) получим в виде произведения I = I₁I₂, где I₁ - освещенность, обусловленная дифракцией на каждой щели, I₂ – освещенность, обусловленная интерференцией на решетке. На рис. 6.7 представлено истинное распределение освещенности при дифракции от четырех щелей.

Если на дифракционную решетку падает не монохроматический пучок лучей, то условия максимумов (6.7) и минимумов (6.9) будут справедливы для всех длин волн и в фокальной плоскости 3 линзы 2 (рис. 6.7) будет наблюдаться дифракционный спектр в виде смещенных максимумов для всех длин волн источника света.

Как показывает формула (6.8), в центре будет максимум нулевого порядка для всех длин волн l ₁, l ₂,…, l _n. По обе стороны от этого максимума будут располагаться максимумы 1-го, 2-го и т.д. порядков, соответственно для всех длин волн l₁, l₂,…; при этом, чем короче длина волны, тем ближе расположен соответствующий максимум к центральному. Эта картина будет дифракционным изображением, полученным в результате ограничения светового пучка дифракционной решеткой. Следовательно, дифракционная решетка – прибор, разлагающий белый свет на составные части, с ее помощью получается дифракционный спектр. Формула (6.8) позволяет определить длину волны l, если известна постоянная решетки d и порядок максимума k.

В более общем случае, когда решетка освещается немонохроматическим (сложным, например, белым) светом, дифракционная картина усложняется (рис. 6.10).

Рис. 6.10. Схематический вид дифракционного спектра

При k = 0 условие максимумов, удовлетворяется для всех длин волн, т.е. при j = 0 наблюдается центральная световая полоса, соответствующая неотклоненному пучку лучей такого цвета, каким был цвет источника.

При k = 1 симметрично по обе стороны от центральной полосы получаются дифракционные цветовые линии, от фиолетового до красного, соответствующие разным длинам волн, входящим в состав смешанного цвета. Эта группа линий называется спектрами 1-го порядка. Красная часть спектра отклонена больше, чем фиолетовая.

При k = 2 получают аналогичные спектры 2-го порядка. Линии спектров высоких порядков менее интенсивны, и на практике ясно наблюдаются спектры не выше 3-го порядка.

Рассмотрим один из методов определения длины волны при помощи дифракционной решетки. Освещая дифракционную решетку 2 (рис. 6.10) с помощью лазера 1 на расположенном за ней экране 3, можно получить четкую дифракционную картину без использования фокусирующей линзы.

Так как в установке используется монохроматическое лазерное излучение, то дифракционная картина будет представлять собой ряд ярких симметрично расположенных пятен (максимумов), интенсивность которых убывает при смещении влево и вправо от центра дифракционной картины.

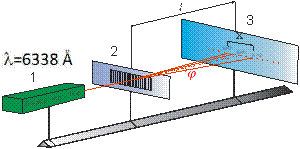
Рис. 6.10. Схема установки для определения постоянной дифракционной решетки: 1 – лазер; 2 – дифракционная решетка; 3- экран; l - расстояние от решетки до экрана; х - расстояние между центрами максимумов одноименных порядков

Для определения длины волны по формуле (6.8) необходимо знать sin j. Так как l >> х, то

sin j» tg j = .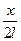

Подставляя значения в выражение (6.8), получим окончательную формулу для нахождения длины волны

. (6.10)

Длина волны измеряется в микрометрах (1 мк = 10^–6 м), нанометрах (1 нм =10^-9 м) или ангстремах (1 Å = 10^–10 м).

В данном задании необходимо вычислить постоянную дифракционной решетки, выразив ее из формулы (6.10),

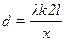(6.11)

и рассчитать число штрихов на 1 мм:

, (6.12)

значение N выражается в мм^–1. Для измерений используют две дифракционные решетки.

Порядок выполнения работы задания № 6.2

1. Включить Не-Ne лазер (l = 6328 Å) в сеть переменного тока. Установить экран на таком расстоянии от дифракционной решетки, чтобы на нем получилось четкое изображение центральной полосы и спектров 1-го и 2-го порядков.

2. Измерить расстояние от экрана до дифракционной решетки.

3. Измерить линейкой на экране расстояние между серединами красных полос спектров 1-го и 2-го порядков.

4. Значения d и N вычислить по формулам (6.11), (6.12).

5. Полученные экспериментальные данные и расчетные значения заносить в табл. 6.2. Оценить погрешности измерений.

6. Для второй дифракционной решетки заполняют аналогичную табл. 6.2.

Таблица 6.2

№ п/п	Расстояние между серединами спектров 1-го порядка х 1, мм	Расстояние между серединами спектров 2-го порядка х 1, мм	Расстояние от решетки до экрана l, мм
1-я дифракционная решетка
…
Среднее значение постоянной решетки
Число штрихов на 1 мм

Контрольные вопросы к заданию 6.2

1. Что представляет собой дифракционная решетка? Каковы параметры, характеризующие дифракционную решетку (постоянная, период, разрешающая способность, угловая и линейная дисперсия)?

2. Как выглядит дифракционная картина при дифракции на решетке? Дать качественное и количественное описание.

3. Какая связь существует между дифракцией и интерференцией?

Рекомендуемая литература: [1], [4], [11], [12], [14].

Дата добавления: 2015-06-04