Краткая теория. Приборы и принадлежности: оптическая скамья с рейтерами, бипризма, экран, микрообъектив, гелий-неоновый лазер

ОПРЕДЕЛЕНИЕ ПРЕЛОМЛЯЮЩЕГО УГЛА БИПРИЗМЫ ФРЕНЕЛЯ

Лабораторная работа 11

Приборы и принадлежности: оптическая скамья с рейтерами, бипризма, экран, микрообъектив, гелий-неоновый лазер.

Цель работы: получение интерференционной картины методом деления волнового фронта, расчет параметров интерференционной схемы.

Интерференцией называется изменение средней плотности потока энергии, обусловленное суперпозицией электромагнитных волн. Для возникновения интерференционной картины, при наложении двух или большего числа волн (т.е. чередования минимумов и максимумов интенсивности), необходимо, чтобы накладывающиеся волны были когерентными. Рассмотрим более детально это явление.

Под интенсивностью излучения I будем понимать величину, пропорциональную плотности потока энергии и равную среднему значению квадрата вектора напряженности электрического поля волны 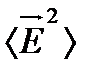. Интенсивность монохроматической гармонической волны определим соотношением

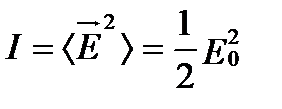, (11.1)

где E₀ – амплитуда волны.

Необходимость усреднения по времени объективно обусловлена невозможностью регистрации мгновенных значений квадрата вектора 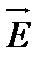. Действительно, частота электромагнитных волн оптического диапазона w ~10¹⁵с^–1, а временное разрешение (быстродействие) лучших фотоприемников t ~10^–9с, следовательно, за один измерительный цикл вектор 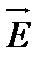совершает ~10⁶ колебаний, и результат измерений есть величина, усредненная за миллион колебаний. Кстати, все приемники излучения (в том числе и глаз) работают как квадратичные детекторы, т.е. регистрируют величины, пропорциональные второй степени E, так как при попытках регистрации усредненных за ~10⁶ колебаний значений E, меняющихся по гармоническому закону, всегда будет получаться ноль.

Пусть в некоторой точке пространства световое поле является результатом наложения двух линейно поляризованных плоских монохроматических волн

; .

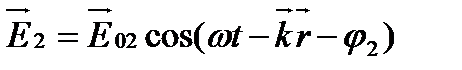Согласно принципу суперпозиции напряженность результирующего поля 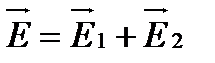. Найдем интенсивность результирующего поля, возведя предыдущее равенство в квадрат

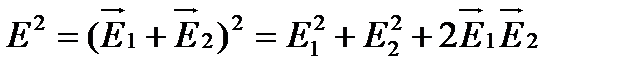(11.2)

и усредняя по времени.

При выполнении операции усреднения воспользуемся следующим известными математическими соотношениями.

1. Среднее по времени значение физической величины f(t) определяется формулой

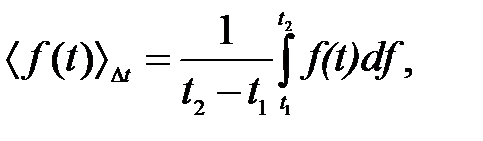(11.3)

где Dt = t₂ - t₁ – интервал усреднения.

2. Операция усреднения линейна, что следует из ее определения (11.3)

m₁f₁ + m₂f₂ = m₁f₁ + m₂f₂ = m₁ f₁ + m₂ f₂ , (11.4)

где m₁ и m₂ – постоянные.

3. Средние значения гармонических функций и их квадратов за время Dt >> T (что всегда имеет место в оптическом диапазоне) определяются соотношениями:

sin (wt + φ) = cos (wt + φ) = 0,

sin²(wt + φ) = cos²(wt + φ) =1/2. (11.5)

В справедливости последнего утверждения легко убедиться прямыми вычислениями по формуле (11.3).

Усредним по времени выражение (11.2), полагая, что радиус-вектор точки наложения волн 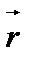=0.

(11.6)

,

,

,

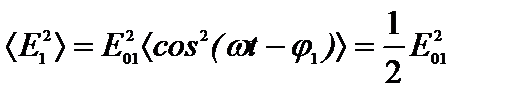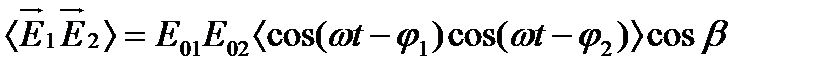где b = const – угол между векторам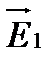и и .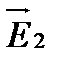

Воспользовавшись известным тригонометрическим тождеством 2 cosa×cosb = cos(a-b)+cos(a+b), преобразуем последнее выражение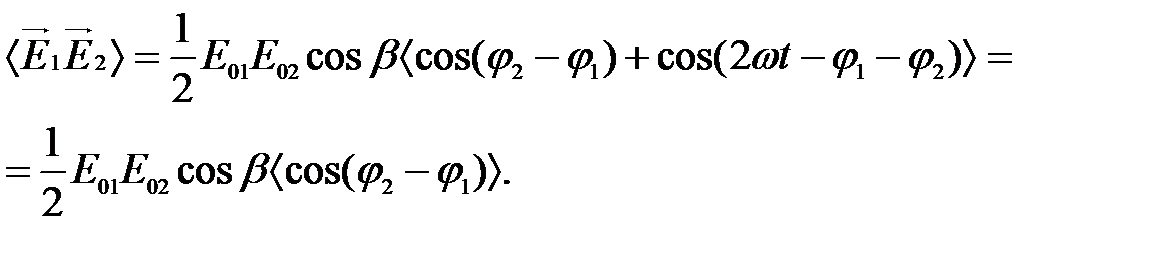

Следовательно, (11.6) может быть записана в виде:

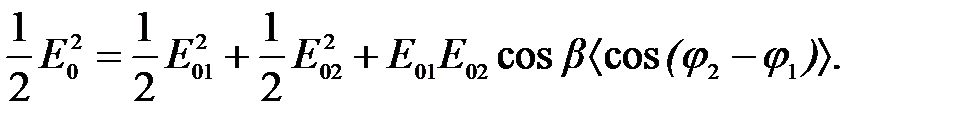
И окончательно переходя к интенсивностям волн, имеем:

(11.7)

Последнее слагаемое в правой части (11.7) называется интерференционным членом. Его наличие означает, что интенсивность электромагнитных волн в общем случае не является величиной аддитивной. Если интерференционный член в (11.7) равен нулю, то интенсивность становится аддитивной величиной I=I₁+I₂ и интерференция не наблюдается. Это возможно в двух случаях:

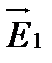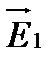1) векторы и поляризованы во взаимноперпендикулярных плоскостях, cosb = 0 (разность фаз φ ₂ – φ ₁ в этом случае может быть любой). В дальнейшем мы будем считать, что векторы и 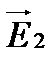поляризованы в одной плоскости и cosb = 1;

2) cosb = 1, разность фаз φ ₂ – φ ₁ меняется случайным образом, принимая с равной вероятностью любые значения, и тогда < cos (φ ₂ – φ ₁) >= 0.

Таким образом, для существования интерференции необходимо, чтобы разность фаз φ ₂ – φ ₁ сохраняла свое значение за время усреднения. Колебания, для которых разность фаз за время наблюдения остается постоянной величиной φ ₂ – φ ₁ = const, называются когерентными.

Понятие когерентности – фундаментальное понятие волновой оптики. В самом общем смысле под когерентностью следует понимать согласованное (синхронное) протекание колебательных процессов. Это понятие далеко не исчерпывается приведенным описанием, и для более глубокого понимания существа многих волновых явлений необходимо дополнительное изучение соответствующих разделов курса оптики.

Рассмотрим сложение когерентных колебаний

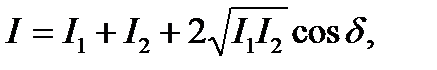(11.8)

где d= φ ₂ – φ ₁ = const.

Если 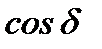= 1; d = 2 np (n = 0, ±1, ±2,….) (11.9)

,

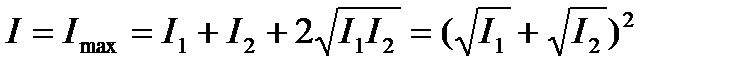если 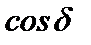= – 1; d = (2n+1)p (n = 0, ±1, ±2,….) (11.10)

.

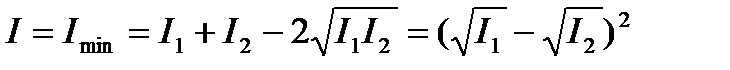При сложении волн одинаковой интенсивности I₁= I₂= I₀,

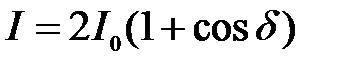(11.11)

и, следовательно, I_max=4I₀; I_min=0.

Таким образом, если волны в точку наблюдения приходят в одной фазе (точнее, разность фаз d кратна четному числу p, d=2np), наблюдается максимум интенсивности, если в противофазе (когда разность фаз d кратна нечетному числу p, d= (2n+1) p) – минимум.

Волны, пригодные для интерференции, можно получить делением одной волны на части. Это можно осуществлять двумя способами:

1) делением амплитуды волны;

2) делением фронта волны.

Части волны в отношении изменения их фазы по времени являются точными копиями исходной волны, их фазы изменяются синхронно, и, следовательно, разность фаз, оставаясь постоянной, обеспечивает их когерентность. Важно понимать, что постоянство разности фаз имеет временные и пространственные ограничения.

В данной работе рассматривается только первый способ получения интерференции. Рассмотрим интерференцию двух волн, осуществляемую делением волнового фронта, в классической схеме Юнга (рис.11.1).

Рис. 11.1. Схема опыта Юнга

Волна, испускаемая точечным монохроматическим источником S, падает на две узкие щели, которые вырезают два участка волнового фронта. Эти участки могут рассматриваться как вторичные когерентные источники S₁ и S₂, дающие при наложении на экране ОХ интерференционную картину.

Обозначим расстояние между щелями d, а расстояние от щелей до экрана – l. Найдем интенсивность светового поля в произвольной точке экрана х. Прежде всего, необходимо найти разность хода лучей l ₁и l ₂. Очевидно (по теореме Пифагора)

, ,

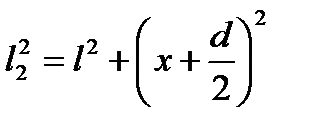следовательно, 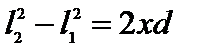, но, с другой стороны, при условии, что l>> d, 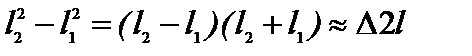, где D= l ₂ – l ₁ – геометрическая разность хода (т.е. разность длин путей, проходимых лучами до точки встречи), а значит

(11.12)

Оптической разностью хода D_опт называется величина D_опт= n ₂ l ₂ – n ₁ l ₁, где n ₁ и n ₂ – абсолютные показатели преломления сред, в которых распространяются лучи l ₁и l ₂. Будем считать, что n ₁ = n ₂=1, тогда (12) есть оптическая разность хода лучей.

В различных точках экрана в зависимости от разности хода интенсивность I светового поля может принимать любое значение от I_max до I_min.

Разность хода лучей связана с разностью их фаз очевидным соотношением

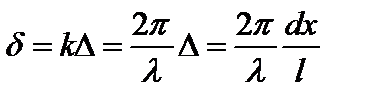, (11.13)

где k – волновое число, l – длина волны.

С учетом условий (11.9) и (11.10) можно сделать вывод, что

I=I_max, когда (n = 0, ±1, ±2,...),

I=I_min, когда 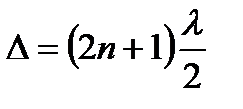(n = 0, ±1, ±2,...),

координаты точек ; .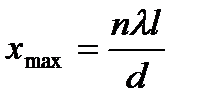

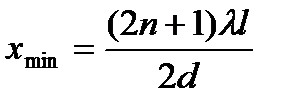Ширина интерференционной полосы D x равна расстоянию между соседними максимумами (или минимумами) интенсивности

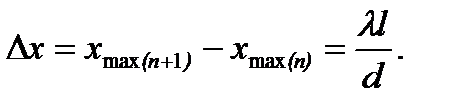(11.14)

Значение интенсивности в точке экрана с координатой x можно рассчитать по формуле (11.11) с учетом (11.13)

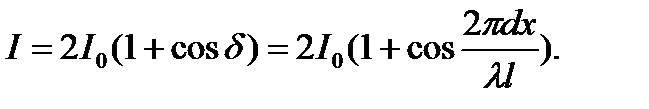(11.15)

Качественный вид функции (11.15) приведен рис. 11.1.

Следует иметь в виду, что реальные источники не являются точечными и строго монохроматическими, поэтому предложенное описание – лишь первое приближение интерференции волн от реальных источников.

Рассмотрим еще одну классическую интерференционную схему – бипризму Френеля. Эта схема используется в данной лабораторной работе.

Для разделения волны на две применяют бипризму Б с углом при вершине, близким к 180º (фактически это одна равнобедренная стеклянная призма) (рис.11.2).

Рис. 11.2. Ход лучей в схеме с бипризмой Френеля

Источником света служит ярко освещенная узкая щель S, строго параллельная преломляющему ребру бипризмы. Падающий на бипризму световой поток вследствие преломления в верхней и нижней частях бипризмы раздваивается на два луча, как бы исходящих из двух мнимых источников (щелей) S₁ и S₂. Призма может быть повернута к щели тупым углом или противоположной плоской гранью.

Так как источники S₁ и S₂ можно считать когерентными, то в пространстве за бипризмой во всей области перекрытия лучей будет иметь место интерференция. На экране Э при освещении бипризмы монохроматическим светом будет наблюдаться интерференционная картина в виде темных и светлых полос, параллельных ребру бипризмы.

Найдем ширину интерференционной полосы, воспользовавшись полученной ранее формулой (11.14) для схемы Юнга, учитывая, что в данном случае l = a + b, а расстояние между щелями d равно расстоянию между мнимыми изображениями S₁ и S₂ – d = a·2α

(11.16)

Если на бипризму падает плоская волна, т.е. a → ∞, то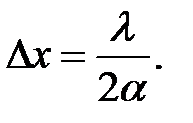

При наблюдении в белом свете центральный максимум (нулевого порядка) получается белым, остальные окрашенными, поскольку Δ х ~ λ.

Максимальное число N возможных полос интерференции на экране определяется условием N _max= x /Δ х, где x=b·2α – ширина зоны интерференции. С учетом (11.16)

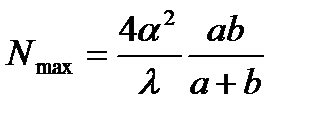. (11.17)

Поскольку преломляющий угол бипризмы θ очень мал (меньше 1º), то можно считать, что все лучи, проходящие через верхнюю и нижнюю половины бипризмы, отклоняются вниз и вверх от горизонтали на одинаковый угол

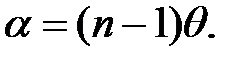(11.18)

Для доказательства этого утверждения рассмотрим ход лучей через верхнюю половину бипризмы вблизи ее основания (рис. 11.3). При выходе их призмы лучи преломляются и, если призма имеет показатель преломления n и находится в воздухе, то

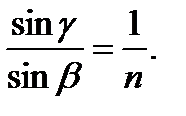
n

θ

α

γ

β

Рис. 11.3. Отклонение луча при прохождении через призму

с малым преломляющим углом θ.

Как видно из рис. 3, γ = θ (как углы с взаимно перпендикулярными сторонами), а β = γ + α = θ + α, следовательно,

,

.

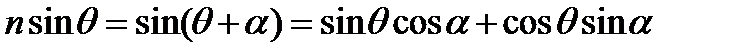Так как углы θ и α малы, то последнее равенство можно преобразовать к виду 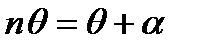или , что совпадает с (11.18).

Запишем выражения (11.16) и (11.17) с учетом (11.18):

, (11.19)

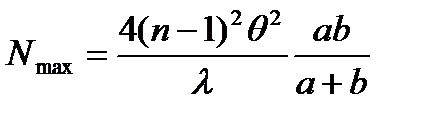. (11.20)

В заключение отметим, что при получении интерференционных картин в рассмотренных классических опытах следует обязательно учитывать роль ширины щели s (она обусловлена шириной когерентности) и степень монохроматичности λ /Δ λ (которая связана с длиной когерентности). Детальное обсуждение этих вопросов выходит за рамки данной лабораторной работы.

Можно показать (рекомендуется сделать самостоятельно), что в схеме с бипризмой Френеля для получения интерференционной картины с достаточно хорошей видимостью необходимо, чтобы ширина щели s удовлетворяла условию

, (11.21)

а степень монохроматичности – условию

. (11.22)

Дата добавления: 2015-06-04