
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Примеры решения задач. Пример 1. Используя теорему Гаусса, рассчитать напряженность электрического поля равномерно заряженной бесконечной плоскости как функцию расстояния
|
|
|
|
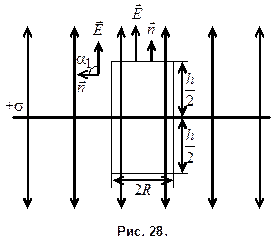 Пример 1. Используя теорему Гаусса, рассчитать напряженность электрического поля равномерно заряженной бесконечной плоскости как функцию расстояния
Пример 1. Используя теорему Гаусса, рассчитать напряженность электрического поля равномерно заряженной бесконечной плоскости как функцию расстояния 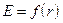 . Поверхностная плотность заряда
. Поверхностная плотность заряда  .
.
Решение.
1. Для применения теоремы Гаусса к расчету напряженности электрического поля необходимо выбрать поверхность интегрирования (Гауссову поверхность). Для этого необходимо представить картину силовых линий. Поле бесконечной заряженной плоскости, очевидно, имеет силовые линии, идущие перпендикулярно плоскости (см. рис. 28)
Форма поверхности должна учитывать симметрию поля. В нашем случае поверхность можно выбрать в виде цилиндра радиуса R, высотой h, ось которого совпадает с силовой линией. При таком выборе поверхности интегрирования поток вектора 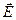 отличен от нуля только через основания цилиндра, а вдоль боковой поверхности силовые линии скользят и поток равен нулю.
отличен от нуля только через основания цилиндра, а вдоль боковой поверхности силовые линии скользят и поток равен нулю.
Запишем теорему Гаусса
 .
.
2. Вычислим поток вектора 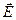 по определению
по определению
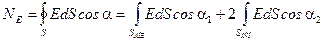 ,
,
 , так как
, так как  ,
, 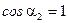 , так как
, так как 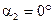 .
.
Получаем
 .
.
Модуль E вынесли за знак интеграла, т.к. все точки оснований находятся на одинаковом расстоянии от плоскости и величина E должна быть одинакова из соображений симметрии.
Окончательно  .
.
3. Найдем заряд, охватываемый поверхностью интегрирования
 .
.
4. Воспользуемся теоремой Гаусса и приравняем поток из пункта 2 к заряду найденному в пункте 3 деленному на электрическую постоянную ε0:

5. найдем из последнего уравнения напряженность
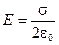 .
.
Вывод: поле бесконечной равномерно заряженной плоскости является однородным, т.е. не зависит от расстояния до заряженной поверхности.
Ответ: 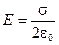 .
.
 Пример 2. В вершинах квадрата расположены одинаковые по величине заряды
Пример 2. В вершинах квадрата расположены одинаковые по величине заряды  Кл. В двух соседних вершинах расположены отрицательные заряды, а в двух других - положительные. Найти напряженность электрического поля в центре квадрата. Сторона квадрата
Кл. В двух соседних вершинах расположены отрицательные заряды, а в двух других - положительные. Найти напряженность электрического поля в центре квадрата. Сторона квадрата  см.
см.
Решение. Поле в этом случае создается системой точечных зарядов. Напряженность суммарного поля можно найти с помощью принципа суперпозиции 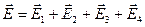 , где
, где 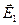 ,
,  ,
, 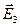 ,
,  - напряженности полей, создаваемых в центре квадрата каждым зарядом.
- напряженности полей, создаваемых в центре квадрата каждым зарядом.
Чтобы найти величину искомой напряженности необходимо спроектировать рассматриваемые вектора на оси координат. Из рис. 29 видно, что суммарная проекция на ось OX равна нулю. Вектор суммарной напряженности направлен по оси OY.
1. Запишем формулу для расчета модуля напряженности электрического поля точечного заряда
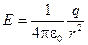 ,
,
где q - величина точечного заряда, ε0 - электрическая постоянная, r - расстояние от заряда до точки поля.
2. В нашей задаче все заряды одинаковы по модулю и расстояния от зарядов до центра квадрата также одинаковы, поэтому
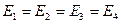 .
.
3. Найдем проекцию напряженности на оси координат:
- на ось х  ;
;
- на ось y 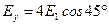 ,
,
где 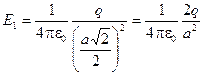 .
.
4. Получим расчетную формулу для результирующей напряженности
 .
.
5. Вычислим напряженность поля в центре квадрата
 В/м.
В/м.
Ответ:  В/м.
В/м.
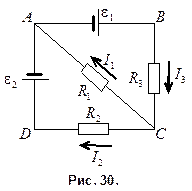 Пример 3. В схеме, приведенной на рис. 30,
Пример 3. В схеме, приведенной на рис. 30,  - элемент с ЭДС, равной 2,1 B,
- элемент с ЭДС, равной 2,1 B, 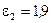 В,
В,  Ом,
Ом, 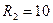 Ом,
Ом,  Ом. Найти силу тока во всех участках цепи. Внутренним сопротивлением элементов пренебречь.
Ом. Найти силу тока во всех участках цепи. Внутренним сопротивлением элементов пренебречь.
Решение. Применим правила Кирхгофа для данной разветвленной цепи.
1. Прежде всего, укажем направления токов стрелками на схеме (рис. 30). Предположим, что токи будут идти в направлении поставленных нами стрелок. По первому правилу Кирхгофа, для узла C алгебраическая сумма токов равна нулю. Токи I 1и I 2 отрицательные – они вытекают из узла
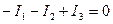 . (1)
. (1)
2. По второму правилу Кирхгофа, для контура ABC приравняем сумму падений напряжений в контуре к сумме ЭДС. Обходим по контуру по часовой стрелке.
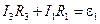 . (2)
. (2)
Аналогично для контура ACD. Обход по контуру против часовой стрелки.
 . (3)
. (3)
(Вместо контура ACD или контура ABC можно было бы взять контур ABCD.)
Имеем три уравнения для нахождения трех неизвестных  ,
,  и
и 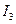 . При решении задач на применение законов Кирхгофа удобнее уравнения (1)-(3) представить в численном виде. В условиях нашей задачи эти уравнения примут вид:
. При решении задач на применение законов Кирхгофа удобнее уравнения (1)-(3) представить в численном виде. В условиях нашей задачи эти уравнения примут вид:
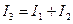 ; (1а)
; (1а)
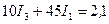 ; (1б)
; (1б)
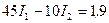 . (1в)
. (1в)
Решая эти уравнения, получим  А;
А;  А;
А;  А. Отрицательный знак у тока
А. Отрицательный знак у тока  указывает на то, что направление тока нами было взято неверно. Направление тока
указывает на то, что направление тока нами было взято неверно. Направление тока  в действительности будет от D к C, а не наоборот, как это было принято перед составлением уравнений.
в действительности будет от D к C, а не наоборот, как это было принято перед составлением уравнений.
Ответ:  А;
А;  А;
А;  А.
А.
Контрольные задания
171.  Полый стеклянный шар несет равномерно распределенный по объему заряд с объемной плотностью
Полый стеклянный шар несет равномерно распределенный по объему заряд с объемной плотностью 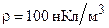 . Внутренний радиус шара
. Внутренний радиус шара  см, наружный
см, наружный  см. Вычислить напряженность E электрического поля в точках, отстоящих от центра сферы на расстоянии:
см. Вычислить напряженность E электрического поля в точках, отстоящих от центра сферы на расстоянии:  см;
см;  см и
см и 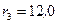 см. Построить график зависимости
см. Построить график зависимости  . Задачу решить, используя теорему Гаусса.
. Задачу решить, используя теорему Гаусса.
172. Лист стекла толщиной  равномерно заряжен по объему с объемной плотностью
равномерно заряжен по объему с объемной плотностью 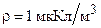 . Определить напряженность E электрического поля в точках A, B, C (рис. 30 а). Построить график зависимости
. Определить напряженность E электрического поля в точках A, B, C (рис. 30 а). Построить график зависимости  . Задачу решить, используя теорему Гаусса.
. Задачу решить, используя теорему Гаусса.
173. Бесконечная плоская пластинка толщиной 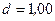 см несет заряд, равномерно распределенный по объему с объемной плотностью
см несет заряд, равномерно распределенный по объему с объемной плотностью 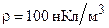 . Найти напряженность E электрического поля внутри и вне пластины. Построить график зависимости
. Найти напряженность E электрического поля внутри и вне пластины. Построить график зависимости  . Задачу решить, используя теорему Гаусса.
. Задачу решить, используя теорему Гаусса.
174. Длинный полый цилиндр радиусом  см равномерно заряжен по поверхности с поверхностной плотностью
см равномерно заряжен по поверхности с поверхностной плотностью  . Определить напряженность E электрического поля в точках, находящихся на расстояниях
. Определить напряженность E электрического поля в точках, находящихся на расстояниях  см;
см; 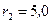 см и
см и 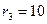 см от оси цилиндра. Построить зависимость
см от оси цилиндра. Построить зависимость  . Задачу решить, используя теорему Гаусса.
. Задачу решить, используя теорему Гаусса.
175. Доказать, что на поверхности равномерно заряженной по поверхности сферы напряженность E электрического поля такая же, какая она была бы, если весь заряд сосредоточить в центре этой сферы. Доказать, используя теорему Гаусса.
176. Найти напряженность E электрического поля в произвольной точке стеклянного шара, равномерно заряженного по объему. Начертить график  . Задачу решить, используя теорему Гаусса.
. Задачу решить, используя теорему Гаусса.
177. Определить напряженность E электрического поля, создаваемого металлической сферой радиуса 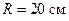 . Поверхностная плотность заряда
. Поверхностная плотность заряда  . Сфера окружена сферическим слоем диэлектрика толщиной
. Сфера окружена сферическим слоем диэлектрика толщиной 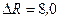 см. Начертить график зависимости
см. Начертить график зависимости  . Задачу решить, используя теорему Гаусса.
. Задачу решить, используя теорему Гаусса.
178. Найти напряженность E электрического поля, создаваемого толстостенным эбонитовым бесконечно длинным цилиндром. Внутренний радиус цилиндра  см, внешний -
см, внешний -  см. Объемная плотность заряда
см. Объемная плотность заряда  . Построить график зависимости
. Построить график зависимости  . Задачу решить, используя теорему Гаусса.
. Задачу решить, используя теорему Гаусса.
179. Найти напряженность E электрического поля, создаваемого заряженной по поверхности с поверхностной плотностью 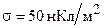 пустотелой сферой и зарядом
пустотелой сферой и зарядом  нКл, помещенным в центр этой сферы. Радиус сферы
нКл, помещенным в центр этой сферы. Радиус сферы 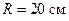 . Построить график зависимости
. Построить график зависимости  . Задачу решить, используя теорему Гаусса.
. Задачу решить, используя теорему Гаусса.
180. Рассчитайте напряженность электрического поля бесконечно длинного полого цилиндра с поверхностной плотностью заряда 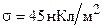 и бесконечной нитью, совпадающей с осью цилиндра, линейная плотность которой
и бесконечной нитью, совпадающей с осью цилиндра, линейная плотность которой  Кл/м. Радиус цилиндра
Кл/м. Радиус цилиндра 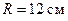 . Построить график зависимости
. Построить график зависимости  . Задачу решить, используя теорему Гаусса.
. Задачу решить, используя теорему Гаусса.
181. Две длинные одноименно заряженные нити расположены на расстоянии  друг от друга. Линейная плотность заряда на нитях
друг от друга. Линейная плотность заряда на нитях 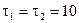 мкКл/м. Найти модуль и направление напряженности E результирующего электрического поля в точке, находящейся на расстоянии
мкКл/м. Найти модуль и направление напряженности E результирующего электрического поля в точке, находящейся на расстоянии  от каждой нити.
от каждой нити.
182. В центр квадрата, в каждой вершине которого находится заряд 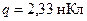 , помещен отрицательный заряд
, помещен отрицательный заряд  . Найти этот заряд, если на каждый заряд q действует результирующая сила
. Найти этот заряд, если на каждый заряд q действует результирующая сила  .
.
183. В вершинах правильного шестиугольника расположены три положительных и три отрицательных заряда. Найти напряженность E электрического поля в центре шестиугольника при различных комбинациях в расположении этих зарядов. Каждый заряд 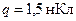 ; сторона шестиугольника
; сторона шестиугольника 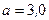 см.
см.
184. Два точечных заряда 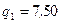 нКл и
нКл и  нКл расположены на расстоянии
нКл расположены на расстоянии 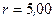 см. Найти напряженность E электрического поля в точке, находящейся на расстояниях
см. Найти напряженность E электрического поля в точке, находящейся на расстояниях 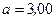 см от положительного заряда и
см от положительного заряда и 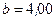 см от отрицательного заряда.
см от отрицательного заряда.
185. Найти напряженность E электрического поля в точке, лежащей посередине между точечными зарядами 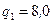 нКл и
нКл и  нКл. Расстояние между зарядами
нКл. Расстояние между зарядами  ,
,  .
.
186. Кольцо из проволоки радиусом  имеет отрицательный заряд
имеет отрицательный заряд 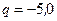 нКл. Найти напряженности E электрического поля на оси кольца в точках, расположенных от центра кольца на расстояниях L, равных 0,0; 5,0; 8,0; 10 см.
нКл. Найти напряженности E электрического поля на оси кольца в точках, расположенных от центра кольца на расстояниях L, равных 0,0; 5,0; 8,0; 10 см.
187. Найти напряженность E электрического поля на расстоянии 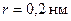 от одновалентного иона. Заряд иона считать точечным.
от одновалентного иона. Заряд иона считать точечным.
188. По тонкому кольцу радиусом  равномерно распределен заряд
равномерно распределен заряд 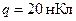 . Какова напряженность E в точке, находящейся на оси кольца на расстоянии
. Какова напряженность E в точке, находящейся на оси кольца на расстоянии 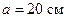 от центра кольца?
от центра кольца?
189. По тонкой нити, изогнутой по дуге окружности радиуса  равномерно распределен заряд
равномерно распределен заряд 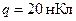 . Определить напряженность E поля, создаваемого этим зарядом в точке, совпадающей с центром кривизны дуги, если длина нити равна четверти длины окружности.
. Определить напряженность E поля, создаваемого этим зарядом в точке, совпадающей с центром кривизны дуги, если длина нити равна четверти длины окружности.
190. Построить на одном графике кривые зависимости напряженности E электрического поля от расстояния r в интервале 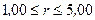 см через каждый 1,00 см, если поле образовано: а) точечным зарядом
см через каждый 1,00 см, если поле образовано: а) точечным зарядом  ; б) бесконечно длинной заряженной нитью с линейной плотностью заряда
; б) бесконечно длинной заряженной нитью с линейной плотностью заряда  ; в) бесконечно протяженной плоскостью с поверхностной плотностью заряда
; в) бесконечно протяженной плоскостью с поверхностной плотностью заряда 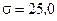 мкКл/м2.
мкКл/м2.
191. При бомбардировке неподвижного ядра натрия a-частицей сила отталкивания между ними достигла значения  . На какое наименьшее расстояние r приблизилась a-частица к ядру атома натрия? Какую скорость v имела a-частица? Влиянием электронной оболочки атома натрия пренебречь.
. На какое наименьшее расстояние r приблизилась a-частица к ядру атома натрия? Какую скорость v имела a-частица? Влиянием электронной оболочки атома натрия пренебречь.
192. До какого расстояния r могут сблизиться два электрона, если они движутся навстречу друг другу с относительной скоростью 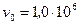 м/с?
м/с?
193. Протон (ядро атома водорода) движется со скоростью  м/с. На какое наименьшее расстояние r может приблизиться протон к ядру атома алюминия? Заряд ядра атома алюминия
м/с. На какое наименьшее расстояние r может приблизиться протон к ядру атома алюминия? Заряд ядра атома алюминия 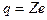 , где Z - порядковый номер атома в таблице Менделеева и e - заряд протона, равный по модулю заряду электрона. Массу протона считать равной массе атома водорода. Протон и ядро атома алюминия считать точечными зарядами. Влиянием электронной оболочки атома алюминия пренебречь.
, где Z - порядковый номер атома в таблице Менделеева и e - заряд протона, равный по модулю заряду электрона. Массу протона считать равной массе атома водорода. Протон и ядро атома алюминия считать точечными зарядами. Влиянием электронной оболочки атома алюминия пренебречь.
194. Найти потенциал j точки поля, находящейся на расстоянии 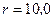 см от центра заряженного шара радиусом
см от центра заряженного шара радиусом  см. Задачу решить, если: а) задана поверхностная плотность заряда на шаре
см. Задачу решить, если: а) задана поверхностная плотность заряда на шаре  мкКл/м2; б) задан потенциал шара
мкКл/м2; б) задан потенциал шара 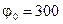 В.
В.
195. Два шарика с зарядами  нКл и
нКл и 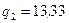 нКл находятся на расстоянии
нКл находятся на расстоянии  см. Какую работу А надо совершить, чтобы сблизить их до расстояния
см. Какую работу А надо совершить, чтобы сблизить их до расстояния  см?
см?
196. В плоском горизонтально расположенном конденсаторе, расстояние между пластинами которого  см, находится заряженная капелька массой
см, находится заряженная капелька массой 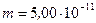 г. В отсутствие электрического поля капелька вследствие сопротивления воздуха падает с некоторой постоянной скоростью. Если к пластинам конденсатора приложена разность потенциалов
г. В отсутствие электрического поля капелька вследствие сопротивления воздуха падает с некоторой постоянной скоростью. Если к пластинам конденсатора приложена разность потенциалов 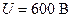 , то капелька падает вдвое медленнее. Найти заряд q капельки.
, то капелька падает вдвое медленнее. Найти заряд q капельки.
197. Электрон с энергией 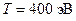 (в бесконечности) движется вдоль силовой линии по направлению к поверхности металлической заряженной сферы радиусом
(в бесконечности) движется вдоль силовой линии по направлению к поверхности металлической заряженной сферы радиусом 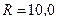 см. Определить минимальное расстояние а, на которое приблизится электрон к поверхности сферы, если заряд ее
см. Определить минимальное расстояние а, на которое приблизится электрон к поверхности сферы, если заряд ее 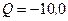 нКл.
нКл.
198. Электрон, пройдя в плоском конденсаторе путь от одной пластины до другой, приобрел скорость  м/с. Расстояние между пластинами
м/с. Расстояние между пластинами 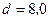 мм. Найти: 1) разность потенциалов U между пластинами; 2) поверхностную плотность заряда s на пластинах.
мм. Найти: 1) разность потенциалов U между пластинами; 2) поверхностную плотность заряда s на пластинах.
199. Пылинка массой  нг, несущая на себе
нг, несущая на себе 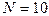 электронов, прошла в вакууме ускоряющую разность потенциалов
электронов, прошла в вакууме ускоряющую разность потенциалов  МВ. Какова кинетическая энергия Т пылинки? Какую скорость v приобрела пылинка?
МВ. Какова кинетическая энергия Т пылинки? Какую скорость v приобрела пылинка?
200. При бомбардировке неподвижного ядра калия a-частицей сила отталкивания между ними достигла  . На какое наименьшее расстояние приблизилась a-частица к ядру атома калия? Какую скорость v имела a-частица вдали от ядра? Влиянием электронной оболочки атома калия пренебречь.
. На какое наименьшее расстояние приблизилась a-частица к ядру атома калия? Какую скорость v имела a-частица вдали от ядра? Влиянием электронной оболочки атома калия пренебречь.
201.
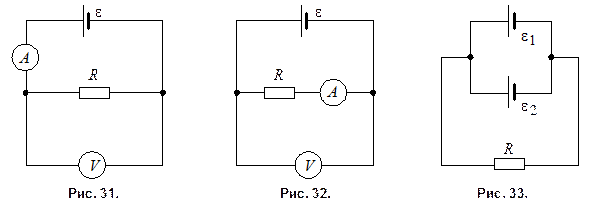 |
Считая сопротивление вольтметра
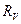 бесконечно большим, определяют сопротивление R по показаниям амперметра и вольтметра (рис. 31). Найти относительную погрешность
бесконечно большим, определяют сопротивление R по показаниям амперметра и вольтметра (рис. 31). Найти относительную погрешность 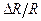 найденного сопротивления, если в действительности сопротивление вольтметра равно
найденного сопротивления, если в действительности сопротивление вольтметра равно 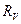 . Задачу решить для
. Задачу решить для  Ом и сопротивления: а)
Ом и сопротивления: а)  Ом; б)
Ом; б)  Ом; в)
Ом; в) 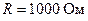 .
.
202. Считая сопротивление амперметра  бесконечно малым, определяют сопротивление R по показаниям амперметра и вольтметра (рис. 32). Найти относительную погрешность
бесконечно малым, определяют сопротивление R по показаниям амперметра и вольтметра (рис. 32). Найти относительную погрешность 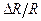 найденного сопротивления, если в действительности сопротивление амперметра равно
найденного сопротивления, если в действительности сопротивление амперметра равно  . Решить задачу для
. Решить задачу для  Ом и сопротивления: а)
Ом и сопротивления: а)  Ом; б)
Ом; б)  Ом; в)
Ом; в) 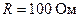 .
.
203. Два параллельно соединенных элемента с одинаковыми ЭДС 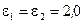 В и внутренними сопротивлениями
В и внутренними сопротивлениями  Ом и
Ом и  Ом замкнуты на внешнее сопротивление
Ом замкнуты на внешнее сопротивление  (рис. 33). Найти ток I в каждом из элементов и во всей цепи.
(рис. 33). Найти ток I в каждом из элементов и во всей цепи.
204.
 |
Два последовательно соединенных элемента с одинаковыми ЭДС
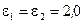 В и внутренними сопротивлениями
В и внутренними сопротивлениями  Ом и
Ом и  Ом замкнуты на внешнее сопротивление
Ом замкнуты на внешнее сопротивление  (рис. 34). Найти разность потенциалов U на зажимах каждого элемента.
(рис. 34). Найти разность потенциалов U на зажимах каждого элемента.
205.
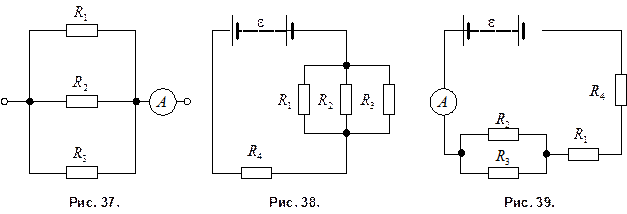 |
Батарея с ЭДС
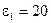 В, амперметр и реостаты с сопротивлениями
В, амперметр и реостаты с сопротивлениями 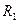 и
и  соединены последовательно (рис. 35). При выведенном реостате
соединены последовательно (рис. 35). При выведенном реостате 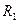 амперметр показывает ток
амперметр показывает ток 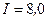 А, при введенном реостате
А, при введенном реостате 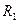 - ток
- ток  А. Найти сопротивления
А. Найти сопротивления 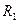 и
и  реостатов и падения потенциала
реостатов и падения потенциала 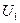 и
и 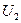 на них, когда реостат
на них, когда реостат  полностью включен.
полностью включен.
206. Элемент, амперметр и некоторое сопротивление соединены последовательно. Если взять сопротивление из медной проволоки длиной 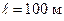 и поперечным сечением
и поперечным сечением 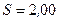 мм2, то амперметр показывает ток
мм2, то амперметр показывает ток  А. Если же взять сопротивление из алюминиевой проволоки длиной
А. Если же взять сопротивление из алюминиевой проволоки длиной 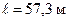 и поперечным сечением
и поперечным сечением 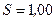 мм2, то амперметр показывает ток
мм2, то амперметр показывает ток  А. Сопротивление амперметра
А. Сопротивление амперметра  мОм. Найти ЭДС e элемента и его внутреннее сопротивление r.
мОм. Найти ЭДС e элемента и его внутреннее сопротивление r.
207. Напряжение на зажимах элемента в замкнутой цепи  , сопротивления
, сопротивления  Ом,
Ом,  Ом и
Ом и  Ом (рис. 36). Какой ток I показывает амперметр?
Ом (рис. 36). Какой ток I показывает амперметр?
208. Сопротивления  Ом и
Ом и 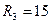 Ом (рис. 37). Через сопротивление
Ом (рис. 37). Через сопротивление 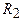 течет ток
течет ток  А. Амперметр показывает ток
А. Амперметр показывает ток 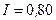 А. Найти сопротивление
А. Найти сопротивление 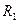 .
.
209. ЭДС батареи 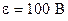 , сопротивления
, сопротивления  Ом,
Ом, 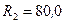 Ом и
Ом и 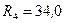 Ом (рис. 38). Найти ток
Ом (рис. 38). Найти ток  , текущий через сопротивление
, текущий через сопротивление  , и падение потенциала
, и падение потенциала 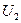 на нем.
на нем.
210. ЭДС батареи 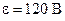 , сопротивления
, сопротивления  Ом и
Ом и  Ом (рис. 39). Падение потенциала на сопротивлении
Ом (рис. 39). Падение потенциала на сопротивлении 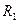 равно
равно 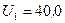 В. Амперметр показывает ток
В. Амперметр показывает ток 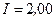 А. Найти сопротивление
А. Найти сопротивление  .
.
211. Катушка длиной  и площадью поперечного сечения
и площадью поперечного сечения  включена в цепь переменного тока частотой
включена в цепь переменного тока частотой  . Число витков катушки
. Число витков катушки 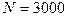 . Найти сопротивление R катушки, если сдвиг фаз между напряжением и током
. Найти сопротивление R катушки, если сдвиг фаз между напряжением и током  .
.
212. Обмотка катушки состоит из 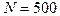 витков медной проволоки, площадь поперечного сечения которой
витков медной проволоки, площадь поперечного сечения которой 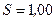 мм2. Длина катушки
мм2. Длина катушки  см, ее диаметр
см, ее диаметр  см. При какой частоте n переменного тока полное сопротивление Z катушки вдвое больше ее активного сопротивления R?
см. При какой частоте n переменного тока полное сопротивление Z катушки вдвое больше ее активного сопротивления R?
213. Два конденсатора с емкостями  мкФ и
мкФ и 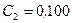 мкФ включены последовательно в цепь переменного тока напряжением
мкФ включены последовательно в цепь переменного тока напряжением 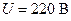 и частотой
и частотой  Гц. Найти ток I в цепи и падения потенциала
Гц. Найти ток I в цепи и падения потенциала 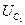 и
и  на первом и втором конденсаторах.
на первом и втором конденсаторах.
214. Конденсатор емкостью 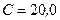 мкФ и резистор, сопротивление которого
мкФ и резистор, сопротивление которого  , включены последовательно в цепь переменного тока частотой
, включены последовательно в цепь переменного тока частотой  Гц. Какую часть напряжения U, приложенного к этой цепи, составляют падения напряжения на конденсаторе
Гц. Какую часть напряжения U, приложенного к этой цепи, составляют падения напряжения на конденсаторе  и на резисторе
и на резисторе  ?
?
215. Конденсатор и электрическая лампочка соединены последовательно и включены в цепь переменного тока напряжением  и частотой
и частотой  Гц. Какую емкость C должен иметь конденсатор для того, чтобы через лампочку протекал ток
Гц. Какую емкость C должен иметь конденсатор для того, чтобы через лампочку протекал ток  А и падение потенциала на ней было равным
А и падение потенциала на ней было равным 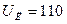 В?
В?
216. Катушка с активным сопротивлением  Ом и индуктивностью L включена в цепь переменного тока напряжением
Ом и индуктивностью L включена в цепь переменного тока напряжением 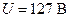 и частотой
и частотой  Гц. Найти индуктивность L катушки, если известно, что катушка поглощает мощность
Гц. Найти индуктивность L катушки, если известно, что катушка поглощает мощность 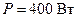 и сдвиг фаз между напряжением и током
и сдвиг фаз между напряжением и током  .
.
217. В цепь переменного тока напряжением  и частотой
и частотой  Гц включены последовательно емкость
Гц включены последовательно емкость 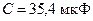 , сопротивление
, сопротивление 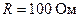 и индуктивность
и индуктивность 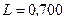 Гн. Найти ток I в цепи и падения напряжения
Гн. Найти ток I в цепи и падения напряжения  ,
,  ,
,  на емкости, сопротивлении и индуктивности.
на емкости, сопротивлении и индуктивности.
218. Индуктивность  и сопротивление R включены параллельно в цепь переменного тока частотой
и сопротивление R включены параллельно в цепь переменного тока частотой  Гц. Найти сопротивление R, если известно, что сдвиг фаз между напряжением и током
Гц. Найти сопротивление R, если известно, что сдвиг фаз между напряжением и током  .
.
219. Активное сопротивление R и индуктивность L соединены параллельно и включены в цепь переменного тока напряжением 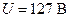 и частотой
и частотой  Гц. Найти сопротивление R и индуктивность L, если известно, что цепь поглощает мощность
Гц. Найти сопротивление R и индуктивность L, если известно, что цепь поглощает мощность  и сдвиг фаз между напряжением и током
и сдвиг фаз между напряжением и током  .
.
220. В цепь переменного тока напряжением 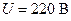 включены последовательно емкость C, сопротивление R и индуктивность L. Найти падение напряжения
включены последовательно емкость C, сопротивление R и индуктивность L. Найти падение напряжения  на сопротивлении, если известно, что падение напряжения на конденсаторе
на сопротивлении, если известно, что падение напряжения на конденсаторе 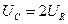 , на индуктивности
, на индуктивности  .
.
|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 7648; Нарушение авторских прав?; Мы поможем в написании вашей работы!