Соотношения неопределенностей Гейзенберга

Состояния классических частиц в ньютоновской механике и микрочастиц в квантовой физике описываются принципиально различными способами. В классической механике движение частицы описывается траекторией и в каждый момент времени частица имеет определенное положение и импульс. Поскольку микрочастицам присущи одновременно и корпускулярные и волновые свойства, то в квантовой физике в принципе нельзя говорить о траектории частицы, т.е. нельзя характеризовать мгновенное состояние микрочастицы точными заданиями ее положения и импульса.

В соответствии с гипотезой де Бройля любой частице одновременно присущи как корпускулярные, так и волновые свойства. Нетрудно убедиться, что эти два метода описания одних и тех же физических объектов во многом исключают друг друга. Например, не имеет смысла говорить о локализации монохроматической волны в пространстве, поскольку длина волны есть характеристика синусоиды, а синусоида - бесконечная периодическая кривая. Отсюда следует, что должны существовать принципиальные пределы применимости к микрочастицам понятий, характеризующих частицу в классической механике.

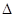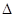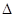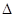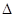Заслуга в согласовании корпускулярных и волновых свойств микрообъектов принадлежит В. Гейзенбергу. Свои результаты он сформулировал в 1927 году в виде соотношений или принципа неопределенностей. Эти соотношения определяют принципиальный предел неточностей координат x, y, z и соответствующих компонент импульса p_x, p_y, 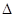p_z, с которыми состояние частицы может характеризоваться классически:

(1.21)

В соответствии с этими соотношениями следует, что чем точнее измерено положение частицы, тем с меньшей точностью можно характеризовать ее импульс, и наоборот. В частности, неопределенности импульса может и не быть (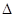 p_x = 0), как в случае свободной частицы, характеризуемой плоской волной де Бройля. Но тогда 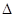x = 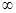, т.е. о месте, где локализована микрочастица, ничего определенного сказать нельзя. Она с равной вероятностью может быть обнаружена в любой точке пространства. Если 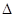x = 0, то 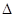p_x = 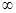В этом случае об импульсе можно высказать только вероятностное утверждение. Можно показать, что в этом случае все значения импульса равновероятны. Другими словами, если для микрочастицы точно известно ее положение в данный момент времени, то куда она будет двигаться в следующий момент времени ничего определенного сказать нельзя.

Проиллюстрируем на конкретных примерах, как с помощью соотношений неопределенностей Гейзенберга можно оценить пределы применимости к частицам понятий классической механики. Хорошо известно, что движение электрона в камере Вильсона, электронно-лучевой трубки осциллографа, кинескопа телевизора хорошо описывается законами ньютоновской механики. С другой стороны, тот же электрон в атоме водорода требует для описания своего состояния применения законов квантовой физики. Кажущееся противоречие легко объясняется с помощью количественных оценок в соответствии с соотношениями (1.21). Наблюдая трек электрона в камере Вильсона, можно лишь утверждать, что он прошел внутри капельки тумана, размер которой приблизительно 10^-6 м. Приняв это значение за неопределенность координаты электрона 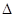x, получим для неопределенности скорости (м/с)

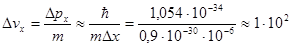
Типичные электроны, попадающие в камеру Вильсона, имеют скорости v_x ~ 10⁷  м/с. Таким образом, 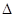v_x << v _x и неопределенность скорости не оказывает принципиального влияния на траекторию электрона.

Для электрона в атоме водорода 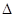x ~1 10^-10 м, 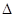v_x ~ 1 10⁶  м/с. Оценки скорости электрона в атоме водорода в рамках классической механики приводят к значениям v_x ~ 1 10⁶  м/с, т.е. в этом случае неопределенность скорости сравнима с самим значением скорости и говорить о каком-то определенном значении скорости электрона в атоме водорода не имеет смысла. Аналогичные результаты справедливы и для элементарных частиц при движении в очень малых областях пространства. Поэтому в квантовой физике при описании движений микрочастиц отказались от понятия траектории, поскольку такое понятие для этих физических объектов теряет смысл.

Оценим теперь неопределенность скорости для макроскопического тела, обладающего достаточно большой массой. Пусть это будет тело массой 1 г. Положение центра тяжести такого тела будем определять с точностью до размера атома (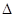 x = 1 10^-10 м). В этом случае

м/с,

т.е. для макроскопических тел неопределенность скорости настолько мала, что находится за пределами доступных способов измерений. Поэтому соотношения неопределенностей для таких тел не играют никакой роли.

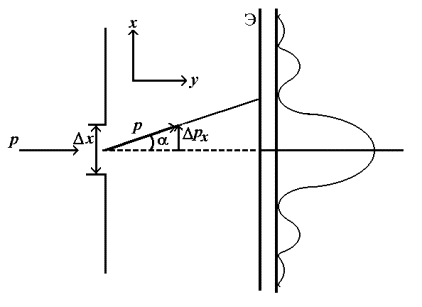
Рис.1.1. Определение положения электрона с помощью экрана со щелью

Соотношения неопределенностей Гейзенберга играют существенную роль в проблеме измерений в квантовой физике. Они устанавливают принципиальный предел точности измерений, который невозможно превзойти совершенствованием приборов и методов измерений. Любая попытка измерить, например, координату частицы приводит к искажению первоначального состояния частицы за счет взаимодействия ее с измерительным прибором, в результате чего появляется неопределенность в значении импульса. Простейшим экспериментальным прибором, позволяющим определить положение электрона, может служить узкая щель или отверстие, расположенные перпендикулярно направлению движения электрона (рис. 1.1). Направим ось x параллельно плоскости щели, а ось y - перпендикулярно к ней, как это показано на рисунке. Пусть импульс электрона до прохождения щели будет равен p, причем неопределенность x -составляющей импульса 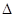p_x = 0. Если электрон прошел через щель, о чем может свидетельствовать сцинтилляция на флюоресцирующем экране Э, то его координата в момент прохождения через щель будет определена с точностью 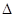x, равной ширине щели. После прохождения щели электрон вследствие явления дифракции имеет вероятность отклониться от первоначального направления движения и у него появится составляющая импульса p_x. Кривая на рис. 1.1 справа схематически описывает распределение вероятности попадания электрона на экран. Если через обозначить угол, ограничивающий положение первого дифракционного максимума на экране, то

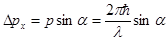
a согласно условию дифракции от щели

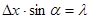
Из последних двух равенств получаем

,

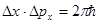что согласуется с соотношениями неопределенностей Гейзенберга.

В квантовой механике имеет место также соотношение неопределенностей Гейзенберга для времени и энергии:

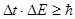(1.22)

Это соотношение означает, что чем короче время существования какого-либо состояния или время, отведенное для его наблюдения, тем с меньшей определенностью можно говорить об энергии этого состояния. Наоборот, чем больше это время, тем с большей точностью определена энергия состояния. Отсюда следует, что стационарное состояние может существовать бесконечно. Из соотношения (1.22) вытекает возможность существования виртуальных частиц, которые существуют только в состояниях, имеющих малую длительность, и не могут быть зарегистрированы. Виртуальные частицы являются переносчиками взаимодействия. Например, два электрона взаимодействуют друг с другом путем испускания одним электроном и поглощения другим виртуального фотона.

Дата добавления: 2015-06-04