Практическое использование коронного разряда

КОРОННЫЙ РАЗРЯД

Неполный пробой газового промежутка, или "огни Святого Эльма"

Коронный разряд - это неполный пробой газового промежутка. Возникает в неоднородном электрическом поле. Он может проявиться под действием атмосферного электричества на верхушках мачт, шпилей, деревьев и в других тонких и заостренных местах. В обиходе получил название "огней Святого Эльма".

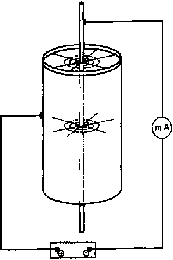
В лабораторных условиях коронный разряд легко получить, располагая тонкую проволоку внутри металлического цилиндра (Рис. 3) и создавая достаточный электрический потенциал между цилиндром и проволокой. Линии напряженности Е, направленные от внутренней поверхности цилиндра к проволоке, сгущаются в районе проволоки. Напряженность Е достигает значений 3 * 10⁶ В/м. В результате зажигается разряд (корона). При увеличении напряжения U между цилиндром и проволокой растет ток в коронном разряде и увеличивается диаметр светящейся вокруг проволоки короны.

Различают отрицательную и положительную корону по знаку электрического заряда на проволоке Электронные лавины обрываются на краю короны Расстояние, которое они проходят, и есть размеры Короны. Поэтому и возникло определение коронного разряда как неполного пробоя газового промежутка.

Механизмы возникновения отрицательной и положительной короны разные В случае отрицательной короны положительные ионы ускоряются в сильно неоднородном электрическом поле вблизи катода, чем является проволока внутри цилиндра, и выбивают из нее электроны (называется это вторичной электронной эмиссией). Выбитые электроны порождают новые положительные ионы и электронные лавины. На некотором расстоянии от проволоки электронные лавины обрываются, т.к. электрическое поле убывает с удалением от проволоки.

Таким образом, действие коронного разряда учитывается в практике строительства ЛЭП.

Люди стараются преодолеть отрицательные последствия коронного разряда, путем выбора умеренно высоких значений напряжений и используют для ЛЭП толстые провода. Имеются также случаи практического использования полезных особенностей коронного разряда. Примером является создание электрофильтров для очистки промышленных газов от твердых и жидких частиц.

Таким методом очищают, например, дым в производстве серной кислоты, очищают воздух в литейных цехах цветных металлов и в других вредных производствах. Принцип действия такого электрофильтра следующий. Внутри трубы натягивается отрицательно заряженная проволока, вокруг которой зажигается корона. Воздух внутри трубы становится сильно ионизированным. Ионы оседают на частицах дыма, поднимающихся по трубе. В результате частицы дыма приобретают такой же заряд, как коронирующая проволока, поэтому отталкиваются от нее и оседают на стенках трубы. Со стенок трубы они могут в последующем собираться, утилизоваться, либо использоваться опять в производстве, если это ценный продукт, как, например, в случае дыма в литейных цехах.

Описанный метод электрофильтрации дымов с использованием коронного разряда очень эффективен. В этом можно убедиться на простом опыте. Если прозрачную трубу с центральной проволокой заполнить темным дымом и потом включить напряжение, то воздух в трубе моментально очистится и станет светлым.

§ 14. Электростатика(Теорема Гаусса)

Поток напряженности электрического поля. Введем новую физическую величину - поток напряженности электрического поля. Напряженность поля характеризует электрическое поле в точке пространства. Поток напряженности зависит не от зависит не от значения напряженности в данной точке, а от распределения поля по поверхности той или иной площади. Именно для этой величины формулируется теорема Гаусса.
Выделим в поле элемент площадью delta S. Он должен быть настолько малым, чтобы напряженность электрического поля во всех его точках можно было считать одинаковой. Проведём нормаль п(вектор) к элементу. Направление этой нормали выбирается произвольно (рисунок 1). Угол между векторами Е и п обозначим через alfa. Тогда, по определению, потоком напряженности электрического поля Е называется произведение площади delta S поверхности на проекцию напряженности электрического поля на нормаль к элементу:
delta N = En delta S = E* delta S *соs аlfa. (10.1)
Поток может быть положительным или отрицательным в зависимости от значения угла аlfa.
рис. 1 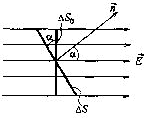рис. 2

Реально поток напряженности поля можно интерпретировать как величину, пропорциональную числу силовых линий, пронизывающих этот элемент. Линии, пронизывающие элемент delta S, пронизывают также элемент delta Sо, представляющий собой проекцию delta S на плоскость, перпендикулярную вектору Е (рисунок 2). Поток напряженности можно записать в форме:
delta N= Е*соs alfa*delta S = E delta S о, (10.2), так как delta S о = delta S*соs а.
Если поле неоднородно и поверхность произвольна, то поток определяется так. Всю поверхность надо разбить на малые элементы площадью delta S i вычислить потоки напряженности через каждый из этих элементов, а потом просуммировать потоки через все элементы (рисунок 3):
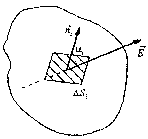рис. 3

N = е En delta S i (10.3),

Так же определяется поток через замкнутую поверхность. За положительную нормаль к любому элементу замкнутой поверхности принимается внешняя нормаль, т. е. нормаль, направленная не внутрь поверхности, а наружу.
Теорема Гаусса для точечного зарядаТеорема Гаусса устанавливает связь между потоком напряженности электрического поля через замкнутую поверхность и зарядом внутри этой поверхности.
Вначале рассмотрим простой частный случай. Вычислим поток вектора Ё в однородной среде через сферическую поверхность, в центре которой расположен точечный заряд q (рисунок 4). Напряженность поля в каждой точке на поверхности сферы одна и та же по модулю, а проекция Еп равна: Еп =k*q/er^2, Э - ипсилон (10.4) Поток вектора Е через поверхность сферы равен:
N= S En i* delta S i= En Sdelta Si= En 4pr^2= k*4pq/Э (10.5)
i
Этот результат, надо ожидать, справедлив и для любой замкнутой поверхности, содержащей заряд q. Ведь любую поверхность S1 или S2 (рисунок 4)

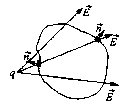рис. 4 рис.5

пронизывает то же число силовых линий, что и поверхность S. Таким образом, согласно теореме Гаусса поток напряженности через замкнутую поверхность пропорционален электрическому заряду внутри этой поверхности. теперь дадим более строгое доказательство теоремы для одного точечного заряда, охватываемого произвольной замкнутой поверхностью площадью S (рисунок 5). Выделим на этой поверхности малый элемент ее delta S. Поток напряженности через этот элемент равен:
delta N = En delta S= delta S* cos alfa* k*q/er^2, (10.6) где r - расстояние от элемента delta S до заряда q, т. е. модуль радиус-вектора, указывающего положение элемента delta S относительно заряда q. Согласно (10.2), delta S соs аlfa = delta S о, где delta S о - проекция площадки delta S на плоскость, перпендикулярную радиусу-вектору r. Так как delta S очень мала, то delta S о фактически есть проекция delta S на поверхность сферы. Следовательно, уравнение (10.6) можно переписать так:
delta N = kqdelta S о/e r^2 (10.7)
Для дальнейшего доказательства необходимо использовать понятие телесного угла.
Рассмотрим сферу радиусом r. Представим себе внутри этой сферы конус, вершина которого находится в центре сферы (рисунок 6). Этот конус вырежет на сфере некоторую часть поверхности площадью S. Область пространства, ограниченную поверхностью конуса, называют телесным углом. Мерой телесного угла w служит отношение площади S к квадрату радиуса r сферы:
рис. 6

w= S/r^2(10.8)
Нетрудно видеть, что значение телесного угла не зависит от радиуса сферы, так как площадь S вырезаемой им площадки пропорциональна квадрату радиуса. За единицу телесного угла принят стерадиан (ср) - это телесный угол с вершиной в центре сферы, вырезающий на поверхности сферы элемент, площадь которого равна квадрату радиуса сферы. Полный телесный угол, охватывающий все пространство вокруг точки, равен:
wполн= S/r^2=4pср. (10.9)
Выражение delta S о/r^2 в формуле (10.7) есть не что иное, как значение телесного угла ДО, под которым виден элемент поверхности deltaw (или, что то же самое, элемент delta S) из точки, где расположен заряд q:
deltaw= delta S о/r^2 (10.10)
Подставляя выражение (10.10) в уравнение (10.7), получим:
DeltaN=kq deltaw/e (10.11)
Суммируя подобные выражения для всех элементов deltaS; поверхности S, получим полный поток напряженности через замкнутую поверхность:
N=еdeltaNi=еdeltaw i kq/e
так как еdeltaw i = 4p ср согласно (10.9). Итак, теорему Гаусса можно записать следующим образом:

N=еdeltaNi=kq4p/e (10.12)
Если замкнутая поверхность не содержит внутри себя электрического заряда, то поток напряженности через нее равен нулю (рисунок 7). Силовые линии, идущие от заряда q, либо не пересекают ее совсем, либо же пересекают четное число раз. При этом число линий, выходящих из поверхности, равно числу линий, входящих в нее, и поэтому N = О. (Выходящие из поверхности линии вносят положительный вклад в поток, а входящие отрицательный.)
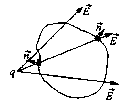рис. 7

Обобщение теоремы Гаусса
Теорема Гаусса легко обобщается на случай любого числа точечных зарядов. Поток напряженности через поверхность площадью S для каждого заряда определяется формулой (10.12). Вследствие принципа суперпозиции полей полный поток равен сумме потоков от всех зарядов. Поэтому, суммируя выражения (10.12) для всех зарядов, найдем:
N= еqi* k4p/e (10.13)
Если алгебраическая сумма зарядов внутри поверхности равна нулю, то и N = О.
Теорему Гаусса можно обобщить и для случая, когда заряд распределен в пространстве непрерывно. Это мы рассмотрим в следующем параграфе.
Коэффициент k в формуле (10.13) равен единице в абсолютной системе единиц и 1/4pe0 в СИ. Поэтому теорема Гаусса в СИ не содержит множителя 4p:
N= еqi*1/ ee0 (10.14)
Итого: теорема Гаусса связывает поток напряженности электрического поля через замкнутую поверхность с полным зарядом внутри этой поверхности.

§ 15. Электростатика(Конденсаторы)

Несмотря на довольно большой объём законов или, так скажем, "продуктов" электростатики наибольшее распространение получили лишь конденсаторы которые есть практически в любом электроприборе начиная от радиоприемника и микроволновки, и заканчивая огромными лазерами на промышленных предприятиях и турбинами на электростанциях. Вообще радиоаппаратура - это самая "известная" область применения конденсаторовда и чаще всего она-то и ассоциируется со словом конденсаторов, однако мало кто знает, что в электронно-лучевой трубке телевизора также очень много конденсаторов, и служат они для.... далее будут прдставлены в виде отдельных статей различные области применения конденсаторов

Дата добавления: 2015-06-04