III. Задачи

1. Складываются две световые волны, одинаково направленные и имеющие одинаковые периоды и амплитуды (А ₀) колебаний. Определить разность фаз, при которой результирующая волна имеет ту же амплитуду А ₀.

2. Найти все длины волн видимого света (от 0,76 до 0,38 мкм), которые будут максимально усилены при оптической разности хода интерферирующих волн, равной 1,8 мкм.

3. Вывести формулу для координаты интерференционной полосы, соответствующей минимуму, в опыте Юнга. Рассчитать расстояние между второй и первой темной полосой, если расстояние от когерентных источников до экрана 1 м, расстояние между источниками 0,2 см, а λ = 500 нм.

4. Параллельный пучок электронов, ускоренный разностью потенциалов 50 В, падает нормально на две щели, расстояние между которыми 10 мкм. Определить расстояние между центральным и первым максимумом дифракционной картины на экране, расположенном на расстоянии 0,6 м от щели.

5. В опыте Юнга на пути одного луча помещалась пластинка толщиной d ₁ = 0,11 см, а на пути другого – пластинка толщиной d ₂ = 0,1 см. Обе пластинки из стекла (n = 1,5). На сколько полос смещается интерференционная картина? Длина волны 500 нм.

6. Два когерентных источника расположены на расстоянии 2,5 мм друг от друга. На экране, расположенном на расстоянии 1 м от источника наблюдается система интерференционных полос. На какое расстояние сместятся эти полосы, если один из источников перекрыть стеклянной пластинкой (n = 1,5) толщиной 10 мкм.

7. Определить толщину плоскопараллельной стеклянной пластинки (п = 1,55), при которой в отраженном свете максимум второго порядка для λ = 0,65 мкм наблюдается под тем же углом, что и у дифракционной решетки с постоянной d = 1 мкм.

8. Монохроматический свет длины волны λ падает на стеклянный клин (n = 1,5) с углом α 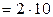^-4 рад. В наблюдаемой интерференционной картине на 1 см приходится 10 световых полос. Длина волны света равна …. нм.

9. Монохроматический свет падает нормально на поверхность воздушного клина, причем расстояние между интерференционными полосами Δ x ₁ = 0,4 мм. Определить расстояние Δ x ₂ между интерференционными полосами, если пространство между пластинками, образующими клин, заполнить прозрачной жидкостью с показателем преломления n = 1,33.

10. Между двумя плоскопараллельными стеклянными пластинами заключили очень тонкий воздушный клин. На пластинки нормально падает свет с длиной волны 500 нм. Определить угол клина, если в отраженном свете на протяжении 1 см наблюдается 20 светлых интерференционных полос.

11. На стеклянный клин (n = 1,5) падает нормально свет. Определить его длину волны, если угол клина 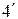и расстояние между соседними интерференционными максимумами в отраженном свете 0,2 мм.

12. Монохроматический свет падает нормально на поверхность воздушного клина, причем расстояние между интерференционными полосами 0,4 мм. Определить расстояние между полосами, если клин заполнить жидкостью с показателем преломления n = 1,33.

13. На тонкий стеклянный клиннормально к его поверхности падает монохроматический свет (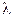 = 600 нм). Определить угол 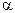между поверхностями клина, если расстояние b между соседними интерференционными максимумами в отраженном свете равно 4 мм.

14. Получить формулу и рассчитать радиус 4-го темного кольца Ньютона в отраженном свете. Радиус кривизны линзы 2,2 м, установка для наблюдения колец Ньютона освещается светом с длиной волны 495 нм.

15. Кольца Ньютона наблюдаются в отраженном свете с длиной волны 480 нм. Радиус кривизны линзы 1 м, показатель преломления стекла линзы 1,5. Между линзой и пластиной с показателем преломления 1,8 налита жидкость (n = 1,6). Определить радиус четвертого светлого кольца (мм).

16. Установка для наблюдения колец Ньютона освещается монохроматическим светом с длиной волны 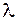= 0,6 мкм, падающим нормально. Пространство между линзой и стеклянной пластинкой заполнено жидкостью. Наблюдение ведется в проходящем свете. Радиус кривизны линзы R = 4 м. Определить показатель преломления жидкости, если радиус второго светлого кольца r = 1,8 мм.

17. Установка для наблюдения колец Ньютона освещается светом с длиной волны 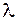= 0,6 мкм. Пространство между линзой и стеклянной пластиной заполнено жидкостью. Радиус кривизны линзы 4 м. Определите показатель преломления жидкости, если радиус второго светлого кольца 1,8 мм. Вывод формулы обосновать.

18. Установка для наблюдения колец Ньютона освещается светом с длиной волны 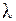= 0,6 мкм. Пространство между линзой и стеклянной пластиной заполнено жидкостью. Радиус кривизны линзы 4 м. Определите показатель преломления жидкости, если радиус второго светлого кольца 1,8 мм. Вывод формулы обосновать.

19. Определить светлое или темное кольцо Ньютона в отраженном свете имеет радиус 6,7 мм, если оно возникло при освещении светом с длиной волны 450 нм линзы радиусом кривизны 18 м (n _Л = 1,5). Между линзой и пластиной (n _ПЛ = 1,8) налит спирт (n = 1,6).

20. Установка для наблюдения колец Ньютона освещается монохроматическим светом, падающим нормально. При заполнении пространства между линзой и стеклянной пластинкой прозрачной жидкостью радиусы темных колец в отраженном свете уменьшились в 1,21 раза. Определить показатель преломления жидкости.

21. На диафрагму с круглым отверстием радиусом 1,5 мм нормально падает параллельный пучок света с длиной волны 500 нм. За диафрагмой на расстоянии 1,5 м от нее находится экран. Определить число зон Френеля на отверстии. Что будет в центре дифракционной картины на экране?

22. При помощи дифракционной решетки с периодом 0,02 мм получено первое дифракционное изображение на расстоянии 3,6 см от центрального максимума и на расстоянии 1,8 м от решетки. Найти длину волны света.

23. Максимуму пятого порядка при наблюдении в монохроматическом свете с 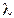= 0,5 мкм соответствует угол дифракции 30º. Определить число штрихов, которое содержит дифракционная решетка на каждый миллиметр своей длины.

24. Свет от водородной лампы падает на дифракционную решетку с периодом 2,05 мкм. Под углом 30º зарегистрирована некоторая линия десятого порядка. Определить, какому переходу электрона в атоме водорода соответствует эта линия. ().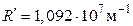

25. Дифракционная решетка, имеющая 500 штрихов на 1 мм, освещается белым светом, падающим нормально к ее поверхности. На каком расстоянии от центрального максимума находится начало и конец видимого спектра 1-го порядка (λ_Ф = 380 нм, λ_кр = 780 нм)? Экран расположен на расстоянии 2 м от решетки. (см).

26. На дифракционную решетку с периодом d, равным 0,01 мм, нормально падает свет с длиной волны 550 нм. За решеткой расположена линза с фокусным расстоянием F, равным 1 м. Определить расстояние между максимумом третьего порядка и центральным максимумом.

27. На дифракционную решетку с периодом 0,01 мм нормально падает пучок лучей от разрядной трубки, наполненной атомарным водородом. Дифракционный максимум 3-го порядка, наблюдаемый под углом 10º, соответствует одной из линий серии Бальмера. Определить квантовое число n, соответствующее энергетическому уровню, с которого совершен переход.

28. Сравнить наибольшую разрешающую способность для красной линии кадмия (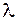 = 644 нм) для двух дифракционных решеток одинаковой длины ( 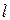= 5 мм), но разных периодов: d ₁= 4 мкм, d ₂ = 2 мкм.

29. Какое фокусное расстояние F должна иметь линза, проектирующая на экран спектр, полученный при помощи дифракционной решетки, чтобы расстояние между двумя линиями калия 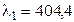нм и 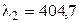нм в спектре первого порядка было равным 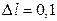мм? Постоянная дифракционной решетки 2 мкм.

30. Параллельный пучок моноэнергетических электронов направлен нормально на узкую щель шириной а = 1 мкм. Определить скорость этих электронов, если на экране, отстоящем на расстоянии l = 20 см от щели, ширина центрального дифракционного максимума составляет Δ x = 48 мкм

31. Параллельный пучок электронов, ускоренный разностью потенциалов 25 В падает на диафрагму с двумя щелями, расстояние между которыми 50 мкм. Определить расстояние между вторым и третьим максимумом на экране, расположенном на расстоянии 1 м от щелей.

32. На экран с круглым отверстием радиусом r = 1,2 мм нормально падает параллельный пучок монохроматического света с длиной волны λ = 0,6 мкм. Определить максимальное расстояние от отверстия на его оси, где еще можно наблюдать наиболее темное пятно.

33. Дифракционная решетка имеет N = 1000 штрихов и постоянную d = 10 мкм. Определить: 1) угловую дисперсию для угла дифракции φ = 30° в спектре третьего порядка; 2) разрешающую способность дифракционной решетки в спектре пятого порядка.

34. Свет падает нормально поочередно на две пластинки, изготовленные из одного и того же вещества, имеющие соответственно толщины х ₁ = 5 мм и х ₂ = 10 мм. Определить коэффициент по­глощения этого вещества, если интенсивность прошедшего света через первую пластинку составляет 82%, а через вторую – 67%.

35. Пластинка кварца толщиной d ₁ = 2 мм, вырезанная перпендикулярно оптической оси кристалла, поворачивает плоскость поляризации монохроматического света определенной длины волны на угол φ₁ = 30°. Определить толщину d ₂ кварцевой пластинки, помещенной между параллельными николями, чтобы данный монохроматический свет гасился полностью.

36. Плоскополяризованный монохроматический свет, прошедший через поляроид, оказывается полностью погашенным. Если же на пути света поместить кварцевую пластинку, то интенсивность прошедшего через поляроид света уменьшается в 3 раза (по сравнению с интенсивностью света, падающего на поляроид). Принимая удельное вращение в кварце α = 0,52 рад/мм и пренебрегая потерями света, определить минимальную толщину кварцевой пластинки.

37. На пути частично поляризованного света, степень поляризации которого 0,6, поставили анализатор так, что интенсивность света, прошедшего через него, стала максимальной. Во сколько раз уменьшится интенсивность света, если плоскость пропускания анализатора повернуть на угол .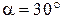

38. По пластинке длиной 3 см и шириной 1 см проходит электрический ток при напряжении 2 В. После установления теплового равновесия температура пластинки составила 1050 К. Определить силу тока, если коэффициент поглощения пластинки. а = 0,8 ().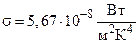

39. Металлический шар радиусом 1 см с теплоемкостью 14 Дж/К, нагретый до 1200 К, помещен в полость с температурой 0 К. Найти время остывания шара до температуры 1000 К. Шар считать абсолютно черным телом.

40. Абсолютно черное тело имеет температуру 2900 K. В результате остывания тела длина волны, на которую приходится максимум спектральной плотности излучательной способности, изменилась на 9 мкм. В сколько раз изменилась энергетическая светимость тела? Постоянная Вина .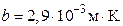

41. По пластинке длиной 3 см и шириной 1 см проходит электрический ток при напряжении 2 В. После установления теплового равновесия температура пластинки составила 1050 К. Определить силу тока, если коэффициент поглощения пластинки a = 0,8 ().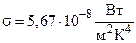

42. Принимая Солнце за черное тело, и учитывая, что его максимальной спектральной плотности энергетической светимости соответствует длина волны λ = 500 нм, определить: 1) температуру поверхности Солнца; 2) энергию, излучаемую Солнцем в виде электромагнитных волн за 10 мин; 3) массу, теряемую Солнцем за это время за счет излучения. Радиус Солнца 6,95·10⁷ м.

43. Считая, что атмосфера поглощает 10% лучистой энергии, посылаемой Солнцем, найти мощность, получаемую от Солнца горизонтальным участком земли площадью 0,5 га. Высота Солнца над горизонтом равна 30º. Излучение Солнца считать близким к излучению абсолютно черного тела с Т = 6000 К. Радиус Солнца 6,95·10⁷ м, расстояние от Земли до Солнца 1,5·10¹¹ м.

44. Температура внутренней поверхности муфельной печи при открытом отверстии площадью 30 см² равна 1,3 кК. Принимая, что отверстие печи излучает как черное тело, определить, какая часть мощности рассеивается стенками, если потребляемая печью мощность составляет 1,5 кВт.

45. В электрической лампе вольфрамовый волосок диаметром 0,05 мм накаливается при работе лампы до Т ₁ = 2700 К. Через сколько времени после выключения тока температура упадет до Т ₂ = 600 К? Считать волосок серым телом с коэффициентом поглощения 0,3. Плотность вольфрама 19300 ^кг/_м³, удельная теплоемкость 130 ^Дж/_кг·К.

46. Сколько фотонов падает за 1 мин на 1 см² поверхности Земли, перпендикулярной солнечным лучам? Солнечная постоянная w ≈ 1,4·10³ , средняя длина волны солнечного света 550 нм.

47. По пластинке длиной 3 см и шириной 1 см проходит электрический ток под напряжением 2 В. После установления теплового равновесия температура пластинки составила 1050 К. Определить силу тока, если коэффициент поглощения пластинки, а = 0,8. ().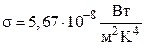

48. Диаметр вольфрамовой спирали в электрической лампочке d = 0,3 мм, длина спирали 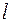= 5 см. При включении лампочки в сеть напряжением 127 В через лампочку течет ток 0,31 А. Найти температуру спирали. Считать, что все выделяющееся в нити тепло теряется на излучение. Коэффициент поглощения вольфрама 0,31.

49. Вольфрамовая нить диаметром d ₁ =0,1 мм, соединена последовательно с другой вольфрамовой нитью. Нити накаливаются в вакууме электрическим током, причем первая нить имеет температуру Т ₁ = 2000 К, а вторая Т ₂ = 3000 К. Каков диаметр второй нити?

50. Работа выхода электронов из ртути 4,53 эВ. Возникнет ли фотоэффект, если поверхность ртути осветить светом с длиной волны 500 нм? Ответ обосновать.

51. На стеклянный клин (n = 1,5) нормально падает монохроматический свет (λ = 698 нм). Определить угол между поверхностями клина, если расстояние между двумя соседними интерференционными минимумами в отраженном свете равно 2 мм.

52. При освещении металлической пластинки излучением с длиной волны 360 нм задерживающий потенциал равен 1,47 В. Определить красную границу фотоэффекта для этого металла.

53. При удвоении частоты падающего на металл света задерживающее напряжение для фотоэлектронов увеличивается в 5 раз. Частота первоначально падающего света 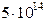Гц. Определите длину волны света, соответствующую красной границе для этого металла.

54. Фотон с длиной волны 300 нм вырывает с поверхности металла электрон, который описывает в магнитном поле (В = 1 мТл) окружность радиусом 3 мм. Найти работу выхода электрона.

55. Определить постоянную Планка, если известно, что фотоэлектроны, вырываемые с поверхности металла светом с частотой 2,8·10¹⁵ Гц, задерживаются напряжением 5,7 В, а вырываемые светом с частотой 5,2·10¹⁵ Гц – напряжением 15,64 В.

56. На 1 см² черной поверхности в единицу времени падает 2,8·10¹⁷ квантов излучения с длиной волны 400 нм. Какое давление на поверхность создает это излучение? (мкПа).

57. Свет от точечного источника, мощность которого 150 Вт, падает нормально на квадратную зеркальную площадку со стороной 10 см, расположенную на расстоянии 2 м. Определить силу давления света на площадку.

58. Лазерный пучокмощностью 600 Вт попал в кусочек идеально отражающей фольги, расположенный перпендикулярно направлению пучка. При этом кусочек фольги массой 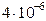кг приобрел скорость 4 см/с. Определить продолжительность лазерного импульса (с).

59. Определить давление света на стенки электрической 150-ватной лампочки, принимая, что вся потребляемая мощность пойдет на излучение, и стенки лампочки отражают 15% падающего на них света. Считать лампочку сферическим сосудом радиусом 5 см.

60. Серебряная пластинка (А _вых = 4,7 эВ) освещается светом с длиной волны 180 нм. Определить максимальный импульс, передаваемый поверхности пластины при вылете каждого электрона.

61. Определить давление света на стенки электрической 150-ваттной лампочки, принимая, что вся потребляемая мощность идет на излучение и стенки лампочки отражают 15% падающего на них света. Считать лампочку сферическим сосудом радиуса 4 см.

62. Фотон с энергией ε = 0,25 МэВ рассеялся на первоначально покоившемся свободном электроне. Определить кинетическую энергию электрона отдачи, если длина волны рассеянного фотона изменилась на 20%.

63. Фотон с энергией 0,3 МэВ рассеялся под углом θ = 180° на свободном электроне. Определить долю энергии фотона, приходящуюся на рассеянный фотон. (Λ = 0,0243Ǻ).

64. Фотон с энергией ε = 0,25 МэВ рассеялся под углом α = 120° на первоначально покоившемся свободном электроне. Определить кинетическую энергию электрона отдачи. (Λ = 0,0243Ǻ).

65. Какую скорость 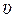приобретет первоначально покоившийся атом водорода при испускании фотона, соответствующего первой линии серии Бальмера? (.

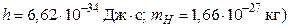66. Определить, на сколько изменились кинетическая и потенциальная энергии электрона в атоме водорода при излучении атомом фотона с длиной волны λ = 4,86·10^{-7 м.}

67. Светом, какой длины волны необходимо облучать водород, чтобы при возбуждении атомов водорода квантами этого света в спектре излучения наблюдались три спектральные линии?

68. Основываясь на том, что первый потенциал возбуждения атома водорода φ₁ = 10,2 В, определить (в эВ) энергию фотона, соответствующую второй линии серии Бальмера.

69. На дифракционную решетку с периодом 0,01 мм нормально падает пучок лучей от разрядной трубки, наполненной атомарным водородом. Дифракционный максимум 3-го порядка, наблюдаемый под углом 10º, соответствует одной из линий серии Лаймана. Определить квантовое число n, соответствующее энергетическому уровню, с которого совершен переход. R = 1,1·вектор L -момента импульса орбитального движения электрона в атоме с направлением внешнего магнитного поля. Электрон в атоме находится в d -состоянии.

70. Антикатод рентгеновской трубки покрыт молибденом (Z = 42). Определить минимальную разность потенциалов, которую надо приложить к трубке, чтобы в спектре рентгеновского излучения появились линии К-серии молибдена.

71. В атоме вольфрама электрон перешел с М -оболочки на L -оболочку. Принимая постоянную экранирования b = 5.63, определить энергию испущенного фотона.

72. Определить длину волны коротковолновой границы сплошного рентгеновского спектра, если при увеличении напряжения на рентгеновской трубке в два раза она изменилась на 50 пм.

73. Определить наименьшую длину волны рентгеновского излучения, если рентгеновская трубка работает при напряжении U = 150 кВ.

74. Используя соотношение неопределенностей, оценить E _min, которой может обладать частица массой m, находящаяся в бесконечно глубокой одномерной потенциальной яме шириной а.

75. Длина волны 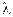излучаемого атомом фотона составляет 0,6 мкм. Принимая время жизни возбужденного состояния 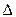t = 10^-8 c, определить отношение естественной ширины энергетического уровня, на который был возбужден атом, к энергии, излученной атомом.

76. Используя векторную модель атома, определить наименьший угол 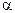, который может образовать вектор L момента импульса орбитального движения электрона в атоме с направлением внешнего магнитного поля. Электрон в атоме находится в f -состоянии.

77. Электрон в атомеводорода находится в состоянии f. Определить наименьший угол, который может образовать вектор орбитального момента импульса электрона с направлением внешнего магнитного поля.

78. Используя векторную модель атома, определить наименьший угол, который может образовать вектор орбитального момента импульса электрона в атоме с направлением магнитного поля. Электроны находятся в d -состоянии.

79. Электрон находится в бесконечно глубокой одномерной потенциальной яме шириной 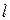. Вычислить вероятность того, что электрон, находящийся в возбужденном состоянии (n = 4) будет обнаружен в левой крайней четверти ямы.

80. Заряженная частица, ускоренная разностью потенциалов U = 200 В, имеет длину волны де-Бройля 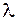= 2,02 пм. Найти массу частицы, если ее заряд численно равен заряду электрона.

81. Длина волны де-Бройля протона, летевшего с энергией 2 МэВ, увеличилась в 2 раза. Определить, какую энергию потерял при этом протон.

82. Пользуясь теорией Бора, получить выражение для радиуса орбиты электрона. Рассчитать радиус ближайшей к ядру орбиты электроны в атоме водорода.

83. Определить длину волны де-Бройля электронов, при соударении с которыми в видимой серии атома водорода появилась одна линия.

84. Определить длину волны де-Бройля электронов, при соударении с которыми в спектре атома водорода появились только 3 линии.

85. Какова длина волны де-Бройля электронов, при соударении с которыми в спектре атомов водорода наблюдаются три спектральные линии в серии Бальмера.

().

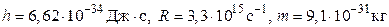86. Определить длину волны де-Бройля электронов, при бомбардировке которыми невозбужденных атомов водорода в их спектре появились две линии в первой инфракрасной серии.

().

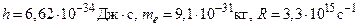87. Фотон с энергией 3 МэВ в поле тяжелого ядра превратился в пару электрон-позитрон. Если скорости этих частиц одинаковы, то какова их кинетическая энергия в МэВ? ().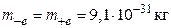

88. Найти массу урана-238, имеющего такую же активность, как и стронций-90 массой 1 мг. Периоды полураспада урана и стронция соответственно 4·10⁹ и 28 лет.

89. Препарат массой 10^{-6 кг помещен в калориметр с теплоёмкостью 8 Дж/К. После 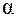-распада он превращается в изотоп свинца 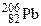. На сколько поднимется температура в калориметре за 1 час? Период полураспада 138 суток. (массы изотопов: 209,982887 а.е.м., 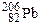205,97447 а.е.м, 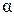- частицы 4,002609 а.е.м.).}

90. Атомная электростанция, имеющая КПД 25% расходует в сутки 235 г урана-235. Определите мощность станции, если при делении одного ядра урана выделяется 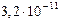Дж энергии.

91. КПД атомной электростанции 20%. При делении одного ядра 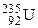выделяется 200 МэВ энергии. Сколько урана расходуется за 1 час работы электростанции мощностью 10⁶ Вт.

92. Счетчик Гейгера, установленный вблизи препарата радиоактивного изотопа серебра регистрирует поток 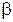-частиц. При первом измерении поток Ф₁ частиц был равен 87 с^-1, а по истечении времени t = 1 сут поток Ф₂ оказался равным 22 с^-1. Определить период полураспада Т _1/2 изотопа.

93. Определить удельную энергию связи изотопа кислорода 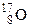. (масса нейтрона 1,00867 a.e.м., масса атома водорода 1,00783 a.e.м., масса атома кислорода 16, 99913 a.e.м.). (МэВ).

94. Определить суточный расход чистого урана 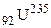атомной электростанцией тепловой мощностью Р = 300 МВт, если энергия Е, выделяющаяся при одном акте деления ядра урана составляет 200 МэВ.

95. КПД атомной электростанции 20%. При делении одного ядра 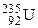выделяется 200 МэВ энергии. Сколько урана расходуется за 1 час работы электростанции мощностью 10⁶ Вт?

96. Атомная электростанция, имеющая КПД 25% расходует в сутки 235 г урана-235. Определите мощность станции, если при делении одного ядра урана выделяется 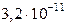Дж энергии.

97. КПД атомной электростанции мощностью 5000 кВт – 17%. При делении одного ядра 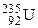выделяется энергия 200 МэВ. Какое количество урана (г) расходует электростанция за сутки? ().

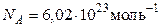98. Препарат 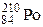массой 10^{-6 кг помещен в калориметр с теплоёмкостью 8 Дж/К. После 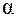-распада он превращается в изотоп свинца 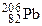. На сколько поднимется температура за 1 час? Период полураспада 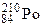138 суток. (массы изотопов: 209,982887 а.е.м., 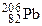205,97447 а.е.м, 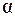-частицы 4,002609 а.е.м.).}

99. Определить число атомов, распадающихся в радиоактивном изотопе за время t = 1 c, если его активность А = 0,1 МБк. Считать активность постоянной в течение указанного времени.

Дата добавления: 2015-06-04