Уравнение критичности для реактора конечных размеров

Значение величин λ, υ, μ, φ, Θ, r позволяет определить к_∞(коэффициент размножения в бесконечной среде). Для реактора конечных размеров к_эфф< к_∞ из-за утечки в процессе замедления и диффузии. Вероятность избежать утечки в процессе замедления

,

в процессе диффузии

,

где 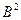,(1/см²)-геометрический параметр, который зависит от формы и размеров активной зоны. Для

сферы с R: ,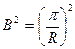

цилиндра R и Н: ,

Полная вероятность того,что избежит утечки 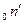из реактора в процессе замедления и диффузии

Так как увеличение размеров активной зоны геометрические параметры уменьшаются, то вместе с этим увеличивается вероятность избежания утечки в процессах замедления и диффузии, то есть меньшая доля нейтронов покидает активную зону. Физически - объясняется уменьшением отношения поверхности активной зоны к объему с увеличением ее размеров.

Т.к

к_эфф= к_∞∙Р,то

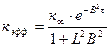
Для бесконечной среды к_∞=1,для реактора конечных размеров к_эфф=1,что является условием критичности для реактора конечных размеров

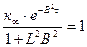
Последнее уравнение позволяет определить критические размеры активной зоны (без отражателя) заданного состава и заданной геометрической формы. Сначала из него определяют В², которое зависит от к_эфф, к_∞ и τ, определяемых в свою очередь составом и структурой активной зоны. Поэтому В² называют материальным параметром. Затем он приравнивается к геометрическому параметру и по их формулам определяются критические размеры. Для сферы просто определить R, а для других форм необходимо задаться определенными соотношениями между размерами, которые целесообразно выбирать из условия обеспечения наименьшей критической массы.

Утечка нейтронов зависит от отношения поверхности активной зоны к ее объему. Поэтому наименьшая критическая масса для активной зоны определенного объема и определенного состава имеет место при наименьшем значении поверхности активной зоны.

Зная наивыгоднейшее соотношение между размерами, можно найти зависимость минимального критического объема от величины материального параметра, равного в критическом реакторе геометрическому параметру.

Для цилиндрической активной зоны:

,

для сферы:

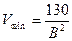
Для сферы наименьшее, так как сфера имеет наименьшую поверхность.

Уравнение критичности может быть значительно упрощено для случая больших реакторов. Большими считаются реакторы, для которых 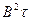‹‹1, то есть ‹‹1 или R›› .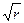

Отсюда видно, что большими реакторами являются такие, у которых размеры активной зоны намного больше длины замедления.

Тогда при удовлетворении неравенства 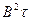‹‹1 получим

, где М²= L²+ r –площадь миграции.

Кроме определения критических размеров важное практическое значение имеет и другая задача- расчет эффективного коэффициента для активной зоны определенных состава, формы и размеров. Для этого используют уравнение

,

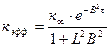в которое с этой целью вместо В² подставляется рассчитанное для данного реактора значение геометрического параметра.

В расчетах реакторов встречается и обратная задача- определение размеров активной зоны определенного состава и геометрической формы, которые обеспечивают необходимое значение к_эфф, найденное из условия обеспечения заданной продолжительности работы реактора. Для этого из уравнения к_эфф при выбранном значении к_эфф находят материальный параметр В² и приравнивают его к геометрическому параметру. Из этого последнего уравнения и определяются требуемые размеры активной зоны.

Уравнение критичности позволяет обнаружить зависимость критических размеров активно зоны от площади миграции. Из этого уравнения следует, что с увеличением L и τ материальный параметр уменьшается и следовательно, уменьшается равный ему геометрический параметр. А это означает, что критические размеры реактора возрастают. Данный результат физически вполне очевиден.

Действительно τ характеризует расстояние по прямой, на которое смещается 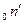в процессе своего замедления до тепловой энергии, а L² характеризует расстояние, пройденное тепловым 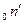до точки захвата. Чем больше эти расстояния, тем меньше вероятность того, что нейтрон избежит утечки в процессе диффузии и замедления, то есть тем больше размеры реактора, при которых протекает самоподдерживающаяся цепная реакция.

Например, реактор, где в качестве замедлителя- вода при прочих равных условиях будет иметь гораздо меньше размеры, чем реактор с графитовым замедлителем, так как для воды L=2,72см, τ= 31см, а для графита L=58см, τ= 313см. Вследствие высокого содержания Н₂ органические жидкости приближаются к воде по замедляющим и диффузионным качествам. Поэтому реактор с органическим замедлителем имеют малые габариты.

Дата добавления: 2015-06-04