Геодезическая основа географических карт

Модели Земного шара.

Основы картографии.

ОДНОСУСТАВНЫЕ И ДВУСУСТАВНЫЕ МЫШЦЫ

ТЕРМИНЫ ДЛЯ ОБЪЯСНЕНИЯ ПОЛОЖЕНИЯ ТАЗА

Тяга горизонтального блока

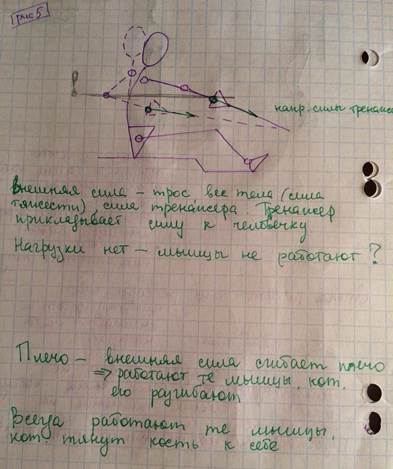Движения, которые может выполнить бицепс бедра:

- сгибание голени

- разгибание таза

- разгибание бедра

-

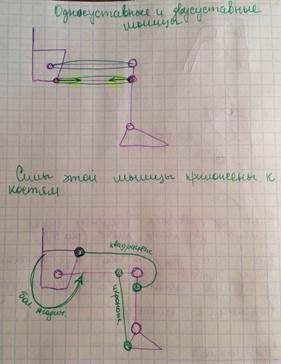Карта – это уменьшенное, обобщенное, обобщенное условное изображение Земной поверхности, построенное по определенным математическим законам. Эти законы определяют как отображать Земной шар, являющийся объемным телом сложной формы близкой к шару на плоскости.

Математическую основу географических карт составляют три элемента:

1.) выбранный эллипсоид или геодезическая основа,

2) масштаб

3) картографическая проекция.

Рассмотрим каждое из этих понятий.

Представление о том, что Земля имеет сферическую форму, по-видимому, возникли в древней Греции с VI-V в. до н.э. Дошедшие произведения более поздних античных источников приписывают эту идею разным авторам Анаксимандру, Пифагору, Пармениду. К VI-III вв. до н.э. относятся и первые данные о размерах Земли. Аристотель в своей книге «О небе» приводит значение длины окружности Земли в 400000 стадий, которое примерно в два раза превышает современное значение[1]. Более точно значение этой величины в 250000 стадий определил Эратосфен[2].

Далее вплоть до конца XVII века труды ученых Востока и Запада позволили получить более точные размеры Земли, однако представление о ней как о шаре оставалось неизменным. Здесь можно отметить труды китайского астронома И-Синь (683 -727 гг.) времен правления династии Тан, работы выполненные по повелению багдадский халифа Абу-ль-Аббас Абд-Аллах аль-Маму́н (786-833 гг.) из династии Аббасидов, работы выдающегося узбекского ученого-энциклопедиста Бируни (Беруни) Абу Райхан (973-1048 гг.). В результате этих исследование наряду с другими результатами были получены более точные значение длины дуги градуса земного меридиана.

Дальнейее уточнение длины градуса было проведено несколькими европейскими учеными

В 1528 г. Жан Фернель (не путать с выдающимся физиком Огюстен Жан Френелем) подсчитал число оборотов колеса экипажа от Парижа до Амьена, которому соответсвовало изменение широты на 1 градус и получил значение длины дуги 110,6 км

В 1615 г. голландский ученый Виллеброрд Снеллиус с помощью изобретенного им метода триангуляции определил длину меридиана между Алькмаром и Бергеном и получил значение 107335 м. Другими учеными был выполнен еще рад аналогичных исследований.

Особое место в подобных исследованиях заняла работа члена Парижской академии Жана Пикара, выполненная в 1669-1670 гг. Он впервые использовал в угломерных инструментах вместо диоптров[3] зрительные трубы и получил значение длины дуги градуса меридиана (тоже между Парижем и Амьеном) 111210 м, что лишь на 30 м больше значения, определяемого в наше время. Он же первый высказал предположение, что Земля не является шаром.

Следующий этап развития представлений о форме земли связан с именем И. Ньютона, поставившего задачу о равновесной формы гравитирующей жидкости, вращающейся вокруг оси, и показавшего, что эта форма – эллипсоид вращения. Это в свою очередь дало толчок к работе многих математиков XVIII-XIX вв. по изучению возможных форм вращающихся тел, находящихся в равновесии (К. Маклорен, Т. Симпсон, А. Клеро, А. Лежандр, П. Лапласа, С. Пуассона, Л. Эйлера, Ж. Лагранжа, К. Якоби, А. Ляпунов, А. Пуанкаре). Их работы показали что это могут быть не только эллипсоиды вращения (исследованные Маклореном), но и трёхосные эллипсоиды общего вида, (эллипсоиды Якоби).

В XVIII были выполнены и важнейшие практические исследования, подтвердившие, что земля не является шаром. В 30-е годы XVIII века французской Академией наук были снаряжены две экспедиции, задачей которых было определение длины градуса на полярном круге и на экваторе.

Одна из этих экспедиций под руководством Пьер-Мари Мопертюи, работала в Лапландии. Вторая экспедиция, изначально руководимая академиком Годена, а в ходе работ также Буге, и Лакондамином провела измерение длины дуги градуса в Южной Америке в Перу. Результаты показали, что длина дуги градуса у полярного круга и примерно на 1300 м больше, чем близ экватора, что свидетельствует о сплющенности Земли на полюсах.

Итак в конце XVII - начале XVIII века, было теоретически обосновано, и экспериментально проверено, что хотя Земля и близка по форме к шару но более точно ее форму описывает эллипсоиду вращения.

Перейдем к теперь к современным представлениям. В настоящее время для описания формы Земли используется понятие «геоид». Этот термин был предложен в 1873 году немецким математиком Иоганном Бенедиктом Листингом для обозначения геометрической фигуры, более точно отражающей форму Земли, чем эллипсоид вращения.

Геоид – фигура сложной формы (рис. 1.1). Его поверхность совпадает с поверхностью морей и океанов в их спокойном состоянии и ее мысленным продолжением под материками. Эта поверхность во всех точках перпендикулярна силе тяжести.

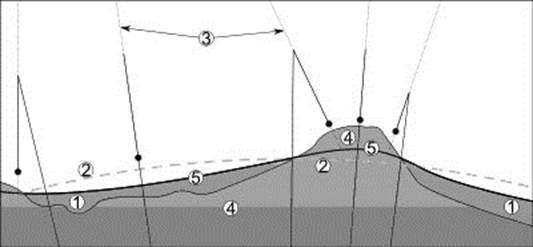
Рис. 1.1. Расположение геоида и земного эллипсоида относительно тела земли.

1. Мировой океан. 2. Земной эллипсоид. 3. Отвесные линии. 4. Тело Земли. 5. Геоид.

Поверхность геоида не является геометрически правильной фигурой и работать с такой фигурой очень сложно, поэтому в картографии вместо геоида используют эллипсоидом вращения –фигурой, получаемой вращением эллипса вокруг одной из его осей (рис 1.2).

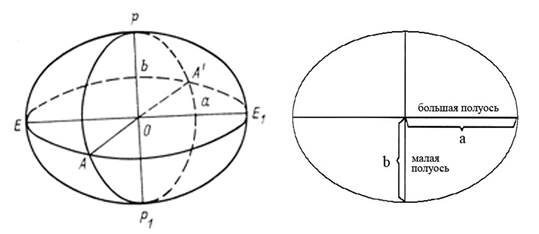
Рис 1.2. Эллипсоид и его параметры.

Форма и размеры земного эллипсоида характеризуются большой а и малой b полуосями, а чаще большой полуосью а и полярным сжатием α=(a-b)/a,

Параметры эллипсоида выбирают так, чтобы среднеквадратичное отклонение от поверхности геоида было минимальным для всей поверхности Земли, либо для заданной территории. В последнем случае эллипсоид называют референц-эллипсоидом (рис 1.3).

Рис 1.3. Определение среднего земного эллипсоида и референц-эллипсоида для заданной территории

Определением параметров земного эллипсоида ученые многих стран занимаются в течении уже более двух веков. В таблице 1.1 приведены параметры некоторых используемых в мире эллипсоидов.

Табл. 1.1. Параметры некоторых эллипсоидов, используемых в картографии.

Эллипсоиды	Полуоси	Сжатие α=(a-b)/a	Страны
a	b
Бесселя 1841 г.	637739,155*		1/299,1528128	Европа и Азия
Кларка 1866 г.	6 378206,4		1/294,9786982	Сев. и центральная Америка
Кларка 1880 г.	6 378 249,145		1/293,465	Африка, Барбадос, Израиль, Иордания, Иран, ямайка
Хейфорда 1909 г.	6 378388		1/297,0	Европа, Азия, Ю. Америка, Антарктида
Красовского 1940 г		6356863,0188	1/298,3	Россия, страны СНГ, восточно-европейские страны, Антарктида
Геодезическая референц-система 1980 г. (GRS80)	6 378 137		1/298,257222101
Всемирная геодезическая система 1984 г.(WGS84)	6 378 137		1/298,257223563
ПЗ90			1/298,25784	Россия
IERS96	6378136,49		1/298,25645

Данные эллипсоиды использовались, а некоторые и используются до настоящего времени для топографо-геодезических и картографических в работ разных стран.

Эллипсоид Бесселя применялся в Германии и ряде других стран, а также в Советском Союзе вплоть до 1942 г., когда начался переход к эллипсоиду Красовского.

Эллипсоид Кларка (1866 г.) применяется в США, странах Латинской и Центральной Америки, включая Кубу, а также в ряде других стран.

Эллипсоид Хейфорда используется в ряде европейских стран. Он в 1942 г. в Мадриде на II Генеральной ассамблее Международной ассоциации геодезии был рекомендован в качестве международного.

Эллипсоид (референц-эллипсоид) Ф.Н. Красовского – принят с 1946 г. для всех работ на территории бывшего СССР, является наиболее точным из всех эллипсоидов, полученных из обработки наземных измерений. Его размеры близки к размерам общего земного эллипсоида, полученным по данным наблюдений искусственных спутников земли.

Эллипсоид GRS80 (Geodetic Reference System 1980) разработан Международной Ассоциацией Геодезии и Геофизики (International Union of Geodesy and Geophysics) и рекомендован для геодезических работ;

Дата добавления: 2015-06-04