
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Введение. Пользуясь формулой Ньютона-Лейбница, вычислите интеграл
|
|
|
|
Пользуясь формулой Ньютона-Лейбница, вычислите интеграл.
Пользуясь формулой Коши для производных, вычислите интеграл.
Пользуясь интегральной формулой Коши, вычислите интеграл.
1) а)  ; б)
; б) 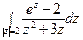 .
.
2) а)  ; б)
; б) 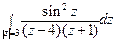 .
.
3) а) 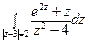 ; б)
; б) 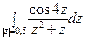 .
.
4) а)  ; б)
; б) 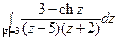 .
.
5) а) 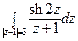 ; б)
; б)  .
.
6) а) 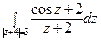 ; б)
; б) 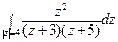 .
.
7) а)  ; б)
; б)  .
.
8) а)  ; б)
; б)  .
.
9) а)  ; б)
; б)  .
.
10) а)  ; б)
; б) 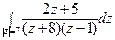 .
.
11) а)  ; б)
; б) 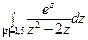 .
.
12) а)  ; б)
; б)  .
.
13) а)  ; б)
; б)  .
.
14) а)  ; б)
; б)  .
.
15) а)  ; б)
; б)  .
.
16) а) 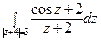 ; б)
; б) 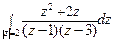 .
.
17) а) 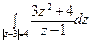 ; б)
; б)  .
.
18) а)  ; б)
; б) 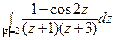 .
.
19) а) 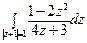 ; б)
; б)  .
.
20) а)  ; б)
; б)  .
.
21) а) 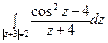 ; б)
; б)  .
.
22) а) 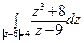 ; б)
; б) 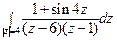 .
.
23) а)  ; б)
; б)  .
.
24) а)  ; б)
; б) 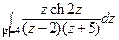 .
.
25) а)  ; б)
; б) 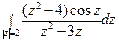 .
.
26) а) 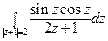 ; б)
; б)  .
.
27) а) 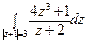 ; б)
; б)  .
.
28) а)  ; б)
; б)  .
.
29) а)  ; б)
; б)  .
.
30) а)  ; б)
; б) 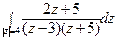 .
.
1) а) 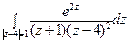 ; б)
; б) 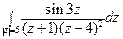 .
.
2) а) 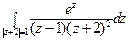 ; б)
; б) 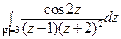 .
.
3) а) 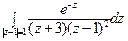 ; б)
; б) 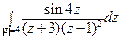 .
.
4) а) 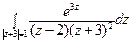 ; б)
; б) 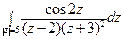 .
.
5) а) 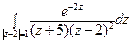 ; б)
; б) 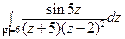 .
.
6) а) 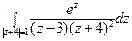 ; б)
; б) 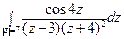 .
.
7) а) 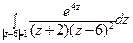 ; б)
; б) 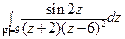 .
.
8) а) 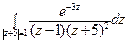 ; б)
; б) 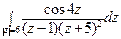 .
.
9) а) 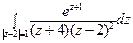 ; б)
; б) 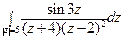 .
.
10) а) 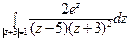 ; б)
; б) 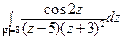 .
.
11) а) 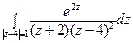 ; б)
; б) 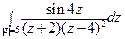 .
.
12) а)  ; б)
; б) 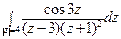 .
.
13) а) 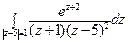 ; б)
; б) 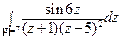 .
.
14) а) 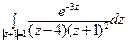 ; б)
; б) 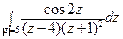 .
.
15) а) 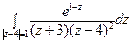 ; б)
; б) 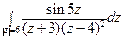 .
.
16) а) 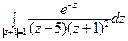 ; б)
; б) 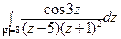 .
.
17) а) 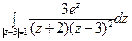 ; б)
; б) 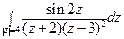 .
.
18) а) 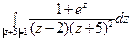 ; б)
; б) 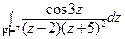 .
.
19) а) 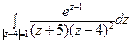 ; б)
; б) 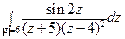 .
.
20) а) 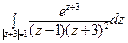 ; б)
; б) 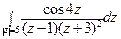 .
.
21) а) 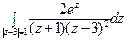 ; б)
; б) 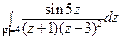 .
.
22) а) 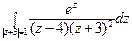 ; б)
; б) 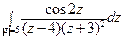 .
.
23) а) 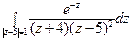 ; б)
; б) 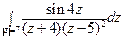 .
.
24) а) 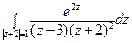 ; б)
; б) 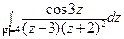 .
.
25) а) 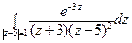 ; б)
; б) 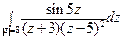 .
.
26) а) 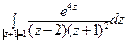 ; б)
; б) 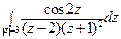 .
.
27) а) 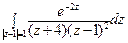 ; б)
; б) 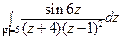 .
.
28) а) 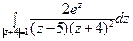 ; б)
; б) 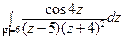 .
.
29) а) 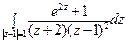 ; б)
; б) 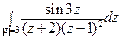 .
.
30) а) 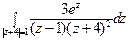 ; б)
; б) 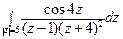 .
.
1) 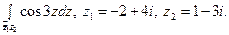
2) 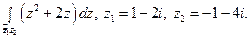
3) 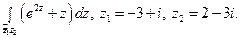
4) 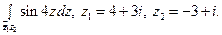
5) 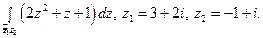
6) 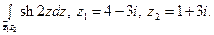
7) 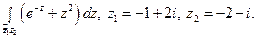
8) 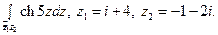
9) 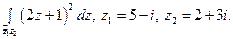
10) 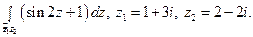
11) 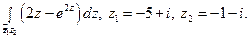
12) 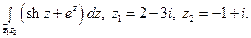
13) 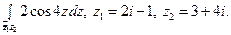
14) 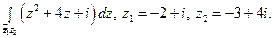
15) 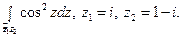
16) 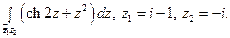
17) 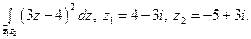
18) 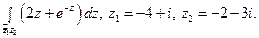
19) 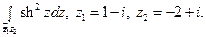
20) 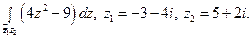
21) 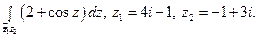
22) 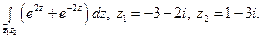
23) 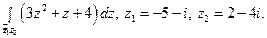
24) 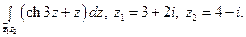
25) 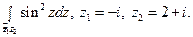
26) 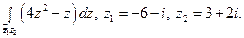
27) 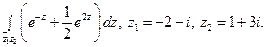
28) 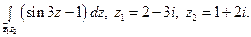
29) 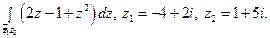
30) 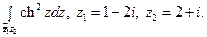
Теория нейронных сетей возникла из исследований в области искусственного интеллекта, а именно из попыток воспроизвести способность нервных биологических систем обучаться и исправлять ошибки, моделируя низкоуровневую структуру мозга. Основой исследований по искусственному интеллекту в 60–80-е гг. были экспертные системы. Такие системы основывались на высокоуровневом моделировании процесса мышления (в частности, на представлении, что процесс нашего мышления построен на манипуляциях с символами).
Теория нейронных сетей включают широкий круг вопросов из разных областей науки: биофизики, математики, информатики, схемотехники и технологии. Поэтому понятие "нейронные сети" детально определить сложно.
Искусственные нейронные сети (НС) — совокупность моделей биологических нейронных сетей.
Представляют собой сеть элементов — искусственных нейронов — связанных между собой синоптическими соединениями. Сеть обрабатывает входную информацию и в процессе изменения своего состояния во времени формирует совокупность выходных сигналов. Работа сети состоит в преобразовании входных сигналов во времени, в результате чего меняется внутреннее состояние сети и формируются выходные воздействия. Обычно НС оперирует цифровыми, а не символьными величинами.
Применение нейронных сетей:
Распознавание образов и классификация
В качестве образов могут выступать различные по своей природе объекты: символы текста, изображения, образцы звуков и т. д. При обучении сети предлагаются различные образцы образов с указанием того, к какому классу они относятся. Образец, как правило, представляется как вектор значений признаков. При этом совокупность всех признаков должна однозначно определять класс, к которому относится образец. В случае, если признаков недостаточно, сеть может соотнести один и тот же образец с несколькими классами, что неверно. По окончании обучения сети ей можно предъявлять неизвестные ранее образы и получать ответ о принадлежности к определённому классу.
Топология такой сети характеризуется тем, что количество нейронов в выходном слое, как правило, равно количеству определяемых классов. При этом устанавливается соответствие между выходом нейронной сети и классом, который он представляет. Когда сети предъявляется некий образ, на одном из её выходов должен появиться признак того, что образ принадлежит этому классу. В то же время на других выходах должен быть признак того, что образ данному классу не принадлежит. Если на двух или более выходах есть признак принадлежности к классу, считается, что сеть «не уверена» в своём ответе.
|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 413; Нарушение авторских прав?; Мы поможем в написании вашей работы!