Лист 4. Пересечение плоскостей

Согласно варианту построить:

- проекции двух треугольников;

- определить видимость сторон;

- линию пересечения треугольников;

- натуральную величину одного из треугольников.

На чертеже Пересечение плоскостей студент учится графическому решению позиционных задач. Под позиционными понимаются задачи, решение которых позволяет получить ответ о принадлежности элемента (точки) или подмножества (линии) множеству (поверхности). К позиционным относят также задачи на определение общих элементов, принадлежащих различным геометрическим фигурам. Данные для позиционной задачи представлены в таблице 5.

Линию пересечения заданных плоскостей можно найти:

- используя вспомогательные секущие плоскости;

- дважды применив решение задачи на пересечение прямой с плоскостью;

- применив способ замены плоскостей проекции, введя новую плоскость проекций, перпендикулярную к одной из заданных плоскостей.

Первый вариант решения обычно применяется тогда, когда проекции прямых, задающих плоскости на чертеже, не пересекаются. При этом используются плоскости уровня.

Третий вариант в ряде случаев увеличивает число графических построений на чертеже.

Решение необходимо выполнить по второму варианту. Для построения линии пересечения двух плоскостей необходимо найти какие-либо две точки, каждая из которых принадлежит обеим плоскостям. Эти точки определяют линию пересечения плоскостей.

Пример выполнения листа Пересечение плоскостей представлен на рисунке А.3.

Алгоритм решения:

1. Методом конкурирующих точек определить две стороны, участвующие в пересечении. На рисунке А.3 такими сторонами являются АВ и KD. Далее найти точку пересечения стороны АВ с плоскостью треугольника DEK.

2. Сторону АВ заключить во вспомогательную горизонтально-проецирующую плоскость 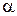. Через фронтальную проекцию стороны А^// В^// провести фронтальный след фронтально проецирующей плоскости 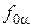, тогда .

3. Найти линию пересечения плоскостей 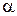и D DEK. Горизонтальный след плоскости 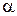пересекает проекцию плоскости D D ^/ E ^/ K ^/ в точках 2^/ и 6 ^/. 2^//–6 ^// - фронтальная проекция линии пересечения плоскостей 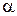и D DEK (так какфронтальный след 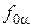фронтально проецирующей плоскости 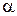обладает собирательным свойством). Для нахождения горизонтальной проекции линии пересечения данных плоскостей (2^/–6 ^/) необходимо из фронтальной проекции точек 2^// и 6 ^//провести линии связи до пересечения с горизонтальными проекциями сторон D ^/E ^/ и K ^/E ^/ соответственно.

4. Прямые AB и 2–6 лежат в одной вспомогательной плоскости 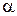и не параллельны. Горизонтальная проекция линии пересечения плоскостей 2^/–6 ^/пересекает горизонтальную проекцию А ^/ В ^/ в точке N ^/, которая и является горизонтальной проекцией точки пересечения стороны AB с плоскостью D DEK. С помощью линии связи найти фронтальную проекцию N ^//.

5. Аналогично, используя горизонтально проецирующую плоскость , определить точку пересечения стороны KD с плоскостью треугольника ABC (точка М).

6. Соединив одноимённые проекции точек M и N, определить горизонтальную (M ^/N ^/)и фронтальную (M ^//N ^//)проекции линии пересечения треугольников.

7. Видимость сторон треугольников определить способом конкурирующих точек. Видимые отрезки сторон треугольников выделить сплошными контурными линиями, невидимые следует показать штриховыми и тонкими линиями.

Натуральную величину треугольника АВС можно найти:

- методом прямоугольного треугольника;

- способом замены плоскостей;

- способами плоскопараллельного перемещения.

Определение натуральной величины необходимо выполнить по первому варианту. Для этого следует методом прямоугольного треугольника последовательно определить натуральную величину каждой стороны треугольника АВС. Зная натуральную величину сторон А^/В ₀, В^/С ₀, С^/А ₀, на свободном поле листа можно построить натуральную величину треугольника АВС.

Таблица 5

Дата добавления: 2015-06-30