Геометрические характеристики сечения

Физическая и математическая модель

Физическая модель – упрощенное представление объекта или явления, сохраняющая основные его черты. Применительно к расчетам на прочность и жесткость физическая модель должна отражать: геометрические свойства детали, свойства материала детали, действующие на деталь нагрузки.

По геометрическим признакам все тела делятся на три группы:

1. стержни – тела, у которых одно измерение существенно больше двух других (характеризуются поперечным сечением и формой оси).

2. пластины и оболочки – тела, у которых одно измерение существенно меньше двух других (характеризуются толщиной и формой серединной поверхности).

3. массивы – тела, у которых все три измерения соизмеримы.

Реальные конструкционные материалы (стали, чугуны, цветные материалы) имеют кристаллическое строение; кристаллы малы и расположены хаотично. Сложность реального строения и возникающая трудность при математическом его описании явились причиной разработки модели твердого тела. Эта модель должна сохранить основные свойства материалов и в тоже время сделать простым их аналитическое описание. Поэтому в расчетах на прочность и жесткость принимается ряд основных гипотез и допущений:

1. сплошность – материал не имеет в своей структуре пустот.

2. однородность – одинаковые свойства материала в любой точке детали.

3. изотропность – одинаковые свойства материала в различных направлениях.

4. идеальная упругость (упругость – свойство тела восстанавливать форму и размеры после снятия нагрузки; пластичность – свойство тела получать большие остаточные деформации после снятия нагрузки).

5. отсутствие первоначальных внутренних напряжений.

6. принцип малых перемещений – перемещения конструкции малы по сравнению с размерами конструкции.

7. линейная деформируемость материала – в зоне действия упругих деформаций зависимость между силой и приращением размера линейная.

8. гипотеза плоских сечений – плоское до нагружения сечение остается плоским и после нагружения.

Все свойства физической модели, описанные уравнениями, составляют математическую модель деформированного тела. Математическая модель должна содержать три группы уравнений:

1. статические - включающие нагрузки и условия равновесия;

2. физические - отражающие связь между нагрузками и деформациями;

3. геометрические - отражающие изменение формы и размеров под нагрузкой.

Сопротивление стержня различным видам деформаций часто зависит не только от материала и размеров, но и от очертаний оси, формы поперечного сечения и их расположения относительно направления действующих нагрузок. Рассмотрим основные геометрические характеристики поперечных сечений стержня, отвлекаясь от физических свойств изучаемого объекта.

1. Площадь поперечного сечения. Данная величина может быть только положительной и имеет размерность [м²]:

F= . (1)

2. Статические моменты инерции. Данная величина может быть любого знака и имеет размерность [м³]:

S_х= 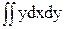, (2)

S_у= .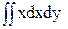

Оси, относительно которых статические моменты равны нулю, называются центральными. Точка пересечения центральных осей называется центром тяжести сечения.

3. Осевые моменты инерции. Данная величина может быть только положительной и имеет размерность [м⁴]:

I_х= 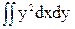, (3)

I_у= .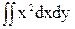

4. Центробежный момент инерции. Данная величина может быть любого знака и имеет размерность [м⁴]:

I_ху= 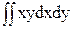. (4)

Оси, относительно которых центробежный момент равен нулю, называются главными. Главные оси, проходящие через центр тяжести, называются главными центральными осями.

5. Полярный момент инерции. Данная величина может быть только положительной и имеет размерность [м⁴]:

I_r= = = I_х+ I_у (5)

6. Осевые моменты сопротивления. Данная величина может быть только положительной и имеет размерность [м³]:

W_х= 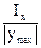, (6)

W_у= .

7. Полярный момент сопротивления. Данная величина может быть только положительной и имеет размерность [м³]:

W_r= . (7)

8. Радиусы инерции. Данная величина имеет размерность [м]:

i_x= 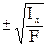, (8)

i_у= .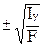

Дата добавления: 2015-06-30