Формула Пуазейля

Если бы жидкость не обладала вязкостью, то для ее течения по горизонтальной трубе не требовалось бы прилагать никакую силу. Но вследствие вязкости течение любой реальной жидкости в трубе возможно лишь тогда, когда между концами трубы создана разность давлений.

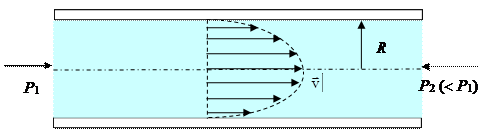
Рис.3

Рассмотрим установившееся ламинарное течение жидкости внутри цилиндрической трубы с внутренним радиусом R (рис.3). Из симметрии ясно, что в трубе частицы текущей жидкости, равноудаленные от оси, имеют одинаковую скорость. Вследствие сил сцепления между молекулами жидкости и стенками трубы скорость жидкости у стенок равна нулю. Скорость каждого следующего слоя из-за вязкого трения между ними лишь немного больше, чем скорость предыдущего слоя. Для определения зависимости скорости от расстояния, отсчитываемого от оси трубы, выделим мысленно цилиндрический объем жидкости некоторого радиуса r и длины L (рис.4). На этот цилиндр за счет разности давлений на концах трубы D P = Р ₁ – Р ₂ действует сила

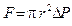, (8)

где p r ² – площадь торца цилиндра.

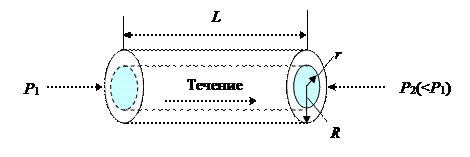
Рис.4

Движение цилиндра жидкости тормозится силой вязкого трения между ним и прилегающим к нему слоем, величина силы определяется формулой (1), где в качестве S берется площадь боковой поверхности цилиндра :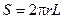

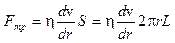, (9)

Так как жидкость движется равномерно, то силы, действующие на цилиндр взаимно компенсируются F_тр = F. Тогда с учетом (1) и (9) получим

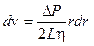(10)

Проинтегрировав это уравнение, найдем зависимость v (скорости слоев жидкости) от r (расстояния их от оси трубы), с учетом того, что v = 0 при r = R:

,

,

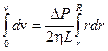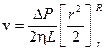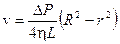. (11)

Наибольшая скорость v достигается на оси трубы (r = 0), она пропорциональна квадрату радиуса трубы, а также градиенту давления .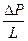

Найдем объемную скорость жидкости Q. Поскольку скорость v в поперечном сечении непостоянна, разделим (рис.5) поперечное сечение трубы на узкие кольца шириной dr, вычислим объемную скорость жидкости для каждого из этих колец и просуммируем по всем кольцам, чтобы получить объемную скорость через все сечение трубы. Площадь узкого кольца на рис.5 равна произведению длины окружности 2p r на ширину dr:

.

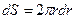Рис.5

Так как скорость жидкости v зависит только от r, в пределах одного кольца ее можно считать постоянной. Таким образом, объемная скорость жидкости, протекающей через узкое кольцо за 1 секунду, запишется в виде:

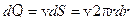(12)

Подставляя уравнение (11) в (12) получаем

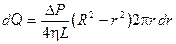. (13)

Интегрируя по всему сечению, находим объемную скорость жидкости в трубе

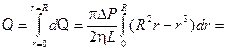
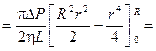
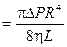или

(14)

Q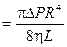

Эта зависимость известна под названием формулы Пуазейля. Решим уравнение Пуазейля относительно :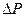

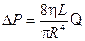(15)

и, обозначив сомножитель

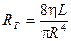, (16)

запишем

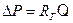. (17)

При такой записи уравнение Пуазейля сходно с законом Ома:

. (18)

Разность давлений на концах сосуда 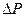аналогична напряжению U, объемная скорость кровотока Q - силе тока I, величина 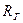, называемая гемодинамическим сопротивлением – электрическому сопротивлению R.

Аналогия, существующая между законами Ома и Пуазейля, позволяет моделировать кровообращение при помощи электрических цепей. Электрическое моделирование сердечно-сосудистой системы применяется при создании аппаратов искусственного кровообращения, в протезировании сердца и других работах.

Анализ уравнения Пуазейля, записанного в форме (15), показывает, что кровяное давление зависит от объемной скорости кровотока и, следовательно, от массы циркулирующей крови и сократительной деятельности миокарда, определяющих эту скорость. Еще более выраженное влияние на динамику кровяного давления оказывает гемодинамическое сопротивление и, прежде всего, радиус сосуда. Согласно формуле Пуазейля, объемная скорость жидкости Q пропорциональна четвертой степени радиуса трубы R, таким образом, даже небольшое изменение радиуса трубы приводит к значительному изменению Q.

Пример зависимости Q = f (R ⁴) можно найти в системе кровообращения человеческого организма. Поскольку формула Пуазейля справедлива лишь для течения несжимаемой жидкости с постоянной вязкостью h, она не может в точности выполняться для крови. Тем не менее, в этом случае формула Пуазейля является достаточно хорошим приближением. Поток крови в организме регулируется крошечными мышцами, окружающими сосуды. При сокращении этих мышц диаметр сосуда уменьшается и поток, который в соответствии с формулой (14) пропорционален R ⁴, резко сокращается уже при небольшом уменьшении радиуса. Таким образом, едва заметными сокращениями этих мышц очень точно контролируется поступление крови к различным органам. Однако, если вследствие атеросклероза (затвердевания стенок сосудов) и отложений холестерина радиус сосудов уменьшается, то для поддержания нормального кровотока требуется более высокий градиент давления. Если радиус сосудов уменьшится вдвое, то сердцу придется увеличить давление в 16 раз. В таких условиях сердце работает с перегрузкой, но, как правило, уже не может обеспечить требуемую величину потока, т.е. нормальное кровообращение.

Таким образом, повышенное артериальное давление указывает на то, что сердце работает с перегрузкой, и на то, что поток крови через артерии ниже нормы. Не случайно регуляция уровня кровяного давления в организме связана с влиянием, прежде всего, на гладко мышечную оболочку кровеносных сосудов в целях активного изменения их просвета. Сюда же направлены основные фармакологические средства нормализации кровяного давления.

Дата добавления: 2015-06-30