
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Часть 2. Аналитическая геометрия в пространстве. Часть 1. Аналитическая геометрия на плоскости
|
|
|
|
Часть 1. Аналитическая геометрия на плоскости
Бланк для ответов
Бланк для ответов
| № п/п | Суждения | Оценка в баллах | Суждения | Индекс состояния | ||||||
| Доволен | Недоволен | У | ||||||||
| Спокоен | Неспокоен | Т | ||||||||
| Напряжен | Расслаблен | Н | ||||||||
| Радостен | Огорчен | У | ||||||||
| Нужен | Лишний | Т | ||||||||
| Отдохнувший | Усталый | Н | ||||||||
| Здоровый | Больной | У | ||||||||
| Смелый | Робкий | Т | ||||||||
| Беззаботный | Озабоченный | Н | ||||||||
| Плохой | Хороший | У | ||||||||
| Ловкий | Неуклюжий | Т | ||||||||
| Свободный | Занятый | Н |
Инструкция: мысленно вернитесь в свою семью. Вспомните чувство, с которым вы открываете дверь дома. Припомните чувство, с которым вспоминаете домашние дела на работе. Как вы себя чувствуете в выходные дни и по вечерам? В общем, вспомните всю вашу семейную жизнь и ваши ощущения, связанные с семьей.
| № п/п | Суждения | Оценка в баллах | Суждения | Индекс состояния | ||||||
| Доволен | Недоволен | У | ||||||||
| Спокоен | Неспокоен | Т | ||||||||
| Напряжен | Расслаблен | Н | ||||||||
| Радостен | Огорчен | У | ||||||||
| Нужен | Лишний | Т | ||||||||
| Отдохнувший | Усталый | Н | ||||||||
| Здоровый | Больной | У | ||||||||
| Смелый | Робкий | Т | ||||||||
| Беззаботный | Озабоченный | Н | ||||||||
| Плохой | Хороший | У | ||||||||
| Ловкий | Неуклюжий | Т | ||||||||
| Свободный | Занятый | Н |
1. Заданы вершины треугольника АВС. Требуется
1) составить уравнения сторон АВС; уравнение высоты, опущенной из вершины А на сторону АС; уравнение медианы, проведенной из вершины С.
2) указать для прямой АВ координаты вектора нормали и угловой коэффициент прямой.
3) найти угол между сторонами АС и АВ, расстояние от вершины С до стороны АВ.
4) вычислить периметр треугольника АВС.
2. Построить линии. Указать элементы кривых а)-в).
3. Найти расстояние от точки  до плоскости, проходящей через три точки:
до плоскости, проходящей через три точки:  . Построить плоскость.
. Построить плоскость.
4. Написать уравнение плоскости, проходящей через точку A, перпендикулярную вектору 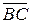 .
.
5. Найти угол между плоскостями.
6. Найти координаты точки A, равноудалённой от точек B и C.
7. Написать каноническое уравнение прямой.
8. Найти точку пересечения прямой и плоскости.
9. Нарисовать пространственные линии, заданные пересечением двух поверхностей, установив предварительно, какие это поверхности. В тех случаях, когда это необходимо, привести уравнения поверхностей к каноническому виду.
Вариант №1
1. А(2;-3), В(1;4), С(3;2).
2. а) 2x2+9y2=18; б) 2x2-9y2=18; в) 2x2=-y; г) (x+2)2-(y-3)2=18; д) 2x = 9y2
е) 2x-9y-18=0; ж)  ; з)
; з) 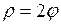
3. 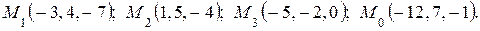
4. 
5.  ;
; 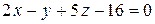 .
.
6. 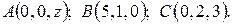
7. 
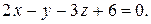
8.  ;
; 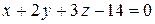 .
.
9. 
Вариант №2
1. А(6;0), В(-2;4), С(3;-4).
2.а) 3x2+8y2=24; б) 3x2-8y2=-24; в) 3x2=-y; г) (x-4)2+(y+1)2=24; д) 3x =8y2;
е) 3x+8y-24=0; ж)  ; з)
; з) 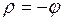
3. 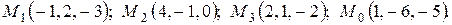
4. 
5. 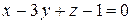 ;
;  .
.
6. 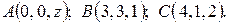
7. 

8. 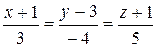 ;
;  . 9.
. 9. 
Вариант №3
1. А(0;2), В(1;3), С(-6;-4)
2. а) 5x2+9y2=45; б) 5x2-9y2=-45; в) 5x2=-9y; г) (x-5)2+(y+2)2=45; д) 5x =- 9y2
е) 5x+9y+45=0; ж)  ; з)
; з) 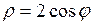
3. 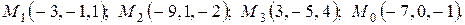
4. 
5.  ;
; 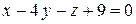 .
.
6. 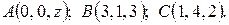
7. 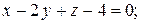
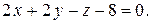
8.  ;
;  . 9.
. 9. 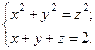
Вариант№4
1. А(3;2), В(-1;4), С(5;7).
2. а) 4x2+7y2=28; б) 4x2-7y2=28; в) 4x2=7y; г) (x-4)2+(y+3)2=28; д) 4x =-7y2
е) 7у-4х=28; ж)  ; з)
; з) 
3. 
4. 
5. 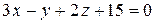 ;
; 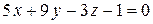 .
.
6. 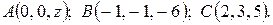
7. 

8. 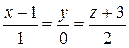 ;
; 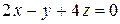 . 9.
. 9. 
Вариант №5
1. A(-1;3), B(2;4), C(1;-5),
2.а) 2x2+7y2=42; б) 2x2-7y2=42; в) 2x2=7y; г) (x+1)2+(y-7)2=21; д) 2x =-7y2
е) 2х-7у+42=0; ж)  ; з)
; з) 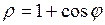
3. 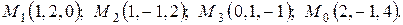
4. 
5.  ;
;  .
.
6. 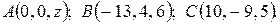
7. 

8.  ;
; 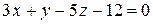 . 9.
. 9. 
Вариант №6
1. А(-2;0), В(2;6) и С(4;2),
2. а) 5x2+8y2=80; б) 5x2-8y2=80; в) 5x=-y2; г) (x-5)2+(y+3)2=10; д) x2 =-8у
е) 5х-8у-40=0; ж) 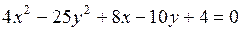 ; з)
; з) 
3. 
4. 
5.  ;
;  .
.
6. 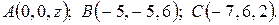
7. 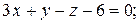
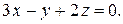
8.  ;
;  . 9.
. 9. 
Вариант №7
1. А(2;-3), В(4;5), С(-1;6).
2. а) 4x2+9y2=36; б) 4x2-9y2=-36; в) 4x2=9y; г) (x-1)2+(y+2)2=8; д) 4x = -y2
е) 3x+2y-6=0; ж) 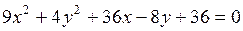 ; з)
; з) 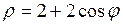
3. 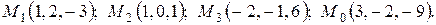
4. 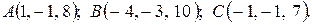
5. 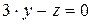 ;
;  .
.
6. 
7. 
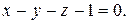
8. 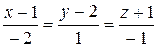 ;
;  . 9.
. 9. 
Вариант №8
1. А(-2;0), В(2;4), С(4;0).
2. а) 2x2+9y2=18; б) 2x2-9y2=18; в) 2x2=-y; г) (x-2)2+(y-1)2=18; д) x = 9y2
е) 2x+9y-18=0; ж)  ; з)
; з) 
3. 
4. 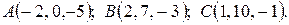
5. 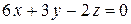 ;
; 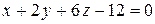 .
.
6. 
7. 
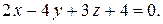
8. 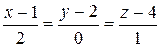 ;
; 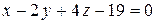 . 9.
. 9. 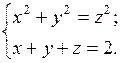
Вариант №9
1. A(0;2), B(1;-1), C(3;-2),
2.а) x2+4y2=20; б) x2-4y2=-20; в) x2=-4y; г) (x-1)2+(y+2)2=20; д) x =4y2
е) х-4у+20=0; ж)  ; з)
; з) 
3. 
4. 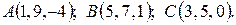
5. 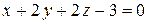 ;
; 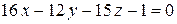 .
.
6. 
7. 

8. 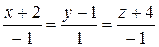 ;
; 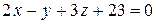 . 9.
. 9. 
Вариант №10
1. A(-1;3), B(4;0), C(5;5),
2. а) 6x2+11y2=66; б) 6x2-11y2=-66; в) 6x2=y; г) (x+6)2+(y-3)2=11; д) x =3y2
е) 6х+3у=-12; ж)  ; з)
; з) 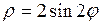
3. 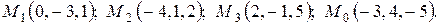
4. 
5. 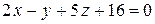 ;
;  .
.
6. 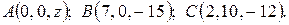
7. 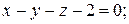

8.  ;
; 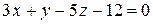 . 9.
. 9. 
Вариант №11
1. А(2;-3), В(1;4), С(3;2).
2. а) 2x2+9y2=18; б) 2x2-9y2=18; в) 2x2=-y; г) (x+2)2-(y-3)2=18; д) 2x = 9y2
е) 2x-9y-18=0; ж)  ; з)
; з) 
3. 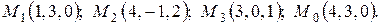
4. 
5.  ;
;  .
.
6. 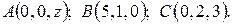
7. 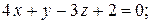

8.  ;
;  . 9.
. 9. 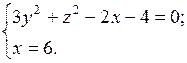
Вариант №12
1. А(6;0), В(-2;4), С(3;-4).
2. а) 3x2+8y2=24; б) 3x2-8y2=-24; в) 3x2=-y; г) (x-4)2+(y+1)2=24; д) 3x =8y2
е) 3x+8y-24=0; ж) 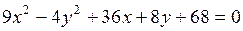 ; з)
; з) 
3. 
4. 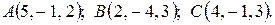
5. 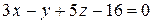 ;
;  .
.
6. 
7. 
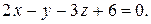
8.  ;
;  . 9.
. 9. 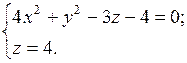
Вариант №13
1. А(0;2), В(1;3), С(-6;-4),
2. а) 5x2+9y2=45; б) 5x2-9y2=-45; в) 5x2=-9y; г) (x-5)2+(y+2)2=45; д) 5x =- 9y2
е) 5x+9y+45=0; ж) 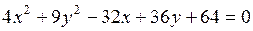 ; з)
; з) 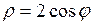
3. 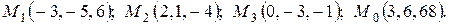
4. 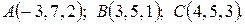
5.  ;
;  .
.
6. 
7. 
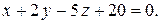
8. 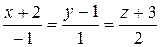 ;
;  . 9.
. 9. 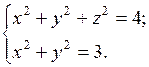
Вариант №14
1. А(3;2), В(-1;4), С(5;7).
2. а) 4x2+7y2=28; б) 4x2-7y2=28; в) 4x2=7y; г) (x-4)2+(y+3)2=28; д) 4x =-7y2
е) 7у-4х=28; ж)  ; з)
; з) 
3. 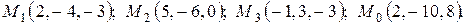
4. 
5.  ;
;  .
.
6. 
7. 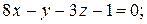

8.  ;
;  . 9.
. 9. 
Вариант №15
1. A(-1;3), B(2;4), C(1;-5),
2. а) 2x2+7y2=42; б) 2x2-7y2=42; в) 2x2=7y; г) (x+1)2+(y-7)2=21; д) 2x =-7y2
е) 2х-7у+42=0; ж) 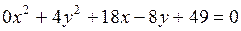 ; з)
; з) 
3. 
4. 
5. 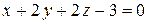 ;
;  .
.
6. 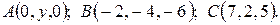
7. 

8. 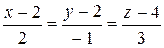 ;
; 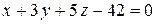 . 9.
. 9. 
8.  ;
;  . 9.
. 9. 
|
|
|
|
|
Дата добавления: 2015-06-30; Просмотров: 358; Нарушение авторских прав?; Мы поможем в написании вашей работы!