Тыс.руб

И т.д.

,.

2) Найдём размах вариации:

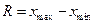= 4,29 – 3,70 = 0,59

R = 0,59.

3) Найдем ширину интервала:

.

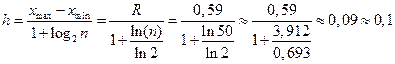h = 0,1

4) Установим полную шкалу интервалов (а₁ – в₁ ], (а₂ – в₂ ] и т.д.:

,

,

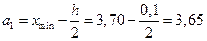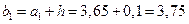Группируем результаты наблюдений по интервалам, подсчитываем накопление частот и заполняем таблицу 1.

Таблица 1

Интервалы (ai – bi]	Подсчёт частот	Частоты (ni)	Накопленные частоты ni^нак
(3,65-3,75]	/
(3,75-3,85]	//////
(3,85-3,95]	///////////
(3,95-4,05]	///////////////
(4,05-4,15]	/////////
(4,15-4,25]	//////
4,25-4,35]	//
		∑ = 50	-

II. Изобразим гистограмму, полигон и кумуляту распределения:

При построении гистограммы на оси абсцисс откладываем интервалы, а на оси ординат – частоты. Получаем ступенчатую фигуру из прямоугольников.

При изображении интервального вариационного ряда в виде полигона предполагается, что в пределах интервалов частоты распределяются равномерно. Практически это означает, что соединив середины верхних оснований прямоугольников отрезками прямой, получим полигон того же распределения.

Полигон и гистограмма частот

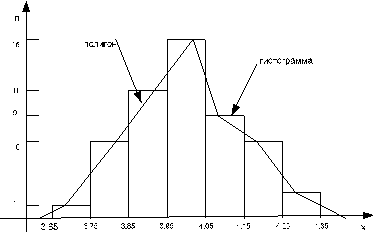
Рис.1.

Кумулята

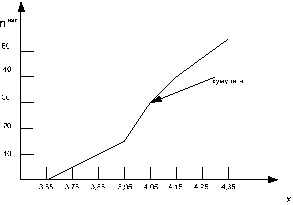
III. Выполним расчет статистических характеристик исследуемого вариационного ряда и заполним таблицу 2.

Таблица 2

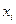
Интервалы (ai – bi]	Частоты	Центры интервалов	Расчётные графы
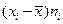
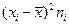
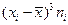
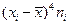
(3,65-3,75]		3,7	3,7	-0,302	0,0912	-0,0275	0,0083
(3,75-3,85]		3,8	22,8	-1,212	0,2448	-0,0494	0,0100
(3,85-3,95]		3,9	42,9	-1,122	0,1144	-0,0117	0,0012
(3,95-4,05]		4,0	60,0	-0,030
(4,05-4,15]		4,1	36,9	0,882	0,0864	0,0085	0,0008
(4,15-4,25]		4,2	25,2	1,188	0,2352	0,0466	0,0092
(4,25-4,35]		4,3	8,6	0,596	0,1776	0,0529	0,0158
∑		-	200,1		0,9496	0,0194	0,0453

1) Вычислим среднюю производительность труда (выборочную среднюю вариационного ряда)

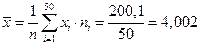(тыс. руб.).

Правильность вычисления выборочной средней можно проверить равенством

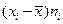∑ = 0 (смотри 6 столбец таблицы 2).

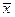= 4,002 тыс.руб.

2) Вычислим выборочную дисперсию (используем результаты 7столбца таблицы 2).

Дисперсия (рассеяние) характеризует разброс случайной величины Х относительно математического ожидания (среднего значения случайной величины).

(тыс. руб.),

где 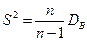– несмещенная оценка дисперсии, используемая в решении практических задач при n ≥ 30.

S² = 0,01899 тыс.руб.

3) Вычислим среднее квадратическое отклонение.

Дисперсия имеет размерностьквадрата с.в. Х, что в сравнительных целях неудобно. Поэтому, чтобы оценка разброса имела размерность случайной величины Х, используют среднее квадратичное отклонение.

S = (тыс. руб.).

Проверим соотношение R > S: в нашем случае 0,59 > 0,138 соотношение выполняется.

S = 0,138 тыс.руб.

4) Определим коэффициент асимметрии вариационного ряда.

Если полигон скошен (т.е. одна из ветвей, начиная от вершины, длиннее ругой), то ряд асимметричный (при А>0 – правосторонняя асимметрия, при А<0 – левосторонняя асимметрия).

,

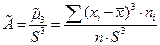где 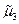- центральный момент 3-го порядка (смотри 8 столбец таблицы 2).

.

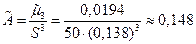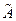= 0,148.

ВЫВОД. Т.к. 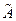> 0, то имеем правостороннюю асимметрию (слева от вершины ветвь более короткая, т. е. в вариационном ряде преобладают варианты по значению больше ).

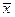5) Найдем эксцесс вариационного ряда.

Эксцесс является показателем «крутости» вариационного ряда по сравнению с нормальным законом распределения. Эксцесс нормально распределенной величины равен нулю.

Если Е > 0 (E < 0), то полигон вариационного ряда имеет более крутую (пологую) вершину по сравнению с нормальной кривой.

.

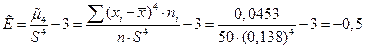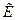= - 0,5

ВЫВОД. Т.к. 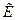< 0, то данное распределение плосковершинное, т.е. кривая по сравнению с нормальной кривой является менее крутой.

6) Найдем медиану.

Медиана - порядковая величина, характеризующая среднее значение признака, вокруг которого концентрируются наблюдения.

Достоинство медианы как меры центральной тенденции заключается в том, что на её не влияет изменение крайних членов вариационного ряда. Медиана предпочтительнее для ряда, у которого крайние варианты по сравнению с остальными оказались чрезмерно большими или малыми.

Определим полусумму частот: .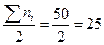

Число 25 принадлежит интервалу (3,95 – 4,05], следовательно – это медианный интервал.

, ,

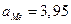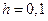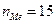(частота медианного интервала),

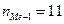(частота интервала, предшествующего медианному).

Находим медиану: 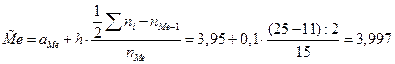(тыс.руб.).

7) Определим моду.

Мода - порядковая величина, характеризующая среднее значение признака, вокруг которого концентрируются наблюдения. Особенность моды как меры центральной тенденции заключается в том, что она не изменяется при изменении крайних членов ряда, т. е. обладает определенной устойчивостью к вариации признака.

Найдем модальный интервал (3,95 – 4,05], т.к. ему соответствует наибольшая частота n_i = 15.

Определим моду: 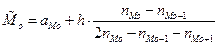, где

- начало модального интервала,

h - ширина интервала,

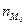- частота модального интервала,

- частота предшествующего интервала,

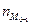- частота последующего интервала.

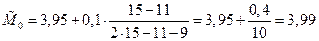(тыс.руб.).

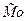= 3,99 тыс. руб. (отметим моду на рис.1).

8) Вычислим средние ошибки (Δ) асимметрии и эксцесса:

; ; ; .

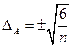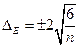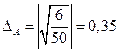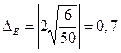Наличие асимметрии и эксцесса считается существенным, если абсолютная величина каждого из них превышает абсолютную величину своей ошибки, по крайней мере, в три раза:

; ; ; .

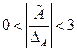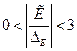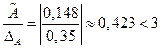Т.о. с полной достоверностью (γ = 0,95) наблюдаемые правостороннюю асимметрию и плосковершинность распределения можно считать статистически несущественным, т.е. сдвиг вершины распределения вправо и вниз произошел под воздействием случайных факторов.

IV. Выполним оценку степени близости эмпирического распределения одному из теоретических законов распределения.

Одной из задач математической статистики является установление теоретического закона распределения случайной величины, характеризующей изучаемый признак по опытному (эмпирическому) распределению, представляющему вариационный ряд.

Предположение о виде закона распределения может быть выдвинуто, исходя из теоретических предпосылок. При обработке экономических данных в качестве теоретического распределения чаще всего используется нормальный закон распределения. Проверка гипотезы о том, что эмпирическое (опытное) распределение подчиняется нормальному закону, может быть выполнена, используя χ² - критерий Пирсона.

Схема применения критерия χ²

для проверки гипотезы Н (о нормальном законе распределения случайной величины)

1. Определяется мера расхождения эмпирических (χ²_н) и теоретических (χ²_α,k) частот:

χ²_α,k – определяется по таблице «Критические точки распределения χ²»

(Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике [Учебное пособие] /В.Е. Гмурман// М.: Высшее образование. – 2007. – с. 393, приложение 5)

по уровню значимости α и числу степеней свободы k,

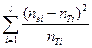χ²_н – определяется по формуле χ²_н = , где

χ²_н - наблюдаемое значение критерия,

n_{э i} - эмпирическая частота i -го интервала,

n_Ti - теоретическая частота i -го интервала,

l - число интервалов.

2. Для выбранного уровня значимости α = 1 – γ = 1 – 0,95 = 0,05,

где γ = 0,95 – доверительная вероятность или надежность оценки,

при числе степеней свободы k = m – r – 1, где

m – число интервалов(объединенных) эмпирического распределения,

r – число параметров теоретического распределения (для нормального распределения r = 2, т.е. х_в – средняя выборочная и Ϭ – среднее квадратическое отклонение),

по таблице (приложение 5) находим критическое значение χ²_α,k .

3. Если χ²_н ≤ χ²_α,k, то гипотеза Н не противоречит опытным данным,

если χ²_н > χ²_α,k, то гипотеза Н отвергается.

Применение критерия χ² требует выполнение следующих условий:

а) объем выборки должен быть достаточно высок (n ≥ 50);

б) сумма эмпирических частот должна быть равна сумме теоретических частот;

в) интервалы должны быть заполнены (т.е. в каждом интервале должно быть не менее 5 – 10 наблюдений).

Проверим выполнение условий:

а) n = 50,

б) для проверки второго условия построим таблицу 3.

Вероятность попадания случайной величины Х в интервал (a_i – b_i) вычисляем по интегральной теореме Лапласа: p_i = P(a_i ≤ x ≤ b_i) = Φ(t_bi) - Φ(t_ai),

;

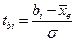(значение функции Лапласа смотри: Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике [Учебное пособие] /В.Е. Гмурман// М.: Высшее образование. – 2007. – с. 390, приложение 2).

Таблица 3

Интервалы	пэi	tai	tbi	Φ(tai)	Φ(tbi)	pi	npi	nTi
1	2	3	4	5	6	7	8	9
(3,65-3,75]		- 2,55	- 1,82	- 0,4946	- 0,4656	0,039	1,95
(3,75-3,85]		- 1,82	- 1,10	- 0,4656	- 0,3643	0,101	5,05
(3,85-3,95]		- 1,10	- 0,38	- 0,3643	- 0,1480	0,216	10,80
(3,95-4,05]		- 0,38	0,35	- 0,1480	0,1368	0,285	14,25
(4,05-4,15]		0,35	1,07	0,1368	0,3577	0,221	11,05
(4,15-4,25]		1,07	1,80	0,3577	0,4641	0,106	5,30
4,25-4,35]		1,80	2,52	0,4641	0,4941	0,030	1,50
∑							49,9

Для заполнения столбца 9 учитываем, что n = 50, n_Ti≈ np_i.

Для проверки третьего условия выполним расчёт наблюдаемого значения χ²_н , а выполненные вычисления поместим в таблице 4.

Т.к. в первом и последнем интервалах число наблюдений меньше пяти, то объединяем первые два интервала и последние два интервала, для того чтобы число вариант в полученных интервалах было больше пяти.

Таким образом число интервалов становится l = 5.

Таблица 4

Интервалы	пэi	nTi	пэi – nTi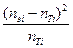
(3,65-3,75]
(3,75-3,85]
(3,85-3,95]
(3,95-4,05]				0,0714
(4,05-4,15]				0,3636
(4,15-4,25]				0,1429
4,25-4,35]
∑				χ^2н = 0,5779

По таблице «Критические точки распределения χ²» (приложение 5) при уровне значимости α = 0,05 и числом степеней свободы k = m – r – 1 = 5 – 2 – 1 = 2 находим значение критерия согласия χ²_α,k = 6.

При проверке χ²_н ≤ χ²_α,k, имеем 0,5779 < 6.

ВЫВОД: Т.к. χ²_н < χ²_α,k гипотеза о случайном расхождении эмпирического (экспериментального) и теоретического распределений не отвергается, другими словами: эмпирическое (опытное) распределение подчиняется нормальному закону распределения.

Т.е. производительность труда для данной совокупности предприятий подчиняется нормальному закону.

Можно сказать, что колебания уровней производительности труда на предприятиях отрасли объясняются в основном случайными причинами.

Дата добавления: 2015-07-01