Тема : трапеция

Тема: квадрат.

1.Определение: прямоугольник, у которого все стороны равны.

2.Свойства квадрата: т.к. квадрат является параллелограммом, прямоугольником, ромбом,

то он обладает всеми их свойствами.

3. Площадь: S = a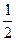² = d²

4. Замечание: в квадрат можно вписать окружность (r = 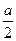), около квадрата можно описать окружность (R = = ).

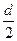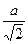1.Определение: четырехугольник, у которого только две стороны параллельны. Параллельные

стороны называют основаниями, непараллельные – боковыми.

2.Виды трапеции: прямоугольная и равнобедренная(равнобокая).

3.Определение: отрезок, соединяющий середины боковых сторон трапеции называют

средней линией трапеции.

4.В равнобокой трапеции проекция диагонали на большее основание равна средней линии.

5. Теорема: средняя линия трапеции параллельна основаниям и равна их полусумме.

6.Площадь трапеции:

• S = 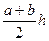(a и b – основания)
• S = 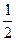d₁ d₂ sinγ (γ – угол между диагоналями)

7.Замечание: описать окружность можно только около равнобокой трапеции, вписать

окружность можно только в трапецию, у которой суммы противолежащих сторон равны,

т.е. a + c = b + d

8.Теорема: если диагонали равнобокой трапеции перпендикулярны, то её площадь можно вычислить по формуле S = h².

9.Теорема: высота равнобокой трапеции, в которую можно вписать окружность, является средним геометрическим её оснований: h = .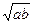

10.Теорема: длина отрезка, соединяющего середины диагоналей любой трапеции равна

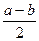(a и b –основания).

11.Теорема: длина отрезка, параллельного основаниям трапеции и делящего его на две

равновеликие вычисляется по формуле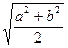

12.Дополнительные построения при решении задач, связанных с трапецией:

• Бывает полезно провести через одну из её вершин прямую, параллельную противоположной боковой стороне
• Если в условии говорится о диагоналях, то часто стоит провести через вершину прямую, параллельную диагонали
• Бывает полезно опустить перпендикуляры из вершин верхнего основания на нижнее (провести высоты)
• Можно продлить боковые стороны до пересечения и рассмотреть полученный треугольник

Дата добавления: 2015-06-27