Определительные испытания

Эти испытания проводятся для определения реального уровня надежности электрических машин. Испытаниям подвергается выборка из генеральной совокупности. Ис-

черпывающей характеристикой надежности технических изделий является закон распределения вероятности безотказной работы, по которому можно легко определить любую интересующую нас характеристику надежности.

По результатам испытаний могут быть получены точечные оценки параметра и интервальные оценки. При интервальных оценках определяется, какой интервал с заданной доверительной вероятностью Р накрывает математическое ожидание оцениваемого параметра А. Границы такого интервала носят название доверительных границ:

Р = Р(А_п <А< А_в),

где А_н, А_в — нижняя и верхняя доверительные границы параметра А.

Вероятность того, что значение А выйдет из интервала А_и, А_в, называют уровнем значимости а. В технике наиболее часто употребляемые значения доверительных вероятностей равны 0,9; 0,95; 0,99, что соответствует уровням значимости 0,10; 0,05; 0,01 соответственно.

Полученные по отказам изделий данные подвергаются статистической обработке, в результате которой решаются следующие задачи:

1) определение вида функции плотности распределения или интегральной функции распределения;

2) вычисление параметров полученного распределения;

3) установление с помощью критериев согласия степени совпадения экспериментального распределения с теоретическим;

4) определение параметров надежности исследуемых изделий.

Наиболее известными и распространенными теоретическими распределениями являются: экспоненциальное, нормальное, логарифмически нормальное, распределение Вейбулла и гамма-распределение. Поэтому при определении вида распределения аппроксимируют экспериментально полученные характеристики этими законами и выбирают из них наиболее совпадающий с экспериментальным.

Для выбора вида теоретического распределения, совпадающего в наибольшей мере с экспериментальным, чаще всего применяются метод максимума правдоподобия и метод наименьших квадратов (для определения параметров распределения при полных выборках). Для оценки степени совпадения эмпирической и теоретической зависимостей применяются критерии согласия, обычно критерий Пирсона (к²) или критерий Колмо-

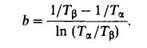
горова. Методика применения этих критериев приводится в [1].

При графическом методе оценки закона распределения на бумагу со специальной координатной сеткой наносят значения Hiftji, или (1-Я,/2>₍), где Н₍-накопленное к данному моменту времени число отказов; £п; — общее число отказов.

При проверке экспоненциального закона используется бумага с равномерной шкалой по оси времени t (по оси обсцисс) и логарифмической шкалой по оси ординат. При проверке нормального закона шкала по оси абсцисс остается равномерной, а по оси ординат используется шкала, соответствующая нормальному закону. При проверке логарифмически нормального закона по оси абсцисс используется логарифмическая шкала, по оси ординат — шкала, соответствующая нормальному закону. При проверке закона Вей-булла используются специальные шкалы.

После нанесения экспериментальных точек на бумагу проводится проверка, состоящая в определении возможности линейной интерполяции экспериментальных данных, определении наибольшего отклонения D и проверке по критерию согласия Колмогорова.

Прямую проводят так, чтобы отклонения экспериментальных точек от нее были минимальным, а сами точки располагались по обе стороны от прямой.

Наибольшее отклонение определяется сравнением отклонений по оси ординат экспериментальных точек от прямой при различных значениях времени. Критерий согласия Колмогорова рассчитывается по формуле D ]гп, где п — общее число экспериментальных точек. Если D J/n < 1,0, то гипотеза о предполагаемом законе распределения подтверждается, если D уп > 1,0, то гипотеза отвергается. После подтверждения вида закона распределения определяют параметры этого закона.

Дата добавления: 2015-06-27