Введение. Замкнутая электрическая цепь, состоящая из конденсатора С, соединенного последовательно с катушкой индуктивности L

Замкнутая электрическая цепь, состоящая из конденсатора С, соединенного последовательно с катушкой индуктивности L, называется колебательным контуром. Реальный колебательный контур обладает электрическим сопротивлением, которое на схеме обозначено в виде резистора R.

Рассмотрим электрическую цепь, состоящую из колебательного контура

С, L, R и источника постоянного тока, ЭДС которого e (рис. 1).

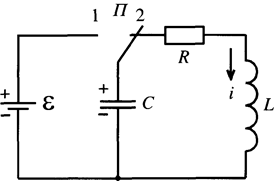
Рис. 1.

При помощи переключателя П подключим источник питания к конденсатору (переключатель П в положении 1) и зарядим его. Конденсатор при этом запасает некоторое количество энергии. Затем переведем переключатель в положение 2. Теперь заряженный конденсатор будет входить в замкнутую цепь колебательного контура, и все процессы в контуре будут происходить без участия источника питания под влиянием электрического поля конденсатора. Напишем уравнение по второму правилу Кирхгофа для колебательного контура

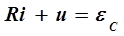, (1)

где i - ток в цепи, и - напряжение на конденсаторе, e_с - ЭДС самоиндукции катушки.

Подставим в уравнение (1) ЭДС самоиндукции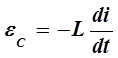

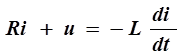-2-

. (2)

В этом выражении несколько неизвестных переменных величин: i, u, di/dt. Выразим их через одну переменную, например, через напряжение на конденсаторе и, учитывая, что

, , .

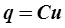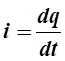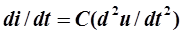Тогда уравнение (2) примет вид

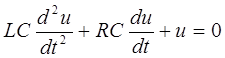, (3)

или

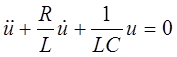. (4)

Заменим 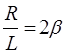, , 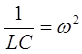и перепишем уравнение (4)

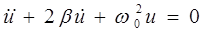, (5)

где b - коэффициент затухания, w_о - циклическая частота незатухающих колебаний в колебательном контуре.

Уравнение (5) является дифференциальным уравнением второго порядка, решая которое можно получить зависимость напряжения на конденсаторе и от времени t.

Сначала рассмотрим случай, когда сопротивление контура R = 0. Уравнение (5) в этом случае будет выглядеть так:

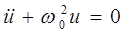. (6)

Его решением будет гармоническая функция

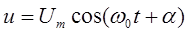. (7)

При t = 0 (момент переключения переключателя П из положения 1 в положение 2, рис. 1) напряжение на конденсаторе максимально и = U_m и ток в контуре равен нулю, i = 0. При этих начальных условиях начальная фаза a = 0 и уравнение (7) приобретает вид

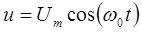.. (8)

Здесь w₀- собственная частота колебательного контура, которая определяется его параметрами L и С

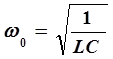. (9)

-3-

Следует отметить, что наряду с колебаниями напряжения и на конденсаторе будут изменяться с той же частотой в контуре и другие физические величины: заряд на пластинах и напряженность электрического поля в конденсаторе, ток в контуре и магнитная индукция в катушке.

Если активное сопротивление контура R не велико, так что b ² << w²₀, то уравнение (5) имеет следующее решение:

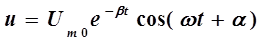, (10)

где U_mo - напряжение на конденсаторе в начальный момент времени t = 0. В этот момент и = U_mo, следовательно, начальная фаза колебаний a = 0.

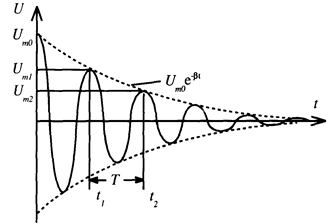
Из формулы (10) видно, что амплитуда колебаний убывает с течением времени как е^{-b t}, т. е. такие колебания называются затухающими (рис. 2).

Частота затухающих колебаний зависит от параметров колебательного контура L и С, так как w_о зависит от них, а также от коэффициента затухания b

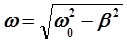. (11)

За период колебаний в этом случае можно принять величину

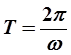
Рис.2

Для характеристики скорости затухания колебаний вводится физическая величина, называемая логарифмическим декрементом затухания, который по определению, есть логарифм отношения соседних амплитуд колебаний (см. рис. 2)

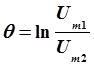. (12)

Логарифмический декремент затухания связан с коэффициентом затухания b и периодом колебаний Т следующим образом:

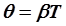. (13)

При слабом затухании w» w₀ период можно считать равным ,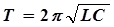

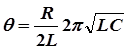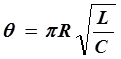; . (14)

Для характеристики колебательных свойств системы применяется величина Q, называемая добротностью контура, которая также связана с длительностью процесса затухания колебаний. Она определяется так:

-4-

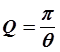. (15)

Добротность обладает простым физическим смыслом. Амплитуда напряжения на конденсаторе убывает со временем по закону е ^{-b T}. Энергия заряженного конденсатора пропорциональна квадрату амплитуды напряжения, т. е. энергия уменьшается как е^{- 2 bT}. Относительное уменьшение энергии за один период колебаний будет таким:

.

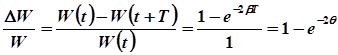При небольшом затухании логарифмический декремент затухания q < 1,

поэтому 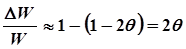, откуда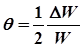

Подставив это выражение в формулу (15), получим

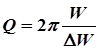(16)

Таким образом, добротность колебательного контура Q пропорциональна отношению энергии, содержащейся в контуре, к потерям энергии DW за время одного колебания (за период).

Рассмотрим случай сильного затухания, когда b = w₀. Согласно формуле (11) колебания в таких условиях становятся невозможными, так как w = 0, напряжение на конденсаторе уменьшается со временем апериодически

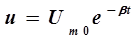. (17)

Такой процесс имеет место в том случае, если активное сопротивление контура достигает критической величины (или превышает ее). Значение критического сопротивления можно найти из условия b ² = w ².

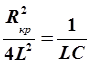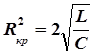, . (18)

Следует иметь в виду, что величина критического сопротивления определяется не только активным сопротивлением контура, но и другими потерями в контуре - рассеянием электромагнитного поля, потерями в диэлектрика конденсатора, потерями на перемагничивание магнетика и токами Фуко если магнитное поле катушки пронизывает соответствующие предметы, находящиеся внутри или вблизи колебательного контура.

Дата добавления: 2015-07-02