Интегрирование методом замены переменой или способом подстановки

Интегрирование по частям

Интегрирование методом замены переменой или способом подстановки

Лекция №6.

Тема: «Методы интегрирования (замена, «по частям»)».

Основные вопросы:

Пусть требуется найти интеграл , причем непосредственно подобрать первообразную для f(x) мы не сможем, но нам известно, что она существует.

Сделаем замену переменной в подынтегральном выражении, положив

x=φ(t), (1)

где φ(t)-непрерывная функция с непрерывной производной, имеющая обратную функцию. Тогда dx= φ′(t)dt;докажем, что в этом случае имеет место следующее равенство:

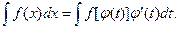(2)

Здесь подразумевается, что после интегрирования в правой части равенства вместо t будет подставлено его выражение через х на основании равенства (1).

Для того чтобы установить, что выражения, стоящие справа и слева, одинаковы в указанном выше смысле, нужно доказать, что их производные по х равны между собой. Находим производную от левой части: 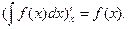Правую часть равенства (2) будем дифференцировать по х как сложную функцию, где t-промежуточный аргумент. Зависимость t от х выражается равенством (1), при этом и по правилу дифференцирования обратной функции .

Таким образом, имеем

Следовательно, производные от х от право й и левой частей равенства (2) равны, что и требовалось доказать.

Функцию следует выбирать так, чтобы можно было вычислить неопределенный интеграл, стоящий в правой части равенства (2).

Замечание. При интегрировании иногда целесообразнее подбирать замену переменной не в виде , а в виде Проиллюстрируем это на примере. Пусть нужно вычислить интеграл, имеющий вид

.

Здесь удобно положить

,

тогда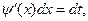

.

Приведем несколько примеров на интегрирование с помощью замены переменных.

Пример 1.

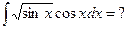Сделаем подстановку t=sin x; тогда dt= cosx dx и, следовательно,

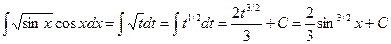
Пример 2.

Полагаем t=1+x² ;тогда dt=2xdx и

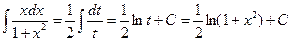
Пример 3.

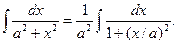Полагаем ; тогда dx=a dt,

Пример 4. 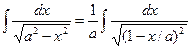. Полагаем ; тогда dx=a dt,

(предполагается, что a>0).

Пример 5. 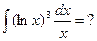Полагаем t=lnx; тогда

.

Пример 6. ? Полагаем ;тогда dt= 2xdx,

Метод замены переменных является одним из основных методов вычисления неопределенных интегралов. Даже в тех случаях, когда мы интегрируем каким -либо другим методом, нам часто приходится в промежуточных вычислениях прибегать к замене переменных. Успех интегрирования зависит в значительной степени от того, сумеем ли мы подобрать такую удачную замену переменных, которая упростила бы данный интеграл. По существу говоря изучение методов интегрирования сводится к выяснению того, какую надо сделать замену переменной при том или ином виде подынтегрального выражения. Этому посвящены большая часть настоящего пункта.

Дата добавления: 2015-07-02