Пример. Определить в множестве А элементы сравнимые с числом 6 по модулю 4, если А={3,7,9,10,12,31,29,24,20,17,1,26}

Пример

Пример

Пример

Пример

Определить в множестве А элементы сравнимые с числом 6 по модулю 4, если А={3,7,9,10,12,31,29,24,20,17,1,26}

Решение:

1. Найдем остатки от деления элементов множества А на модуль 4

3 ≡ 3 (mod 4); 7 ≡ 3 (mod 4); 9 ≡ 1 (mod 4); 10 ≡ 2 (mod 4); 12 ≡ 0 (mod 4);

31 ≡ 3 (mod 4); 29 ≡ 1 (mod 4); 24 ≡ 0 (mod 4); 20 ≡0 (mod 4); 17 ≡ 2 (mod 4);

1 ≡ 1 (mod 4); 26 ≡ 2 (mod 4)

1. Проанализируем полученные результаты и выберем те элементы множества А, которые имеют тот же остаток от деления на модуль 4, который получился в п.1.

10 ≡ 2 (mod 4); 17 ≡ 2 (mod 4); 26 ≡ 2 (mod 4)

Таким образом, получаем

6 ≡ 10 (mod 4); 6 ≡ 17 (mod 4); 6 ≡ 26 (mod 4)

Вариант	Множество	Число	Модуль
	А={3,7,9,11,12,31,29,24,20,17,6}
	С={3,17,9,18,12,31,29,25,20,39,6}
	В={13,7,4,11,20,31,26,60,78,56,22}
	А={23,17,9,21,32,11,29,24,30,47,16}
	М={3,5,6,14,27,31,29,41,20,55,44}
	D={13,25,36,24,17,1,28,31,23,54,50}
	С={43,7,19,29,12,34,29,25,20,39,6}
	К={24,17,9,30,12,31,28,25,34,39,6}
	С={3,17,9,18,12,31,29,25,20,38,73}
	Р={4,27,18,10,62,51,29,74,29,87,26}
	М={17,7,36,14,27,37,29,49,20,53,41}
	А={23,7,9,11,14,31,29,84,20,17,16}
	С={3,11,89,18,12,31,29,25,20,39,6}
	В={33,59,4,11,20,31,26,60,75,56,22}
	А={23,47,50,21,32,15,29,24,30,47,16}
	М={64,5,16,44,27,31,29,41,20,56,44}
	D={13,26,36,27,38,2,28,31,23,54,61}
	С={43,7,26,129,14,31,29,46,20,39,66}
	К={24,14,194,37,12,131,33,25,95,39,4}
	С={3,17,9,18,12,31,30,25,90,38,72}
	Р={4,27,19,10,62,53,29,74,29,87,26}
	А={3,67,99,11,62,31,29,55,20,17,46}
	С={43,17,79,46,12,31,29,125,20,39,16}
	В={33,7,44,11,26,31,126,80,68,54,22}
	А={23,17,309,121,32,114,29,24,147,42,16}
	М={17,5,46,14,27,31,29,42,21,58,47}
	D={13,26,39,24,127,1,27,131,23,54,50}
	С={43,7,119,25,12,34,129,25,95,39,26}
	К={24,17,58,30,13,31,28,25,135,29,97}
	С={13,114,19,78,12,44,29,125,20,38,73}

Задание 4. Определить функцию Эйлера для числа m.

m = 24

Решение.

Если число m простое то .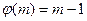

Если число m имеет каноническое разложение

m = p …p ,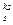

то

1 Найдем каноническое разложение числа

m = 24 = 2³*3

2 Найдем функцию Эйлера, используя приведенную формулу.

.

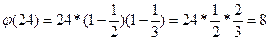Таким образом, функцию Эйлера для числа m = 24 равна .

Вариант

m

Вариант

m

Задание 5. Найти остаток от деления числа a на число b.

a = 13¹⁶²; m = 17

Решение.

1. Найдем НОД чисел a = 13 и m = 17.

d = (a, m) = (13, 17) = 1,

таким образом, числа 13 и 17 взаимно простые.

1. Так как (13,17) = 1 и 17 простое число, то 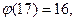применяя теорему Эйлера, получим

13¹⁶ ≡ 1 (mod 17).

Отсюда следует, что

13¹⁶² ≡ (13¹⁶)¹⁰ 13² ≡ 13² ≡ (-4)² ≡ 16 (mod 17).

Искомый остаток равен 16.

Вариант

a

7^130

13^146

5^147

11^132

13^134

7^218

11^252

5^281

13^173

13^196

7^188

5^237

17^145

17^145

15^132

m

Вариант

a

17^114

11^245

7^194

5^145

19^127

17^244

13^149

17^215

11^198

19^152

7^251

7^235

15^159

15^145

16^145

m

Задание 6. Определить принадлежат ли следующие числа заданного множества полной системе вычетов по модулю m.

А = {0,13,25,37,49,61,73}; m = 7

Решение.

Воспользуемся определением: Совокупность чисел, взятых по одному из каждого класса вычетов по модулю m, называется полной системой вычетов по модулю m.

1. Найдем остатки от деления элементов множества А на модуль 7

3 ≡ 3 (mod 7); 13 ≡ 6 (mod 7); 25 ≡ 4 (mod 7); 37 ≡2 (mod 7); 49 ≡ 0 (mod 7);

61 ≡ 5 (mod 7); 73 ≡ 1 (mod 4)

1. Проанализируем полученные результаты: так как в множестве А присутствует совокупность чисел, взятых по одному из каждого класса вычетов по модулю m (все остатки разные от 0 до 6), то данные числа принадлежат полной системе вычетов по модулю 7.

Вари- ант	Множество	Мо-дуль	Вари- ант	Множество	Мо-дуль
	А={3,11,24,20,17}			А={3,11,24,20,17}
	С={14,9,18,31,29,34}			С={17,9,18,31,56,34}
	В={13,7,11,20,26,72,57,22}			В={13,7,65,44,28,31,26,60,80,56,30}
	А={26,34,21,32,29,24,30}			А={23,17,9,22,46,61,29,24,30}
	М={3,14,27,31,29,42,19,53,34}			М={46,6,14,27,31,29}
	D={12,23,37,27,16,2}			D={56,34,59,27,24,17,1,28,31,21,54,50}
	С={43,7,19,30,34,45,18}			С={43,7,32,46,12,34,29,25}
	К={24,19,9,30}			К={24,16,9,30,22,84,57,25,34,39,4}
	С={31,29,26,21,36,82}			С={16,9,56,12,31,29}
	Р={88,18,10,62,51,29,75,32,22}			Р={34,10,67,51,23,72,39,84,26}
	М={29,50,22,51,43}			М={125,91,56,74}
	А={23,37,32,11,14,31,28,82,24,18,19}			А={23,7,9,27,14,34,42,84,20,17,16,3}
	С={8,3,15,89,18,12,32,45,6}			С={52,27,91,18,12,30,29}
	В={20,31,23,60,75,56,22}			В={33,59,4,12,28,31,97,60,75,56}
	А={23,47,50,21,33,15,29,24,30,86,16}			А={67,47,54,21,32,16,28,24,98}

Задание 6. Решить сравнение.

729 x ≡ 33 (mod 321)

Решение.

1. Упростим сравнение, заменив в нем коэффициент 729 остатком от деления на 321. Получим сравнение

87 x ≡ 33 (mod 321).

2. Проверим условие разрешимости:

Найдем НОД 87 и 321 по алгоритму Евклида.

321 = 87*3 + 60

87 = 60*1 + 27

60 = 27*2 + 6

27 = 6*4 + 3

6 = 3*2 + 0.

Таким образом, (321, 87) = 3, кроме этого свободный член 33|3, следовательно, сравнение разрешимо и имеет 3 решения по модулю 321.

3. Воспользовавшись свойствами сравнения, исходное сравнение заменим эквивалентным

29 x ≡ 11 (mod 107),

которое имеет единственное решение по модулю 107, решим его.

Применим алгоритм Евклида к числам 107 и 29

107 = 29*3 + 20

29 = 20*1 + 9

20 = 9*2 + 2

9 = 2*4 + 1

2 = 1*2 + 0.

Получим последний неравный нулю остаток r₄ = 1 и систему неполных частных
q₁ = 3, q₂ = 1, q₃ = 2, q₄ = 4. По ним, воспользовавшись рекуррентной формулой из полного алгоритма Евклида

v_k = v_k-2 – v_k-1q_k,

найдем число v = v₄, при котором 107u + 29v = 1.

Весь процесс вычисления удобно записать в виде таблице

k
qk
vk		-3		-11

Теперь можно записать решение сравнения x = 48*11 = 528 ≡ 100(mod 107).

Или решения исходного сравнения будут равны:

x₁ ≡ 100(mod 321), x₂ ≡ 207(mod 321), x₃ ≡ 314(mod 321).

Вари- ант	Сравнение	Вари- ант	Сравнение	Вари- ант	Сравнение
	48 x ≡ 18 (mod 26)		28 x ≡ 21 (mod 35)		82 x ≡ 14 (mod 35)
	36 x ≡ 16 (mod 22)		38 x ≡ 14 (mod 22)		67 x ≡ 17 (mod 18)
	72 x ≡ 15 (mod 21)		42 x ≡ 16 (mod 28)		57 x ≡ 12 (mod 45)
	79 x ≡ 24 (mod 32)		25 x ≡ 5 (mod 15)		84 x ≡ 24 (mod 46)
	42 x ≡ 21 (mod 28)		41 x ≡ 13 (mod 25)		53 x ≡ 16 (mod 24)
	12 x ≡ 7 (mod 15)		56 x ≡ 12 (mod 18)		122 x ≡ 5 (mod 19)
	27 x ≡ 9 (mod 15)		125 x ≡ 15 (mod 45)		94 x ≡ 16 (mod 33)
	25 x ≡ 15 (mod 45)		48x ≡ 24 (mod 27)		76 x ≡ 14 (mod 16)
	57 x ≡ 19 (mod 38)		47 x ≡ 12 (mod 17)		52 x ≡ 23 (mod 29)
	14 x ≡ 12 (mod 19)		25 x ≡ 15 (mod 45)		75 x ≡ 26 (mod 55)

Дата добавления: 2015-07-02