Тема: корреляционный анализ

№6

№5

№4

№3

№2

№1

Задачи для самостоятельного решения

В задачах №1-4 по приведенным данным наблюдений найдите уравнение линии регрессии и показать на графике линию регрессии.

xi
yi	1.3	2.5	3.5	5.0	7.0

xi	5,0	5,5	6,0	6,5	7,0
yi

xi
yi	1,6	2,5	4,2	6,1	7,8	8,5

xi
yi

В зависимости от тиража стоимость изготовления одного листа печатной продукции в разных типографиях составляет:

Тираж экз.	Стоимость одного листа у. е.
Типография№1	Типография№2	Типография№3	Типография№4
	1,0	1,1	1,0	1,1
	1,0	1,0	0,9	1,9
	0,9	0,9	0,9	0,9
	0,9	0,8	0,9	0,8
	0,7	0,7	0,8	0,6

а) По полученным данным зависимости стоимости изготовления 1 листа печатной продукции S от объёма тиража T постройте корреляционную таблицу

б) Найдите условные средние значения стоимости одного места для каждог8о предлагаемого тиража продукции

в) Считая функциональную зависимость 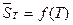линейной, определите методом наименьших квадратов значения коэффициентов k и b уравнения линейной регрессии на Т

г) Запишите уравнение линейной регрессии и постройте линию регрессии на Т

д) Используя полученное уравнение линейной регрессии, сделайте прогноз о средней стоимости одного листа печатной продукции, если тираж составит 6000экз.

Взависимости от дохода на душу населения, возраставшего в течение определенного периода, объем продаж некоторого товара в расчете на 1000жителей в разных городах менялсяследующим образом:

Доход у.е.	Количество продаж, шт.
Брест	Витебск	Гомель	Гродно	Минск	Могилев

а) По полученным данным зависимости количества продаж Q от дохода на душу населения постройте корреляционную таблицу

б) Найдите условные средние значения количества продаж для каждого размера дохода на душу населения.

в) Считая функциональную зависимость = линейной, определите методом наименьших квадратов значения коэффициентов k и b уравнения линейной регрессии

г) Запишите уравнение линейной регрессии и постройте линию регрессии на Д

д) Используя полученное уравнение линейной регрессии, сделайте прогноз о среднем количестве продаж товара, если доход на душу населения составит 110у.е..

1^o. Корреляционная зависимость двух случайных переменных величин X и Y

Корреляционный анализ – один из методов исследования статистической зависимости переменных случайных величин на основе выборочных данных.

Пусть Х – рост, Y – масса человека. Несмотря на возможные значительные различия массы человека одного и того же роста можно утверждать, что для данного роста существует некоторая средняя (оптимальная) масса. Отсюда и формулы для эталонов, т.е. рекомендации «веса» для человека определенного роста, начиная с новорожденных. Изменяется рост – изменяется и рекомендуемый средний «вес» (масса) человека. Обратно, задавая массу тела, можно указать соответствующий ей «эталонный» рост.

Данный пример иллюстрирует взаимосвязь системы двух случайных переменных величин. Однако между Х и Y может существовать только односторонняя связь: Y – степень обученности юриста-практиканта, измеряемая числом различных видов правонарушений за период его практики, Х – уровень преступности за период практики. Между Х и Y может вообще отсутствовать статистическая зависимость: Х – количество осадков, выпавших за год, Y – число абитуриентов, поступивших в СГУ за этот год. Хотя кажущаяся зависимость в определенные годы и может наблюдаться: и то и другое может расти или уменьшаться одновременно.

Если изменение одной случайной величины Х приводит к функциональному изменению среднего значения другой случайной переменной Y, т.е. если М (Y) = f (х), то связь между Х и Y называется корреляционной зависимостью. Функция f (х) называется регрессией (в вольном толковании «откликом») Y на Х. Возможна и регрессия Х на Y, т.е. М (Х) = j(y). График y = f (х) называется линией регрессии Y на Х, график x = j(y) – линией регрессии Х на Y.

Регрессия случайной зависимой переменной может иметь место и в случае, когда независимая переменная не является случайной величиной, т.е. принимает заданные значения.

2^o. Формы представления выборочных данных для корреляционного анализа

Исследование предположения о существовании корреляционной зависимости двух случайных переменных величин и формы линии регрессии обычно проводится по диаграмме рассеяния или по корреляционной таблице и называется регрессионным анализом. После проведения регрессионного анализа, для уточнения числовых параметров уравнения регрессии и выявления степени влияния изменения одной случайной переменной на другую (тесноты статистической связи случайных переменных) проводится корреляционный анализ.

Диаграмма рассеяния –

точечный график значений пар

(Х; Y) случайных величин по

данным выборки. Недостатком

диаграммы рассеяния является

отсутствие информации о час-

тоте значений (х_i, y_i). Достоинство – наглядность распределения выборочных данных. При этом форма линии регрессии y = y (x) устанавливается по точкам y_i * = , т.е. график функции y = y (x) проходит через точки (х_i, ), где – условное выборочное среднее случайной величины Y.

Корреляционная таблица –

матрица частот значений (х_i, y_i).

Достоинство – полная инфор-

мация о выборке, недостаток –

отсутствие наглядности.

3^o. Парная линейная регрессия

Рассмотрим простейшую корреляционную зависимость, при которой регрессия Y на Х – линейная функция: y = а + bx, параметр b называется коэффициентом регрессии и определяет тангенс угла наклона прямой линии регрессии относительно положительного направления оси х.

Для простоты предположим, что в выборке объемом n каждому значению х_i соответствует единственное значение, т.е. = y_i (i = ). Тогда в идеальном случае линейной регрессии прямая

y = а + bx должна пройти че-

рез все точки (х_i, y_i) диаграм-

мы рассеяния. Однако на

практике значения y_i выбор-

ки не совпадают с y (х_i) = a +

bx_i ни для каких a и b. Поэ-

тому возникает необходи-

мость найти такую прямую линию регрессии y (х) = , которая как можно близко расположится ко всем точкам выборки (х_i, y_i) одновременно, т.е. или, что равносильно, была бы минимальной, где y (х_i) – точки на прямой y (х) = , т.е. y (х_i) = , а y_i – выборочные данные для соответствующих значений х_i.

Нахождение оценок и соответствующих параметров уравнения регрессии y = а + bx путем минимизации функции F (, ) = = называется методом наименьших квадратов определения параметров эмпирической зависимости переменных.

Отметим, что этот метод не дает ответ, функция какого вида лучше отвечает исследуемой зависимости переменных (линейная, квадратичная, логарифмическая и т.д.), он позволяет лишь определить, какие параметры выбранной функции являются лучшими для полученных выборочных данных.

Выполним необходимые условия для точки экстремума F (, ) = ®min (ясно, что сверху функция F не ограничена):

Þ Þ

. Найдем , решая систему по формулам Крамера: , , следовательно, , а из второго уравнения системы: .

Аналогично находятся оценки параметров уравнения х (y) = для линейной регрессии Х на Y. Для этого в полученных выше формулах следует лишь заменить х на y, а y на х: , .

Если в уравнение регрессии Y на Х y (х) = подставить полученное выражение для = – , то это уравнение примет вид: y (х) = – . Аналогично уравнение регрессии Х на Y можно записать в виде: х (у) = – .

Если учесть, что , ,

, ,

то , .

Чтобы проверить значимость уравнения парной регрессии в целом (т.е. установить, соответствует ли линейная модель с установленными параметрами экспериментальным данным для описания зависимой переменной) используется F -критерий Фишера-Снедекора. Наблюдаемое значение критерия K _н = (n – 2)· Q_R / Q _ост, где Q_R – вариация зависимой переменной, учтенная регрессией ( = = ), Q _ост – остаточная вариация, характеризующая влияние неучтенных факторов () = ). Если K _н ³ F _a(k ₁, k ₂), где степени свободы k ₁ = 1, k ₂ = n – 2, то на уровне a полученное уравнение регрессии значимо. Отметим, что K _кр = F _a(1, n – 2) = t _g²(g, n – 1), где доверительная вероятность g = 1 – a, t _g²(g, n – 1) – квадрат соответствующего коэффициента Стьюдента.

4^o. Корреляционный анализ как один из приемов прогнозирования

Поскольку уравнение регрессии Y на Х задает зависимость статистического среднего (условного мат. ожидания) случайной переменной величины Y для каждого значения Х: = (х), то на основании уравнения регрессии с полученными оценками параметров можно получить оценку среднего для любых значений х как в пределах интервала вариант (х _min, x _max) – интерполяция, так и вне этого интервала – экстраполяция. При интерполяции значение определяется с той же погрешностью, что и само уравнение регрессии. При экстраполяции оценка может оказаться неверной, так как за пределами выборочных данных, которые были использованы при построении корреляционной модели, могут действовать иные закономерности, т.е. изменяется форма уравнения линии регрессии.

Однако это не означает, что экстраполяция вообще недопустима. Напротив, корреляционная модель, в общем случае, нацелена на обоснование прогнозируемых величин в предположении сохранения закономерностей, определяющих зависимость переменных случайных величин.

Рассмотрим приложение корреляционного анализа к прогнозированию в случае линейной зависимости случайных переменных величин, при которой существующая корреляционная зависимость y = а + bx моделируется уравнением y (х) = .

Пример: Составить прогноз товарооборота в млн. руб. на 2025 г. для фирмы по имеющимся выборочным данным (Х – годы, Y – объем товарооборота):

Х						. 2009
Y

Имеем объем выборки n = 6. Проведем расчет для независимой переменной Х, уменьшив ее значения на 1900 единиц:

= (89 + 92 + 100 + 104 + 106 + 109)/6 = 100;

= (40 + 43 + 44 + 45 + 48 +50)/6 = 45.

Найдем параметры линейного уравнения регрессии y (х) = . Для этого составим вспомогательную расчетную таблицу:

i
x –	– 11	– 8
y –	– 5	– 2	– 1
(x – )^2							å (х – )^2= 318
(x – )(y – )							å(х – )∙(y – ) = 134

1) = ×318= 53 2) = ×134 = 67/3

3) = = 0,4214 4) = 45 – 0,4214×100 = 2,86

х
y		49,2

Þ уравнение регрессии: y = 2,86 + 0,4214× x.

Строим график по двум точкам:

Делаем прогноз на 2025 год (х * = 125): y * = = 2,86 + 0,4214×125 = 55,5 млн. руб.

Рассчитаем доверительный интервал с надежностью g = 0,95: y * – d < _факт < y * + d, где d = t _g(g, n –1)×s(y *). Средняя стандартная ошибка прогнозного значения s(y *) = × , где – остаточная дисперсия случайной величины Y. Нам известны значения n = 6, х * = 125, = 100, =318. Для расчета составляем таблицу, при заполнении которой учитываем, что y (х_i)= 2,86 + 0,4214× x_i:

xi
yi
y (хi)	40,36	41,63		46,69	47,53	48,79
(y (хi)– yi)^2	0,1296	1,8769		2,8561	0,2209	1,4641	å = 7,5476

Þ s(y *) = × = 2,712. Поскольку t _g(g = 0,95, n – 1= 5) = 2,776, то d = 2,776×2,712» 7,5. Следовательно, 55,5 – 7,5 < _факт (2025) < 55,5 + 7,5. Т.о., фактическое значение в прогнозируемый 2025 год окажется с вероятностью g = 0,95 в интервале (48; 63) млн. руб. #

5^o. Уравнение множественной линейной регрессии

Рассмотрим случай множественной линейной регресии: и (x) = и (x ₁, x ₂,…, x_т) = + x ₁ + x ₂ + … + x_т, и в результате п измерений получены п значений и ^{( i )} для каждого набора значений аргументов (). В этом случае минимизируется функция F (, , …, ) = . Из условий: ¶ F /¶ = 0,…, ¶ F /¶ = 0, получаем (т + 1) уравнений:

или, полагая B = , V = , А = , получим АВ = V, откуда В = А ^–1 V.

Если построить матрицы Х = и U = ,

то Х ^Т × Х = × =

п × = п × А; Х ^Т × U = ×

= п × = п × V, следовательно, А = × Х ^Т × Х, V = × Х ^Т × U, и равенство АВ = V принимает вид × Х ^Т × Х × В = × Х ^Т × U, откуда

В = (Х ^Т × Х)^{– 1}× Х ^Т × U.

Эта формула позволяет достаточно быстро, используя, например, табличный редактор Ехсеl, получить значения числовых параметров эмпирической функции при множественной линейной регрессии. Для этого достаточно составить матрицы Х и U по результатам выполненных п измерений, т.е. по выборке объема п.

Для установления значимости на уровне a уравнения множественной линейной регрессии и (x) = + x ₁ + x ₂ + … + x_т, в котором по выборочным данным определяются m + 1 параметров, используется F -критерий Фишера-Снедекора. Наблюдаемое значение критерия K _н = (n – m – 1)· Q_R / Q _ост, где Q_R = – вариация зависимой переменной, учтенная регрессией; Q _ост = – остаточная вариация, характеризующая влияние неучтенных факторов. Если K _н ³ F _a(k ₁, k ₂), где степени свободы k ₁ = m, k ₂ = n – (m + 1), то на уровне a полученное уравнение регрессии значимо.

Дата добавления: 2015-07-02