
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Алгебра множин
|
|
|
|
Контрольні питання
1. Назвіть мету і задачі програмної інженерії.
2. Назвіть основні складові наукової дисципліни.
Множина 2U всіх підмножин універсальної множини U із заданими на ньому чотирма операціями складає алгебру множин. (cr – позначка алгебри множин)
Клас множин cr називається алгеброю (множин), якщо:
1. UÎ cr.
2. з того, що А, В Î cr виходить АÈВÎ cr.
3. з того, що А, В Î cr виходить А\ВÎ cr.
Пріоритет операцій в алгебрі множин такий:
1. доповнення  ;
;
2. перетин АÇВ;
3. поєднання АÈВ;
4. різниця А\ В
Приклад. В формулі E = A\ B È 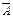 ÇB\ B можна розташувати дужки, змінюючи послідовність операцій: Р = ((A\ B) È(
ÇB\ B можна розташувати дужки, змінюючи послідовність операцій: Р = ((A\ B) È(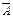 ÇB))\ B, або С = (A \ (B È
ÇB))\ B, або С = (A \ (B È 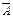 ) ÇB)\ B. В алгебрі множин cr автоматично виконуються такі тотожності, які дозволяють віднести cr до класу так званих булевих алгебр:
) ÇB)\ B. В алгебрі множин cr автоматично виконуються такі тотожності, які дозволяють віднести cr до класу так званих булевих алгебр:
| 1 Комутативний закон | |||
а) 
| б) 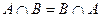
| ||
| 2 Асоціативний закон | |||
а) 
| б) 
| ||
| 3 Дистрибутивний закон | |||
а) 
| б) 
| ||
| 4 Властивості Æ і U | |||
а)  б) б) 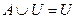
| в)  г) г) 
| ||
| 5 Закон інволюції | 6 Закон протиріччя | 7 Закон виключення | |
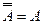
| 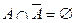
| 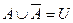
| |
| 8 Закон ідемпотентності (самопоглинання) | |||
а) 
| б) 
| ||
| 9 Закон елімінації | |||
а) 
| б) 
| ||
| 6 Закон де Моргана | |||
а) 
| б) 
| ||
Усі наведені тотожності можна наочно зобразити і довести, використовуючи діаграми Венна. Доведемо за допомогою діаграм Венна дистрибутивний закон:


Як бачимо, обидві діаграми однакові, отже тотожність справедлива.
За допомогою тотожностей алгебри множин можна здійснювати еквівалентні перетворення виразів.
Приклад. Спростити вираз: 
 = застосуємо закон де Моргана
= застосуємо закон де Моргана
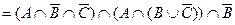 = асоціативність та комутативність
= асоціативність та комутативність
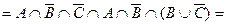 закон ідемпотентності
закон ідемпотентності
 дистрибутивний закон
дистрибутивний закон
 закони протиріччя і виключення
закони протиріччя і виключення

 Запитання
Запитання
1. Розташуйте операції алгебри множин відповідно до їх пріоритетів.
2. Назвіть тотожності алгебри множин, запишіть відповідні формули.
3. Яким чином можна графічно зобразити та довести закони і тотожності алгебри множин? Наведіть приклад такого доведення.
4. Наведіть приклад, яким чином виконуються еквівалентні перетворення формул алгебри множин.
7 Нескінченні множини
Хоча, практично обчислення чи обробка інформації завжди виконується зі скінченними множинами, але іноді неможливо вказати найбільше число n, яке не буде перевершене у всіх випадках. Тому доводиться досліджувати властивості всієї нескінченої множити чисел. Нескінченні множини можуть бути неперервними, або дискретними. Перш ніж визначати властивості нескінчених множин, розглянемо такі поняття, як відповідність.
Взаємно однозначною називається така відповідність між множинами А і В, при якій кожному елементу aÎA відповідає один і тільки один елемент bÎB, і кожному елементу bÎB відповідає один і тільки один елемент aÎA. Функція, що визначає однозначну відповідність, називається бієктивною функцією або бієкцією.
Множини А і В називають еквівалентними або рівнопотужними (А~В), якщо між ними можна встановити взаємно однозначну відповідність.
Наприклад, зал для глядачів повністю заповнений. То кількість крісел у залі дорівнює кількості глядачів. То ж множина глядачів еквівалентна множині крісел в залі. То ж для скінченних множин еквівалентними є множини з однаковою потужністю. Для нескінченної множини строге поняття потужності не вводиться, але сам термін «потужність» використовується для визначення властивості, загальної для всіх еквівалентних множин. Якщо дві нескінченні множини А і В еквівалентні (А~В), то рівність їх потужностей умовно записується як | A | = | D |.
Множина А називається зчисленною, якщо вона еквівалентна натуральному ряду N (А~N). Термін «зчисленна» є точним замінником інтуїтивного поняття «дискретна».
За допомогою бієкції j = N ® А можна «перелічити» всі елемент a з А, привласнивши їм індекси за правилом j(n) = an. Можна записати, що А = {an, n = 1, 2, …}. Множини парних натуральних чисел Nч={2, 4, 6, …}, всіх натуральних чисел N = {1, 2, 3, …}, всіх цілих Z, раціональних Q (елементи мають вигляд дробу m/n, де m,nÎZ) є послідовно вкладені Nч Ì N Ì Z Ì Q. Хоча для будь-яких двох з цих множин немає рівності, але вони еквівалентні, тобто мають однакові потужності |Nч| = |N |=| Z| = |Q|.
| m | …. | ||||||
| n | |||||||
    1/1 1/1
| 2/1 | 3/1 | 4/1 | 5/1 | … | ||
| 1/2 | 2/2 | 3/2 | 4/2 | 5/2 | … | ||
| 1/3 | 2/3 | 3/3 | 4/3 | 5/3 | … | ||
| 1/4 | 2/4 | 3/4 | 4/4 | 5/4 | … | ||
| … | … | … | … | … | … | … |
Для доведення еквівалентності множин Q і N розглянемо приведену таблицю всіх елементів множини Q, в якій також визначене правило нумерації її елементів. Тобто, кожному елементу Q можна поставити у відповідність елемент N. Таким чином множина раціональних чисел – зчисленна.
|
|
|
|
Дата добавления: 2015-07-02; Просмотров: 9184; Нарушение авторских прав?; Мы поможем в написании вашей работы!