Запитання

Булеві змінні і функції

Лекція 9

Для зображення інформації в ПК використовується двійкова система числення. Таким чином, всі операції, які використовує комп’ютер, проводяться на множині {0, 1}. Але елементарні операції з двійковими числами не схожі на елементарні арифметичні операції додавання, віднімання, тощо. Ці операції зручно зображувати за допомогою апарата двійкової логіки. Операції двійкової логіки на множині {0, 1} утворюють алгебраїчною структуру, яку називають булевою алгеброю (назва походить від прізвища англійського математика XIX століття Джорджа Буля).

Розглянемо двохелементну множину D = {0, 1}.

Змінні, які можуть приймати значення з множини В, називають логічними або булевими змінними. Самі значення 0 і 1 булевих змінних називають булевими константами.

В мовах програмування для роботи з такими змінними, як правило, вводиться спеціальний логічний тип (наприклад в мовах Turbo Pascal і Java – boolean, Si+ - Bool). Змінні такого типу можуть приймати тільки значення true і false.

Функція виду y = f (x₁, x₂,…x_n), аргументи і значеннями якої належать множині В, називається n-місною булевою функцією. Такі функції також називають логічними або перемикальними.

Кортеж (x₁, x₂,…x_n) конкретних значень булевих змінних називається двійковим словом або булевим набором довжини n. Для булевої функції y = f (x₁, x₂,…x_n) конкретне значення булевого набору (x₁, x₂,…x_n) називається також інтерпретацією булевої функції. Множина всіх двійкових слів, що позначається через Вⁿ, називається n-вимірним булевим кубом і містить 2ⁿ елементів-слів: | B | = 2ⁿ.

Для n=1 є всього 2¹=2 слова (0) і (1). Для n=2 існує 2²=4 слова (00), (01), (10), (11).

Функції кількох незалежних змінних можна розглядати як функції від більшої кількості змінних. При цьому значення функції не змінюється при зміні значення цих «додаткових» змінних.

Змінна х_і функції f(x₁, x₂, …x_i-1, x_i, x_i+1, …x_n) називається неістотною (або фіктивною), якщо f(x₁, x₂, …x_i-1, 0, x_i+1, …x_n) = f(x₁, x₂, …x_s-1, 1, x_i+1, …x_n). Якщо змінна х_і функції f(x₁, x₂, …x_i-1, x_i, x_i+1, …x_n) є неістотною, то f(x₁, x₂, …x_i-1, x_i, x_i+1, …x_n) = f(x₁, x₂, …x_i-1, x_i+1, …x_n), тобто її можна вилучити з усіх інтерпретацій і значення функції при цьому не зміниться.

Булеві функції можуть бути задані такими способами:

1. За допомогою таблиці істинності (значеннями на кожній з інтерпретацій).

2. Порядковим номером, що має ця функція;

3. Аналітично, у вигляді формули.

Розглянемо кожний з заданих способів докладніше.

1. Які змінні називають булевими або логічними змінними?

2. Дайте визначення булевої функції;

3. Що зображує область значень і область визначення булевої функції?

4. Поясніть поняття «інтерпретація булевої функції».

5.

Які змінні називають неістотними або фіктивними?

2 Таблиці істинності

Таблиці, в яких кожній інтерпретації функції (x₁, x₂,…x_n) поставлено у відповідність її значення, називаються таблицями істинності булевої функції.

В таблиці кожній змінній та значенню функції відповідає по одному стовпчику, а кожній інтерпретації – один рядок.

х	j0	j1	j2	j3

Наведемо вигляд таблиці для n=1:

Тобто j₁(1) = 1; j₂(1) = 0; j₂(0) = 1;

Наведемо вигляд таблиці для n=2:

х

у

j0

j1

j2

j3

j4

j5

j6

j7

j8

j9

j10

j11

j12

j13

j14

j15

Тобто j₁(1, 0) = 0; j₁₂(1,0) = 0; j₆(0,1) = 1.

Кожній функції присвоюється порядковий номер у вигляді натурального числа, двійковий код якого зображує стовпчик значень відповідної функції. Наприклад, для функції j₁₂ для числа 12 = 1100₂ і для 1-ї інтерпретації j₁₂(0,0) = 1, j₁₂(0,1) = 1, j₁₂(1,0) = 0, j₁₂(1,1) = 0.

Більшість із розглянутих функцій часто використовують на практиці і мають певні позначення:

Функція	Позначка	Назва	Інші познач.	прочитання
j0(х, у)		Константа 0
j1(х, у)	хÙу=ху	Кон’юнкція (логічне і)	&,AND,min	х і у
j2(х, у)	ху	Заперечення імплікації	\	х і не у
j3(х, у)	х	Повторення першого аргументу		як х
j4(х, у)	ух	Заперечення оберненої імплікації	\	не х і у
j5(х, у)	у	Повторення другого аргументу		як у
j6(х, у)	хÅу	Виключає «або» (сума за модулем 2)	¹, XOR	х не як у
j7(х, у)	хÚу	Диз’юнкція (логічне «або»)	OR,+,max	х або у
j8(х, у)	х¯у	Заперечення диз’юнкції (стрілка Пірса)		не х і не у
j9(х, у)	х~у	Еквівалентність	Û, º	х як у
j10(х, у)		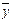Заперечення другого аргументу	Øy	не у
j11(х, у)	у®х	Обернена імплікація	Ì	х, якщо у
j12(х, у)		Заперечення першого аргументу	Øx	не х
j13(х, у)	х®у	Імплікація	Þ	якщо х, то у
j14(х, у)	x | y	Заперечення імплікації (штрих Шеффера)		не х або не у
j15(х, у)		Константа 1

Випишемо таблиці істинності для окремих логічних бінарних операцій.

х	у	хÚу

Диз’юнкція дає в результаті 1, якщо хоч один операнд дорівнює 1. Диз’юнкцію часто називають логічним додаванням, тому часто замість знака Ú використовують знак +.

Диз’юнкція 3-х і більше операндів також дає 1 в результаті, якщо хоч один з операндів має значення 1. Чотирьом інтерпретаціям відповідає код стовпчика результатів 0111, що є двійковим кодом числа 7, тобто в таблиці операція диз’юнкції приведена як j₇(х, у).

х	у	хÙу

Кон’юнкція дає в результаті 1, якщо всі операнди мають значення 1. Операцію також називають логічним множенням і замість позначки Ù використовують знак ·.

Кон’юнкція 3-х і більше операндів також дає 1 в результаті, якщо всі операнди мають значення 1. Чотирьом інтерпретаціям відповідає код стовпчика результатів 0001, що є двійковим кодом числа 1, тобто в таблиці операція кон’юнкції приведена як j₁(х, у).

х

Інверсія (заперечення) значення х має значення протилежне х. Це унарна операція в таблиці приведена як j₂(х). Аналогом позначки є позначка Øх.

х	у	х®у

Імплікація дає в результаті 0 тільки в одній інтерпретації (1, 0). Чотирьом інтерпретаціям відповідає код стовпчика результатів 1101, що є двійковим кодом числа 13, тобто в таблиці операція імплікація приведена як j₁₃(х, у).

х	у	х~у

Еквівалентність дає в результаті 1 тільки в інтерпретаціях (0, 0) і (1, 1). Чотирьом інтерпретаціям відповідає код стовпчика результатів 1001, що є двійковим кодом числа 9, тобто в таблиці операція імплікація приведена як j₉(х, у).

3 Булеві алгебри

Набір незалежних властивостей операцій Ú, Ù, Ø (замість них використаємо позначення +, ·, ̄) можна вважати аксіомами або незалежними законами булевої алгебри:

1. Комутативність: a + b = b + a, a · b = b · a;

2. Асоціативність: a + (b + с) = (a + b) + c, a · (b · c) = (a · b) · c;

3. Дистрибутивність: a + (b · с) = (a + b) · (a + с), a · (b + с) = (a · b) + (a · с);

4. Закони для нуля, одиниці і заперечення: a + 0 = a; a + 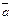=1; a · 0 = 0; a · 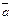=0;

Всі інші закони є наслідком перелічених 4-х. Зокрема:

5. Закон ідемпотентності: a + а = a · а = а;

6. Властивості одиниці і нуля: a + 1 = 1; a · 0 = 0;

7. Закони поглинання: a + (а · b) = a · (a + b) = a;

8. Закон інволюції (подвійного заперечення):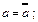

9. Закони де Моргана: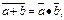

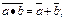
Булева алгебра – це алгебраїчна структура (В, +, ·, ̅, 0, 1) з бінарними операціями +, · В²®В, унарною операцією ̅ ® і виділеними операціями 0 і 1, які задовольняють властивостям 1-4.

Алгеброю логіки називають алгебраїчну структуру (В, +, ·, ̅, ®, ~), тобто це булева алгебра, доповнена операціями імплікації та еквівалентності.

Дата добавления: 2015-07-02