
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Передаточная функция цифрового КИХ-фильтра представляется в виде
|
|
|
|
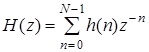 , ,
| (33) |
где импульсная характеристика имеет длительность N. Если импульсная характеристика цифрового КИХ-фильтра удовлетворяет следующему условию:
| h (n)= h (N –l– n), | (34) |
для n =0, 1,..., (N /2)–1, когда N четное, и для n =0, 1,..., (N –1)/2, когда N нечетное, то цифровой фильтр будет обладать линейной фазовой характеристикой.
В большинстве случаев именно потребность в линейной фазе или постоянном групповом времени вызывает необходимость применения цифровых КИХ-фильтров.
1. Метод частотной выборки.
Заданный уравнением (33) цифровой КИХ-фильтр имеет эквивалентное ДПФ-преобразование вида:
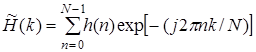 , ,
| (35) |
где 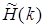 – в действительности дискретизированная N -точечная частотная характеристика цифрового фильтра с равномерно расположенными отсчетами. Вследствие этого импульсная характеристика h (n) и передаточная функция Н (z) цифрового КИХ-фильтра определяется через ДПФ (35) таким образом:
– в действительности дискретизированная N -точечная частотная характеристика цифрового фильтра с равномерно расположенными отсчетами. Вследствие этого импульсная характеристика h (n) и передаточная функция Н (z) цифрового КИХ-фильтра определяется через ДПФ (35) таким образом:
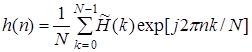
| (36) |
и 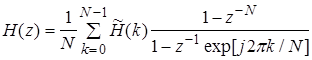 . .
| (37) |
Уравнение (37) является основным при расчете цифрового КИХ-фильтра.
Предположим, что частотная характеристика Hd (e jq) задана для частот– p < q < p. Это означает, что она определена и для всех частот q. Процедура расчета должна давать значения 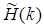 , т. е. дискретизированную N -точечную требуемую частотную характеристику с равномерным расположением отсчетов:
, т. е. дискретизированную N -точечную требуемую частотную характеристику с равномерным расположением отсчетов:
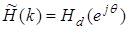 , при q =2 pk / N, , при q =2 pk / N,
| (38) |
где k =0, 1, 2, …, N –1. Используя непосредственно данные соотношения (38), можно получить подходящую КИХ-передаточную функцию из уравнения (37). Эта методика обеспечивает совпадение полученной и требуемой частотных характеристик в точках дискретизации q =2 pk / N для k =0, 1, 2,..., N –l.
2. Метод взвешивания.
Поскольку частотная характеристика Н (е jq) любого цифрового фильтра представляет собой периодическую функцию частоты q, она имеет разложение в ряд Фурье:
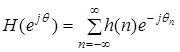 , ,
| (39) |
где 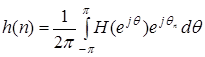 . .
| (40) |
Очевидно, что коэффициенты ряда Фурье h (n) фактически представляют собой импульсную характеристику цифрового фильтра.
Одним из возможных способов получения цифровых КИХ-фильтров, аппроксимирующих функцию Н (е jq), является усечение бесконечного ряда (39) до конечного числа членов. Однако из хорошо известного явления Гиббса следует, что усечение бесконечного ряда вызывает выбросы и колебания в требуемой частотной характеристике до и после любой точки разрыва. Кроме того, величина этих выбросов и колебаний не уменьшается с увеличением длины последовательности при условии сохранения ее конечности. Это по существу означает, что прямое усечение уравнения (39) для получения аппроксимации цифрового КИХ-фильтра не обеспечивает хороших результатов.
Метод взвешивания используется для получения конечных весовых последовательностей w (n), называемых окнами, которые модифицируют коэффициенты Фурье в уравнении (39) для получения требуемой импульсной характеристики hd (n) конечной длительности, где:
| hd (n)= h (n) w (n), | (41) |
а w (n) – последовательность конечной длительности, т. е. w (n)=0 для n > N и n <0. Из соотношения (41) следует, что результирующая импульсная характеристика hd (n) также имеет протяженность N отсчетов.
Поскольку умножение двух последовательностей во временной области эквивалентно свертке двух частотных характеристик в частотной области, метод взвешивания обеспечивает сглаживание выбросов первоначальной частотной характеристики, т. е. подавление ее отклонений и пульсаций. Недостатком является расширение переходной полосы.
Для завершения этого подраздела приведем некоторые характерные функции окна:
а) прямоугольное окно:
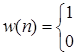
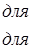
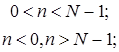
б) окно Бартлетта или треугольное окно:
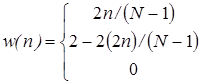
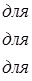
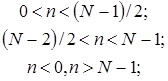
в) окно Ханна:
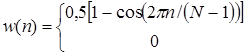
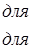
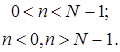
Как и в случае аналоговых фильтров, цифровые БИХ-фильтры не могут обеспечить совершенные линейные фазовые характеристики. В противоположность им цифровые КИХ-фильтры могут быть рассчитаны для обеспечения линейных фазовых характеристик. Кроме того, цифровые КИХ-фильтры всегда устойчивы. Это положительные качества цифровых КИХ-фильтров. К отрицательным чертам относится то, что исполнение цифрового КИХ-фильтра требует большего числа вычислений и большего числа цифровых элементов. Однако во многих ситуациях требуются цифровые КИХ-фильтры для выполнения тех задач, которые невозможно решить на основе цифровых БИХ-фильтров, а именно: получение фильтров с линейной фазой и многоскоростных фильтров, где входной и соответствующий выходной сигналы дискретизированы на разных скоростях.
2.3.3 Представление цифровых фильтров на z- плоскости.
Цифровой фильтр может быть синтезирован путем размещения полюсов и нулей передаточной функции на z- плоскости, основанном на следующих правилах:
1. Полюса и нули должны быть либо действительными, либо иметь комплексно-сопряженную пару.
2. Полюс в точке z=0 оказывает влияние на фазо-частотную характеристику фильтра и не изменяет амплитудно-частотную.
3. Полюс (или ноль) на единичной окружности означает, АЧХ на данной частоте бесконечно возрастает (или обращается в ноль).
4. Полюс вне единичной окружности означает, что фильтр нестабилен, т.е. отклик фильтра на импульс не затухает, а возрастает.
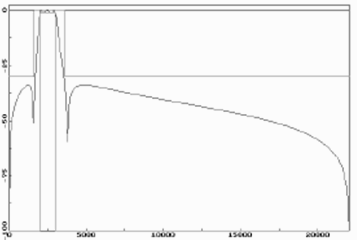
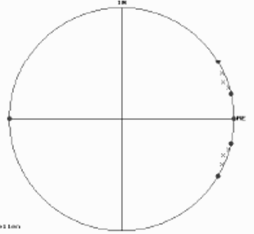
Амплитудно-частотная характеристика и представление на z- плоскости цифрового полосовой фильтр 6-го порядка, где:
• – ноль,  –полюс.
–полюс.
ИЗУЧЕНИЕ СВОЙСТВ И ПАРАМЕТРОВ ЦИФРОВЫХ ФИЛЬТРОВ
Целью работы является генерация сигнала, состоящего из нескольких гармоник, в системе MATLAB 6.1 и исследование в приложении Signal Processing Tool (SPTool) действия фильтров нижних, верхних частот, полосовых и режекторных фильтров на этот сигнал.
Первой задачей является генерация сигнала. Для этого запустите MATLAB 6.1. В начале создания некоторого сигнала зададим вектор-столбец времени t. Для этого в окне Command Window наберите строку:
>> t=(0:.01:2)’;
Эта команда задает изменение t от 0 до 2 с шагом 0,01 и обеспечивает дискретизацию сигнала по времени.
Теперь зададим вектор некоторой функции y(t), которая представляет собой сумму синусоиды с амплитудой 1 и частотой 1 Гц с синусоидой, имеющей амплитуду 0.25 и частоту 3 Гц:
>> y=sin(2*pi*1*t)+0.25*sin(2*pi*3*t);
Обратите внимание на то, что в этом выражении t – вектор, а потому и y тоже будет вектором. Частота f =1 Гц в первой компоненте сигнала указана в явном виде (как 1) только ради наглядности. Полезно учесть, что в большинстве расчетов MATLAB не использует размерные величины, поэтому лучше сразу привыкнуть к безразмерным величинам.
Теперь можно задать построение графика y(t):
>> plot(t,y);
Обрабатывать сигналы удобно используя приложение Signal Processing Tool (SPTool), которое вызывается следующей командой:
>> sptool
Чтобы импортировать сохраненный нами сигнал в это приложение выберите в меню File пункт Import… В раскрывшимся окне поставьте переключатель Source в положение From Workspace. В поле Workspace Contents выберите строку, в которой записано имя функции описывающей сигнал (в данном примере это y), и нажмите на верхнюю кнопку со стрелкой. В поле Sampling Frequency введите частоту дискретизации. Эта величина обратна шагу изменения времени t, заданному при формировании сигнала (в данном примере шаг изменения t равен 0,01, а частота дискретизации, следовательно, равна 100).
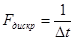
| (42) |
В поле Name записано имя, под которым будет значиться данный сигнал в приложении SPTool. На данной стадии это имя можно изменить по собственному усмотрению. Нажмите кнопку Ok.
Теперь в списке Signals наряду с именами встроенных сигналов появилось имя импортированного сигнала. Нажав кнопку View под списком Signals, можно посмотреть график выделенного сигнала.
В данном приложении можно проектировать и использовать цифровые фильтры для обработки сигналов. В списке Filters записаны имена трех встроенных фильтров. При нажатии кнопки View под списком Filters, появится окно Filter Viever. В нем можно посмотреть:
- АЧХ-фильтра (амплитуду можно задать либо в линейном, либо в логарифмическом масштабе либо в децибелах; частоту – либо в линейном, либо в логарифмическом масштабе);
- ФЧХ-фильтра (угол можно задать либо в радианах, либо в градусах; частоту – либо в линейном, либо в логарифмическом масштабе);
- групповое время задержки фильтра;
- нули и полюса фильтра;
- отклик на единичный импульс.
Нажав на кнопку New, получаем возможность проектирования фильтров. Кнопка Edit дает возможность редактировать ранее созданные фильтры. В раскрывшемся окне Filter Designer задаются параметры фильтра, производится расчет порядка фильтра и вывод АЧХ.
В поле Sampling Frequency введите частоту дискретизации обрабатываемого сигнала. В поле Algorithm можно выбрать один из следующих видов цифровых фильтров:
- КИХ-фильтр Ремеза;
- КИХ-фильтр с минимальным среднеквадратическим отклонением;
- КИХ-фильтр с окном Кайзера;
- БИХ-фильтр с аппроксимацией Баттерворта;
- БИХ-фильтр с аппроксимацией Чебышева;
- БИХ-фильтр с аппроксимацией инверсной Чебышева;
- БИХ-фильтр с эллиптической аппроксимацией.
Выбрав пункт Pole/Zero Editor можно задать с помощью мыши или вводя координаты на Z -плоскости полюса и нули передаточной функции.
Порядок фильтра либо рассчитывается (если стоит птичка в поле Minimum Order), если вводится в поле Order (если птичка снята). В данной работе порядок фильтров будет рассчитываться.
В поле Type задается тип фильтра: ФНЧ, ФВЧ, полосовой или режекторный фильтр.
Ниже вводятся граничные частоты и затухания полос пропускания и задерживания.
Все вносимые изменения будут тут же отображаться на графике, если поставить птичку в поле Auto Design.
Чтобы отфильтровать сигнал, выберите его в списке Signals, затем в списке Filters выберите фильтр и нажмите на кнопку Apply. В раскрывшимся окне введите (или оставьте введенное по умолчанию) имя отфильтрованного сигнала. Нажмите Ok. Теперь это имя добавилось в списке Signals. Посмотреть график отфильтрованного сигнала можно описанным выше способом.
Задание
1. Сгенерируйте сигнал, состоящий из трех гармоник с частотами 1, 3, и 5 Гц, имеющих амплитуды 1, 0.5 и 0.75 соответственно. Импортируйте этот сигнал в приложение SPTool и отфильтруйте его так, чтобы:
а) выделить первую гармонику;
б) выделить вторую гармонику;
в) выделить третью гармонику;
г) подавить только вторую гармонику;
используя для этого фильтры нижних, верхних частот, полосовой и режекторный (заградительный) фильтры.
2. Создайте БИХ-фильтр с аппроксимацией Баттерворта. Не меняя параметров фильтра, измените аппроксимацию с Баттерворта на Чебышева, затем на инверсную Чебышева и эллиптическую. Как при этом меняется АЧХ и порядок фильтра.
3. Создайте полосовые БИХ- и КИХ-фильтры с одинаковыми параметрами. Просмотрите АЧХ и ФЧХ данного фильтра. Сравните АЧХ, ФЧХ и порядки полученных фильтров.
4. Сформируйте два синусоидальных сигнала частотой 10 Гц и 20 Гц, длительностью 5 секунд и частотой дискретизации 1000 Гц.
Создайте полосовой БИХ-фильтр с аппроксимацией Чебышева со следующими параметрами:
- частота дискретизации – 1000 Гц;
- левая граничная частота полосы задерживания – 2 Гц;
- левая граничная частота полосы пропускания – 5 Гц;
- правая граничная частота полосы пропускания – 495 Гц;
- правая граничная частота полосы задерживания – 498 Гц;
- максимальное затухание в полосе пропускания – 1дБ;
- минимальное затухание в полосе задерживания – 60дБ.
Создайте полосовой КИХ-фильтр Чебышева (Equiripple FIR) с аналогичными параметрами.
Отфильтруйте сформированные сигналы с помощью созданных фильтров. Сравните сдвиг фазы между сигналами до фильтрации и после при использовании БИХ- и КИХ-фильтра.
5. С помощью редактора Pole/Zero Editor синтезируйте:
а) фильтр нижних частот;
б) фильтр верхних частот;
в) полосовой фильтр;
г) режекторный (заградительный) фильтр.
6. Запустите приложение Filter Design & Analysis Tool с помощью команды
>>fdatool
В данном приложении сформируйте полосовой КИХ-фильтр использую метод взвешенных функций (FIR Window) со следующими параметрами:
- порядок фильтра – 50;
- частота дискретизации – 2000 Гц;
- левая граничная частота – 250 Гц;
- правая граничная частота – 750 Гц.
Определите использование какой оконной функции дает наибольшее затухание передаточной функции на частоте 200 Гц. Какой минимальный порядок фильтра, передаточная функция которого имеет затухание 40 дБ на частоте 200 Гц?
Контрольные вопросы
1. Назовите 4 основных вида аналоговых фильтров-прототипов.
2. Какие фильтры являются рекурсивными (БИХ), а какие нерекурсивными (КИХ)?
3. Что такое групповое время задержки?
4. Назовите методы расчета БИХ-фильтров.
5. Достоинства и недостатки метода взвешивания при проектировании КИХ-фильтров.
6. Преимущества и недостатки БИХ- и КИХ-фильтров.
7. Как необходимо включать фильтры при создании эквалайзера.
|
|
|
|
|
Дата добавления: 2015-07-02; Просмотров: 3212; Нарушение авторских прав?; Мы поможем в написании вашей работы!