Декодирование принимаемой кодовой комбинации. 2 страница

Следующим этапом процедуры быстрого декодирования является определение локаторов ошибок 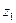и (блок 4 алгоритма рис. 1). Для этого, так же как и в лабораторной работе 2, сначала определим обратные им величины 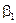и , являющиеся корнями полинома . В нашем случае в Matlab эту операцию можно выполнить с помощью команд:

.

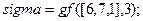
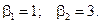В результате их выполнения получаем: , что соответствует Для нахождения значений локаторов ошибок 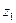и необходимо вычислить величины, обратные значениям найденных корней, т.е. . Это нетрудно сделать, воспользовавшись данными табл. П.2, или с помощью команды Matlab

.

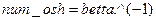В результате её выполнения выводятся значения , которые в степенном представлении (см. табл.П.2) соответствуют значениям 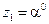и 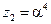. Это указывает на то, что ошибки в кодовой комбинации (10) находится на позициях, соответствующих и 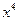в многочлене (12).

Для вычисления значений ошибок (блок 5 алгоритма рис. 1) воспользуемся алгоритмом Форни [4], по которому

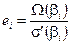, (19)

где − производная от полинома локаторов . Вычисление производной от многочлена над полем осуществляется по следующему правилу:

,

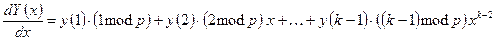причём выражение 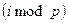для каждого 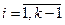вычисляется в обычной арифметике, а результат этого вычисления интерпретируется как элемент поля , и далее произведение этого элемента на соответствующий коэффициент 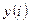, также являющийся элементом поля , определяется по правилам умножения поля [6].

Применяя данное правило к найденному полиному локаторов (17) над полем , находим, что . Подставляя этот результат в (19) и учитывая (18), с использованием арифметики поля 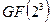получаем:

;

.

В Matlab эти вычисления можно выполнить с использованием команд:

;

;

.

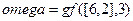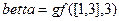После их выполнения получаем: .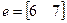

Найденные значения 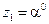; ; 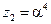и позволяют записать вычисленный полином ошибок в виде

,

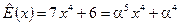после чего процедура исправления ошибок (блок 6 алгоритма рис. 1) сводится к сложению с (12), выполняемого по правилам поля 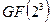. Это сложение даёт:

,

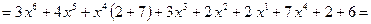
что соответствует вектору переданной кодовой комбинации 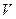(8).

4.4. Краткое описание алгоритма моделирующей программы и методики работы с ней.

Блок-схема укрупненного алгоритма моделирующей программы представлена на рис.1.1, она включает в себя 10 блоков. В блоке 1 осуществляется ввод определяющих режим моделирования данных. К их числу относятся: значение вероятности ошибки в дискретном канале, а также исправляющая способность исследуемого кода и число бит , содержащихся в одном символе кода РС.

В блоке 2 по заданным и определяются общее число недвоичных символов в блоке кода и число информационных символов , а также производится формирование последовательности передаваемых равнове роятных недвоичных сообщений (символов кода РС с объёмом алфавита 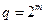), разбиение её на блоки, содержащие по символов, и кодирование их исследуемым кодом. В блоке 3 производится преобразование сформированной (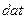) и закодированной (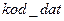) последовательностей 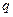-ичных знаков в двоичные (соответственно и ). Последовательности и необходимы для определения оценок вероятностей ошибок в канале и системе с кодеком, осуществляемого по двоичным символам; кроме того, сигнал подаётся далее на вход моделируемого двоичного канала. Посредством блоков 4, 5 и 6 осуществляется моделирование дискретного симметричного канала без памяти, включающего в себя передатчик (блок 4) и приёмник (блок 6) модема с фазоманипулированным (ФМ) сигналом и непрерывный канал (блок 5), имитирующий линию связи. В блоке 4 последовательность двоичных символов преобразуется в отсчёты соответствующего ей фазоманипулированного (ФМ) сигнала, передаваемого в канал связи. В качестве модели непрерывного канала в данной работе используется гауссов канал (т.е. канал с аддитивным гауссовским шумом). При этом соотношение «сигнал-шум» в непрерывном канале , где 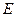− энергия одной посылки сигнала; 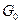− односторонний энергетический спектр шума, выбирается из условия обеспечения заданной вероятности ошибки в дискретном симметричном канале с ФМ, образуемом блоками 3, 4 и 5 рассматриваемой модели, на основе известного соотношения: 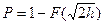, где 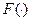− интеграл вероятностей. В блоке 5 осуществляется измерение энергии 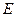модулированного сигнала, соответствующего передаче одного элементарного сообщения, а затем формируются отсчеты дискретного белого гауссовского шума, энергетический спектр которого при измеренном значении 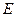обеспечивает заданное на моделирование отношение «сигнал-шум» 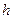. Отсчеты этого шума складываются с отсчетами передаваемого сигнала, формируя тем самым выходной сигнал непрерывного канала.

В блоке 6 производится моделирование оптимального приемника ФМ сигнала, осуществляющего его демодуляцию.

В блоке 7 полученные в результате демодуляции оценки принимаемых символов сравниваются с символами последовательности , сформированными на выходе блока 3; при несовпадении фиксируются ошибки. Отношение количества обнаруженных ошибок к общему числу переданных символов кода и представляет собой оценку вероятности ошибки в дискретном канале.

В блоке 8 полученные после демодуляции двоичные кодовые символы преобразуются в последовательность 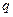-ичных знаков, что необходимо для выполнения операции декодирования, осуществляемой в блоке 9. Результат декодирования в этом же блоке преобразуется в двоичные символы, которые в блоке 10 сравниваются с с символами последовательности , сформированными на выходе блока 3. При несовпадении символов фиксируются ошибки. Отношение числа ошибок к общему количеству знаков последовательности (которое меньше числа переданных символов, содержащихся в , поскольку отражает только информационные символы передаваемых кодовых комбинаций кода РС) и представляет собой оценку вероятности ошибки в системе с кодеком.

Для запуска моделирующей программы необходимо в командном окне системы Matlab набрать название программы lab_rab_3 и нажать клавишу Enter. Также программу можно запустить щелчком левой кнопки мыши по кнопке Run (зелёный треугольник) на панели инструментов окна Editor системы Matlab (при условии, что в этом окне активирована программа lab_rab_3). После запуска программы в командном окне появляется сообщение: “Введите значение вероятности ошибки в канале без кодека p=”. При его получении нужно ввести (т.е. набрать в командном окне) значение в соответствии с вариантом задания и нажать клавишу Enter. При этом в качестве символа, разделяющего целую и дробную части числа при его десятичном представлении следует использовать не запятую, а точку. Получив два последующих сообщения “Введите значение исправляющей спосбности t =” и “Введите число бит, содержащихся в одном символе кода m =”нужно аналогичным образом ввести запрашиваемые программой данные. После этого начинается выполнение программы. Этапы её выполнения индицируются сообщениями, выводимыми на экран (в командном окне). По окончании выполнения программы в командном окне выводятся значения (p_kan) и (p_kod), являющиеся результатами компьютерного эксперимента.

Контрольные вопросы

1. Как связаны параметры кодов Рида-Соломона ( и ) с количество двоичных элементов , содержащихся в одном символе кода РС, и исправляющей способностью кода (выраженной в количестве недвоичных символов) ?

2. Изложите методику определения порождающего многочлена кода Рида-Соломона.

3. Изложите методику кодирования с использованием кода Рида-Соломона.

4. Изложите методику определения синдрома.

5. Изложите сущность алгоритма быстрого декодирования кодов Рида-Соломона.

6. Какую задачу решает алгоритм Берлекэмпа-Месси? В чём заключается его преимущество по сравнению с алгоритмом Питерсона-Горенстейна-Цирлера?

7. Расскажите, как реализуются вычисления, предписываемые алгоритмом Берлекэмпа-Месси (по рис.2).

8. Как определяются коэффициенты многочлена локаторов ошибок?

9. Какую задачу решает алгоритм Форни?

10. Расскажите, как реализуются вычисления, позволяющие одновременно с реализацией алгоритма Берлекэмпа-Месси определить многочлен значений ошибок (по рис.2).

11. В чём заключается сущность алгоритма Форни?

12. Как осуществляется вычисление производной от многочлена над полем ?

13. Как определяется число ошибок в принятой кодовой комбинации при реализации алгоритма быстрого декодирования кодов Рида-Соломона.?

14. Как определяется местонахождение ошибок в принятой кодовой комбинации и как они исправляются?

15. Как построена моделирующая программа (привести ее алгоритм)?

16. Как оценивается вероятность ошибки в дискретном канале (без кодека) и в системе с кодеком?

17. Как зависит вероятность ошибки в системе с кодеком от исправляющей способности и скорости кода?

Литература

1.Конспект лекций.

2. Султанов Б.В., Иванов А.П., Геращенко С.М. Математические основы построения помехоустойчивых блочных кодов. Учебное пособие. ПГУ, 2006.

3. Султанов Б.В., Дорошкевич В.В. Методические указания к лабораторной работе № 2 «Коды БЧХ». ПГУ, 2012.

4. Блейхут Р. Теория и практика кодов, контролирующих ошибки.− М. «Мир», 1986.

5. Кларк Дж. мл., Кейн Дж. Кодирование с исправлением ошибок в системах цифровой связи. – М.: Радио и связь, 1987.

6. Ван дер Варден. Алгебра..− М. «Наука», 1979.

Приложение

Таблица П.1.1. Варианты заданий к п. 3 − 4 лабораторной работы 3.

№ вар.	(задание)

Таблица П.1.2 Варианты заданий к п.5 лабораторной работы 3

№ вар.
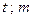
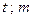
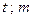
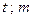
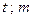
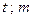
	0.01	1;3	2;3	1;4	2;4	3;4	3;5
	0.015	2;4	3;4	4;4	3;5	4;5	5;5
	0.025	3;4	4;4	5;4	3;5	4;5	7;5
	0.05	4;4	5;4	6;4	5;5	6;5	13;5
	0.007	1;3	2;3	1;4	2;4	3;4	3;5
	0.012	2;4	3;4	4;4	3;5	4;5	5;5
	0.048	4;4	5;4	6;4	5;5	6;5	12;5
	0.033	3;4	4;4	5;4	4;5	5;5	10;5
	0.021	2;4	3;4	4;4	3;5	4;5	7;5
	0.058	4;4	5;4	6;4	5;5	6;5	13;5
	0.027	3;4	4;4	5;4	3;5	4;5	10;5
	0.039	4;4	5;4	6;4	5;5	6;5	12;5
	0.013	2;4	3;4	4;4	3;5	4;5	7;5
	0.035	3;4	4;4	5;4	4;5	5;5	11;5
	0.009	1;3	2;3	1;4	2;4	3;4	4;4
	0.049	4;4	5;4	6;4	6;5	8;5	12;5
	0.019	2;4	3;4	4;4	3;5	4;5	8;5
	0.0335	3;4	4;4	5;4	4;5	5;5	11;5
	0.011	1;3	2;3	1;4	2;4	3;4	4;4
	0.03	3;4	4;4	5;4	4;5	5;5	10;5
	0.042	4;4	5;4	6;4	5;5	6;5	12;5
	0.029	3;4	4;4	5;4	4;5	5;5	10;5
	0.0455	4;4	5;4	6;4	5;5	6;5	12;5
	0.014	1;3	2;3	1;4	2;4	3;4	4;4
	0.02	2;4	3;4	4;4	3;5	4;5	8;5
	0.034	3;4	4;4	5;4	4;5	5;5	11;5
	0.022	2;4	3;4	4;4	3;5	4;5	8;5
	0.04	4;4	5;4	6;4	5;5	6;5	12;5
	0.017	2;4	3;4	4;4	3;5	4;5	7;5
	0.044	4;4	5;4	6;4	5;5	6;5	12;5
	0.023	2;4	3;4	4;4	3;5	4;5	8;5
	0.032	3;4	4;4	5;4	4;5	5;5	11;5
	0.043	4;4	5;4	6;4	5;5	6;5	12;5
	0.038	3;4	4;4	5;4	4;5	5;5	11;5
	0.056	4;4	5;4	6;4	5;5	6;5	13;5
	0.024	2;4	3;4	4;4	3;5	4;5	8;5
	0.047	4;4	5;4	6;4	6;5	8;5	12;5
	0.0255	2;4	3;4	4;4	4;5	5;5	9;5
	0.031	3;4	4;4	5;4	4;5	5;5	10;5
	0.055	4;4	5;4	6;4	5;5	6;5	13;5
	0.026	2;4	3;4	4;4	4;5	5;5	9;5
	0.016	2;4	3;4	4;4	3;5	4;5	6;5
	0.0355	3;4	4;4	5;4	4;5	5;5	11;5
	0.046	4;4	5;4	6;4	6;5	8;5	12;5
	0.028	3;4	4;4	5;4	4;5	5;5	10;5
	0.037	3;4	4;4	5;4	4;5	5;5	11;5
	0.041	4;4	5;4	6;4	6;5	8;5	12;5
	0.018	2;4	3;4	4;4	3;5	4;5	7;5
	0.036	3;4	4;4	5;4	4;5	5;5	11;5
	0.045	4;4	5;4	6;4	6;5	8;5	12;5

Таблица П.2. Представления элементов поля (расширения поля по модулю примитивного многочлена )

Степенное	Многочленное	Двоичное	Десятичное

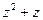
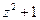
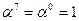
Дата добавления: 2015-07-02