Устройство и принцип действия гравиметра астазированного кварцевого (ГАК)

ГАК состоит из 2 частей: сосуда Дьюара, горизонтального маятника Голицына, обычно, в такого вида гравиметрах термостаты отсутствуют, они снабжены только мощной теплозащитой, роль которого играет сосуд Дьюара.

Рассмотрим принцип работы горизонтального маятника Голицына (рисунок 5.2).

Рисунок 5.2 – Схема действия горизонтального маятника Голицына

На конце стержня ОС установлен груз. Пружина АВ держит стержень ОС в состоянии равновесия. Пружина соединена со стержнем ОВ с помощью плеча. Если изменится сила тяжести, то стержень будет стремиться изменить свое положение, растягивая пружину. В какой-то момент времени система придет в состояние равновесия, т. к. пружина будет стараться компенсировать изменение силы тяжести своими упругими свойствами, т. е. упругие моменты силы тяжести и пружины будут равны. Плечо упругой силы в системе маятника Голицына d₂ мало по сравнению с плечом силы тяжести d₁, поэтому для того, чтобы уравновесить изменение силы тяжести, необходимо большое изменение упругой силы Q. Уравнение равновесия запишется следующим образом

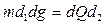, где 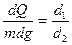. (5.3)

т. е. приращение упругой силы Q должно быть настолько больше прирашения силы тяжести, насколько плечо d₁ больше плеча d₂. Говоря по-другому, в такой системе небольшие изменения силы тяжести вызовут большие растяжения пружины и соответственно большие углы поворота маятника. Это есть астазирование системы. При измерениях используется метод компенсации, при котором горизонтальная составлющая не оказывает влияния.

5.4 Способы измерений вторых производных силы тяжести. В некоторых случаях измеряется не сила тяжести, а ее производные. Эти величины измеряются всегда статическим способом. Путем интегрирования вторых производных силы тяжести и можно всегда перейти к значениям самой силы тяжести. Измерение основано на принципе сравнения положений равновесия крутильной упругой системы, устанавливающейся под действием гравитационного поля массы системы, расположенные в двух близких точках. На упругой нити подвешивается коромысло с массами на концах. Оно устанавливается в некотором положении равновесия, которое определяется степенью неоднородности гравитационного поля и упругостью крутильной нити. В разных точках с разной степенью неоднородности поля равновесие наступит под разными углами закручивания нити, по величине которой судят о вторых производных потенциала силы тяжести. Приборы, основанные на этом принципе, называются вариометрами или градиентометрами.

Основная литература 1 осн [94-203], 2 осн [99-195]

Дополнительная литература 1 доп [169-279]

Контрольные вопросы:

1. Какими методами пользуются в настоящее время для определения силы тяжести?

2. Классификация гравиметров.

3. Устройство и принцип работы гравиметра астазированного кварцевого.

4. С помощью чего добиваются астазирования в ГАКе?

5. Какими приборами можно измерять вторые производные потенциала силы тяжести?

Дата добавления: 2015-07-02