Влияние конечной толщины лопаток на напор насоса

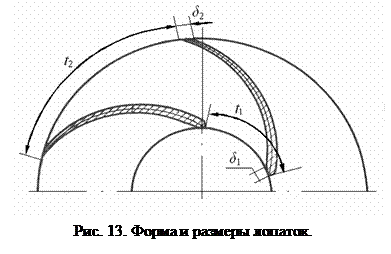При выводе основного уравнения Эйлера для лопаточного насоса было сделано допущение о том, что лопатки рабочего колеса насоса имеют бесконечно малую толщину. Но практически это не так. Обычно толщина лопаток в средней части (при различных размерах рабочего колеса) составляет 2…8 мм. Входная часть лопаток утолщена и закруглена по кромке, а выходная часть имеет минимальную толщину и может заканчиваться острой кромкой. В сечении лопатка напоминает профиль крыла самолета (рис. 13). При входе жидкости в межлопаточный канал она испытывает сжатие, её скорость увеличивается, линии тока искривляются, а при выходе – сечение увеличивается и скорость жидкости снижается.

Выявим влияние основных размеров проточной части межлопаточного канала на скорость движения жидкости при её входе в межлопаточный канал.

При бесконечно малой толщине лопаток теоретический расход жидкости через сечение межлопаточных каналов на входе колеса будет равен:

Q _т= 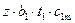, (18)

где z – число лопаток; b ₁ – ширина лопаточного канала; t ₁ – шаг лопаток; с _1m – меридиональная скорость.

При конечной толщине лопаток этот же расход вычислим по формуле:

Q _т= 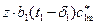, (19)

где δ ₁ – толщина лопатки; - меридиональная скорость жидкости при конечной толщине лопаток.

Приравнивая правые части уравнений (18) и (19) и выполняя простые преобразования, определим меридиональную скорость жидкости на входе в межлопаточное пространство при конечной толщине лопаток:

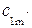= s ₁, где s ₁= - коэффициент, учитывающий уменьшение сечения межлопаточного канала на входе, s ₁=1,10 …1,25.

План скоростей для рассмотренного случая приведен на рис. 14. Компоненты скорости и углы, относящиеся к случаю конечной толщины лопаток содержат индекс «к»; меридиональная скорость для конечной толщины лопаток отмечена верхним индексом «*».

Как следует из плана скоростей, компоненты скорости движения жидкости, входящие в уравнение Эйлера (с _1u и u ₁), остались неизменными и это может привести к выводу о том, что конечная толщина лопаток не оказывает влияния на напор насоса. Однако на самом деле преобразование скорости движения жидкости по величине и направлению (при её входе в межлопаточный канал) сопровождается потерями энергии.

Рассмотрим движение жидкости в выходном сечении межлопаточного канала, т.е. при выходе жидкости их межлопаточного канала. План скоростей для этого случая приведен рис. 15. Из приведенного плана скоростей видно, что при конечной толщине лопаток план скоростей меняется аналогично входному сечению: увеличивается меридиональная скорость на величину Δ с _2m, изменяются по величине и направлению абсолютная и относительная скорости движения жидкости, однако окружная составляющая абсолютной скорости c _2u остается неизменной. Используя методику, аналогичную той, которая была применена при рассмотрении движения жидкости на входе в рабочее колесо, представляется возможным установить зависимость между меридиональной скоростью 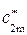при конечной толщине лопаток и той же скоростью с _2m при бесконечно малой толщине лопаток. Эта зависимость запишется в виде:

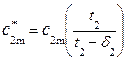= s ₂, где s ₂= 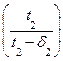- коэффициент, учитывающий уменьшение сечения межлопаточного канала на выходе, s ₂=1,05 …1,15.

Таким образом, в результате теоретического исследования по выявлению влияния толщины лопаток на характер движения жидкости в межлопаточном пространстве установлено, что лопатки конечной толщины приводят к увеличению скорости движения жидкости в межлопаточном пространстве и к её изменению по величине и направлению при входе в межлопаточный канал и выходе из него. На преобразование скорости жидкости по величине и направлению на входе жидкости в межлопаточный канал и выходе из него затрачивается некоторая часть энергии, которая относится к гидравлическим потерям. Эти потери аналогичны известным в гидравлике потерям на сжатие и расширение. В литературе такие потери часто называют кромочными потерями. Кромочные потери при оптимальной форме лопаток не велики и их объединяют с другими гидравлическими потерями. Для снижения потерь энергии входные кромки лопаток выполняют закруглёнными, а выходные – минимальной толщины и даже – острыми.

2.8. Угол β ₂ и его влияние на напор насоса.

Теоретические исследования и результаты экспериментальных исследований показывают, что напор насоса и его к.п.д. существенно зависят от угла β ₂.

Проведем теоретические исследования следующим образом. Предположим, что мы имеем три насоса с одинаковыми значениями подачи Q _т, размерами рабочих колес (r ₁, r ₂, b ₁, b ₂, z), а следовательно и с одинаковыми значениями c _2m и u ₂.

Будем считать, что α ₁=90⁰, т.е. вход жидкости на лопатки радиальный и, кроме того, c _1m= c _2m= c ₁ – const.

Далее примем, что угол β ₂ первого насоса меньше 90⁰, второго - β ₂=90⁰ и третьего β ₂ больше 90⁰.

Изобразим план скоростей на выходе из рабочего колеса и определим из него окружную составляющую абсолютной скорости c _2u:

c _2u= u ₂ - c _2mctg β ₂. (20)

Подставив значение c _2u в уравнение Эйлера (9а) получим:

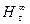= . (21)

Анализируя уравнение (21) видно, что при некоторой величине угла β ₂ теоретическое значение напора будет равно нулю. Очевидно, это возможно, если 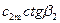= . Угол β ₂ в этом случае будет иметь минимальное значение:

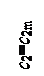
ctgβ _2min= 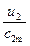. (22) Из выражения (22) видно, что скорости u ₂ и c _2m в этом случае должны представлять собой катеты прямоугольного треугольника, у которого c ₂= c _2m (рис. 16).

Пусть угол β ₂=90⁰ (рис.17), тогда ctg β ₂=0 и согласно уравнению (21) напор насоса будет равен:

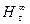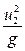= . (23)

В этом случае напор насоса имеет максимальную величину и зависит только от числа оборотов n, т.к. по принятому условию значение размеров колеса принято постоянным. Относительная скорость в этом случае w ₂= c _2m= c _1m= c ₁., а окружная скорость u ₂= c _2u.

Величина динамического напора, согласно выражению (13) будет равна:

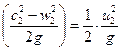= = . (24)

Сопоставляя выражение (24) с (23) видно, что динамический напор при угле β ₂=90⁰ составляет половину от полного напора насоса. Следовательно, полный напор, создаваемый насосом, состоит на половину из статического и на половину из динамического:

= .

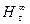Рассмотрим случай с третьим насосом, у которого угол β ₂>90⁰. Для удобства рассуждений примем, что c _2u=2 u ₂ (рис. 18). Тогда полный напор насоса будет равен: 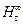= . (25)

Сопоставляя выражение (25) с (23) видим, что полный напор насоса в этом случае представлен только в динамической форме. При больших значениях угла β ₂ насос работать не сможет, т.к. в этом случае динамический напор будет больше, чем полный напор.

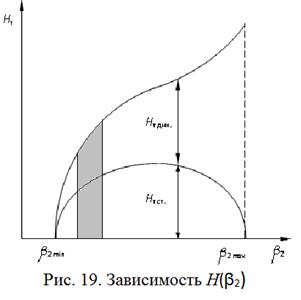
Зависимость напора насоса от угла β ₂ приведена на рис. 19. У современных насосов угол лопаток на выходе колеса принимают в пределах от 15⁰ до 30⁰; в редких случаях он может иметь значение 50⁰ (на рис. 19 обозначено серым цветом).

Дата добавления: 2015-07-02