Порядок выполнения исследований

1. В соответствии с вариантом задания (таблица 2.2.1) и со схемой фильтра (рисунок 2.2.2) выбрать элементы наборного поля для использования их в качестве парных симметричных элементов фильтра.

Таблица 2.2.1 – Варианты задания

Вариант	Частота среза fс, кГц	Тип фильтра	Схема фильтра	Номинальное значение парных элементов наборного поля	E, В
	1,5	ФНЧ	Т	L/2=70 мГн	12
	1,0	ФВЧ	Т	2С=0,25 мкФ	14
	1,8	ФНЧ	Т	L/2=30 мГн	16
	1,5	ФВЧ	Т	2С=0,1 мкФ	10
	1,6	ФНЧ	Т	L/2=50 мГн	12
	1,0	ФВЧ	Т	2С=0,5 мкФ	16
	2,0	ФВЧ	П	2L=30 мГн	16
	1,1	ФНЧ	П	С/2=0,5 мкФ	10
	1,5	ФВЧ	П	2L=50 мГн	12
	2,3	ФНЧ	П	С/2=0,1 мкФ	14
	1,8	ФВЧ	П	2L=20 мГн	14
	1,5	ФНЧ	П	С/2=0,25 мкФ	10

Подобрать два ближайших по значению элемента для симметрии в паре. Для этого необходимо соединить последовательно все имеющиеся в лаборатории элементы указанного в задании номинала, подать синусоидальное напряжение (например, частотой 1 кГц) и, измеряя вольтметром падение напряжения на каждом из элементов, выявить два таких элемента, на которых падения напряжения будут наиболее близки друг к другу.

Уточнить параметр одного из выбранных элементов пары экспериментальным путём: используя вольт- и амперметр, определить его реактивное сопротивление при подаче синусоидального сигнала частотой 1кГц, а затем через сопротивление рассчитать его индуктивность (ёмкость).

Рассчитать и записать параметр пары без коэффициентов ½ и 2.

Рассчитать значение одиночного элемента фильтра (см. рисунок 2.2.2) через формулу для частоты среза f_с (её значение указано в задании), исходя из найденного параметра пары без коэффициентов ½ и 2.

Подобрать третий элемент наборного поля с номиналом, ближайшим меньшим к рассчитанному через частоту среза f_с.

Уточнить параметр одиночного элемента фильтра через его сопротивление при подаче синусоидального сигнала частотой 1кГц.

Исходя из уточнённых (фактических) параметров (L и C) элементов фильтра пересчитать значение частоты среза f_с и рассчитать период среза Т_с [ мс ] и использовать в дальнейшем эти значения f_с и Т_с.

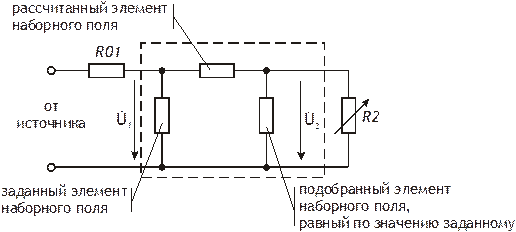
2. Собрать фильтр в соответствии со схемой, указанной в варианте задания, и с рисунками 2.2.2 и 2.2.3. При этом для ограничения тока, потребляемого от источника переменного напряжения, последовательно с фильтром на его входе включить резистор R01 (элемент наборного поля №01).

В качестве нагрузки фильтра R2 выбрать блок переменного сопротивления. Рассчитать характеристическое сопротивление фильтра ρ по фактическим значениям L и C и установить R2=ρ.

3. Подключить блок переменного напряжения и задать значение ЭДС (см. таблицу 2.2.1) синусоидальной формы при частоте, равной значению f_с, полученному из фактических значений L и C в конце п.1. Частоту выставить, ориентируясь по соответствующему значению периода Т_с с помощью осциллографа.

а)

б)

Рисунок 2.2.3 – Схема исследуемого фильтра: а) Т-образная; б) П-образная.

4. Экспериментально определить с помощью осциллографа период Т_с и частоту среза f_с по достижении равенства U₂ =0.707 U₁, регулируя частоту источника. При этом необходимо одновременно контролировать значения U₂ и U₁, имея в виду, что при изменении частоты меняется не только U₂, но и U₁, а важно добиться их соотношения U₂ / U₁ =0.707.

В случае расхождения экспериментально найденного значения f_с с расчётным более чем на 10% выяснить причину и повторить измерения. В дальнейшем за основу взять экспериментально найденные значения f_с и Т_с.

5. Для последующих измерений рассчитать по формуле 2.2.1 и занести в таблицу 2.2.2 значения частот и периодов сигнала источника (исходя из последних значений f_с и Т_с) для диапазона относительных частот ν = 0.5÷2 с шагом 0.1, причём в интервале ν = 0.9÷1.1 (в зоне частот близких к границе полос) снизить шаг до 0.05.

Выставляя частоту источника по рассчитанным значениям и контролируя её через период при помощи осциллографа, измерить напряжения U₁ и U₂ и занести их значения в таблицу 2.2.2.

Таблица 2.2.2 – Данные эксперимента и коэффициенты передачи и затухания

№ п/п	ν	f, кГц	T, мс	U1, В	U2, В	η	А, Нп	А, дБ
	0,5
...	...

6. По измеренным значениям напряжений U₁ и U₂ рассчитать для каждой частоты значения коэффициента передачи η=U₂ / U₁ и коэффициентов затухания А по формулам 2.2.8 и 2.2.10. Построить график частотной характеристики η(ν).

7. Построить расчётную АЧХ коэффициента затухания А [ дБ ] (ν) для фильтра с идеализированными элементами при работе на согласованную нагрузку в диапазоне частот ν = 0.5÷2 (см. формулу (2.2.13) для полосы затухания).

На эту расчётную характеристику нанести в виде отдельных точек экспериментальные значения коэффициента затухания А [ дБ ] из таблицы 2.2.2.

8. Построить расчётную ФЧХ В°(ν) идеального фильтра в режиме согласованной нагрузки в диапазоне частот ν = 0.5÷2, рассчитав фазовый сдвиг в градусах. (см. формулу (2.2.12) для полосы пропускания).

9. Для исследования прохождения через фильтр сигналов несинусоидальной формы подать от источника переменного напряжения сигнал, по выбору, прямоугольной или треугольной формы при частоте ν = 0.5. Формы сигналов u₁(t) и u₂(t) зарисовать с экрана осциллографа.

10. Объяснить, как исследуемый фильтр изменил гармонический состав несинусоидального сигнала (подавление или пропускание основной и высших гармоник в составе сигнала).

11. Сделать вывод по работе, в котором привести описания всех частотных зависимостей коэффициентов фильтра с целью доказательства его избирательных свойств. Описания графиков проводить, сравнивая значения параметров в диапазонах низких и высоких частот и обосновывая то, что один из диапазонов является полосой пропускания, а другой — полосой затухания.

Также указать, как повлияло сопротивление нагрузки на характеристику коэффициента затухания фильтра.

Рекомендуемая литература по теме:

1. Курулёв А. П. и др. Теория электрических цепей… – Мн., 1999: глава 10 и §9.5

2. Основы теории цепей Г. В. Зевеке и др. – М., 1989: глава 18 и §8.5

3. Бессонов Л. А. Теоретические основы электротехники. М., 1996: глава 5 и §4.10

Дата добавления: 2015-07-02