Краткая теория. Соленоид представляет собой провод, навитый в виде спирали на цилиндрический каркас (рис.1)

Соленоид представляет собой провод, навитый в виде спирали на цилиндрический каркас (рис.1). В теории электромагнитных явлений большую роль играет воображаемый бесконечно длинный соленоид. Особенностью такого соленоида является то, что его магнитное поле ограничено объемом соленоида и однородно. Можно провести аналогию с бесконечным плоским конденсатором, обладающим такими же свойствами по отношению к электрическому полю.

Силовые линии однородного магнитного поля бесконечно длинного соленоида параллельны его оси, и их направление связано с направлением тока в витках правилом правого винта.

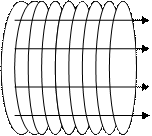В Рис.1

I

Величина магнитной индукции бесконечно длинного соленоида прямо пропорциональна силе тока в нем (I) и числу витков, приходящихся на единицу длины (n): B=μ₀nI,

Где μ₀ – магнитная постоянная.

Данное выражение можно получить, используя теорему о циркуляции (закон полного тока).

Циркуляция вектора магнитной индукции равна интегралу:

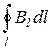, где B_l – проекция вектора магнитной индукции на направление обхода контура.

Теорема о циркуляции: Циркуляция вектора магнитной индукции по произвольному замкнутому контуру равна алгебраической сумме токов, охватываемых этим контуром, умноженной на магнитную постоянную:

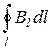= μ₀∑I_i.

Рассмотрим бесконечно длинный соленоид (на рисунке 2 изображена часть соленоида), по которому течет ток I. Выберем замкнутый контур АВCD прямоугольной формы так, чтобы сторона АВ лежала внутри соленоида и была параллельна его оси.

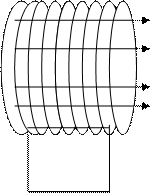Рис.2

Тогда циркуляция вектора В может быть представлена как сумма 4-х интегралов:

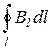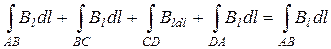= = BL, (1)

Где L – длина стороны АВ.

Интегралы по остальным трем участкам выбранного контура обращаются в ноль, так как на этих участках равна нулю либо сама индукция магнитного поля, либо ее проекция на данный участок контура.

Сумма токов, охватываемых данным контуром, равна произведению тока в одном витке на число витков, укладывающихся на отрезке АВ длиной L:

∑I_i = IN=InL (2)

(используем n=N/L).

Подставляя (1) и (2) в выражение теоремы о циркуляции, получим:

BL = μ₀InL, отсюда

В = μ₀In.. (3)

Реальные катушки не являются бесконечно длинными, но если длина соленоида намного больше его диаметра, то на участках, достаточно удаленных от концов соленоида, поле можно считать однородным и использовать для определения индукции формулу (3). Если же длина соленоида ненамного превосходит диаметр, то его поле не будет однородным. Величина и направление магнитной индукции в разных точках будут различны, и чем ближе к концам соленоида – тем неоднородность поля будет проявляться сильнее.

Дата добавления: 2015-07-02