Гармонические колебания в контуре

Закон Ома для неоднородного участка цепи: 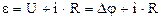, где - сопротивление элементов контура.

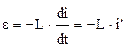
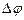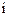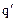В колебательном контуре: = - разность потенциалов на обкладках конденсатора. Подставив в исходное уравнение, получим: . Поскольку сила тока = , а 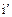= , то уравнение примет вид: .

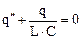Это - дифференциальное уравнение второго порядка. При оно перепишется: . Решением такого уравнения является функция , где - фазовый угол (или фаза колебаний), который выражается в радианах, - начальная фаза колебаний (при t=0), - собственная круговая частота колебаний в контуре. Сила тока в колебательном контуре: .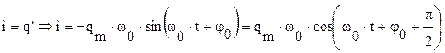

Напряжение в контуре: .

В математике и физике колебания, которые подчиняются синусоидальному закону, называются гармоническими.

Максимальное значение функции называют амплитудой.

В гармонических колебаниях значение функции становится максимальным, если cos или sin становятся равными 1. Таким образом, амплитуда колебаний силы тока в контуре , а амплитуда колебаний напряжения на конденсаторе .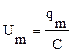

Закон колебаний силы тока в соленоиде и напряжения на конденсаторе можно получить при начальной фазе :

; .

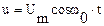Отсюда следует, что в колебательном контуре фаза колебаний силы тока в катушке отстает от фазы колебания напряжения на конденсаторе на угол 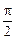(рисунок 39).

		Рисунок 39. Гармонические колебания, сдвинутые на

Время, затраченное на одно полное колебание, называется периодом колебаний Т (рисунок 39).

Число колебаний в единицу времени называется частотой колебаний 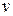. . 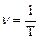Размерность частоты:

[ ]=1 Гц (герц).

Рисунок 40. Гармонические колебания силы тока  

Один герц – это частота, при которой одно полное колебание происходит за одну секунду.

В выражении 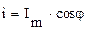угол 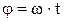, где угловая частота . Тогда ток в любой момент времени :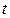

Период собственных колебаний контура 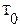определяется формулой Томпсона: .

Отсюда: 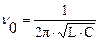– собственная частота колебаний в контуре и . Из этих формул следует, что при достаточно малых значениях L и C в контуре можно получить электромагнитные колебания высокой частоты, измеряемые миллионами герц и больше.

В реальном электрическом контуре из-за потерь энергии на нагревание проводников и диэлектриков энергия магнитного и электрического полей постепенно превращается во внутреннюю энергию и колебания через некоторое время прекращаются. Такие колебания называются затухающими.

При период колебаний

Дата добавления: 2015-07-02