Пример 7. См. [В. С. Владимиров], дополнение, §2, задачи 5, 6

,.

,,,.

.

Подставляя это выражение вместо u в данную задачу, получим:

.

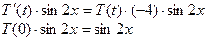Замечаем теперь, что 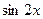всюду является общим множителем, сократив на который, мы получим уже обыкновенную (!) задачу Коши для нахождения неизвестной пока функции T (t):

. Отсюда, конечно, .

Таким образом,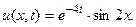

Замечание. Нас выручило то обстоятельство, что правая часть 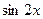начального условия нашей задачи Коши оказалась собственной функцией оператора (относящейся к числу -4). В самом деле, (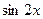) = (-4) . (☺)

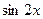Напомним, что вообще, собственной функцией какого-либо линейного оператора T называется функция f = f (x) 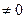, для которой существует такое число 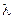, называемое собственным числом, что .

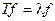Если бы не соотношение (☺), нам бы не удалось сократить на 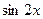и, тем самым, исключить из задачи переменную x, что, в свою очередь, и привело нас к простой обыкновенной задаче для функции .

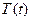Технически, именно на использовании этого удобного свойства собственных функций и основан метод Фурье. Возникает, однако, два вопроса:

1) Собственные функции какого именно дифференциального оператора должны нас интересовать?

2) Каковы эти собственные функции?

Ответ на первый вопрос гласит: нам интересны собственные функции оператора дифференцирования по той переменной, от которой зависит краевое условие решаемой задачи. Так, начальное условие 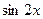из примера 1 зависит от x. Поэтому, естественно спрашивать, является ли 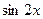собственной функцией именно оператора , а не, скажем, , также входящего в наше уравнение.

Ответ на второй вопрос таков. Можно (и даже желательно) заранее найти все собственные функции интересующего нас оператора T из уравнения .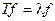

Упражнение 1. Найдите все собственные функции оператора . (Подсказка: все собственные числа этого оператора вещественны).

Упражнение 2. Найдите все собственные функции оператора , имеющие период 2π.

Упражнение 3. Решите задачу Коши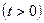

Обратите внимание на важную особенность задач Коши из примера 1 и упражнения 3. Обе они включали лишь по одной известной функции 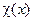не равной нулю, которые, к тому же, были собственными функциями соответствующего дифференциального оператора (в этих случаях ­‑ оператора ). При этом под известными функциями понимаются правые части краевых условий, а также свободный член дифференциального уравнения. Так, в примере 1 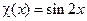, а в упражнении 3 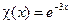. Подобные задачи будем называть простейшими.

Пример 1+. Решите задачу Коши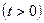

Решение. Данная задача является простейшей. Действительно, в эту задачу входит только одна ненулевая известная функция – правая часть ye ^{-3 x} в первом начальном условии. При этом ye ^{-3 x} является собственной функцией оператора 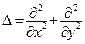, относящейся к числу 9 (проверьте!). Стало быть, решение данной задачи следует искать в виде 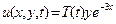. Подставив эту функцию в уравнение и начальные условия нашей задачи, получим:

.

Видим, что на сомножитель ye ^{-3 x} везде можно сократить. Останется обыкновенная задача Коши для неизвестной пока функции T (t):

.

Общее решение уравнения этой задачи T (t) = C ₁ e ^{3 t} + C ₂ e ^{-3 t}. Применив начальные условия, получим C ₁ = C ₂ = 0,5. Так что T (t) = ch3 t, а .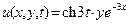

Итак, простейшая задача Коши – это задача, содержащая единственную ненулевую известную функцию , где 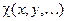- собственная функция оператора 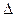(в правых частях начальных условий считаем ).

В нижеследующих примерах 2, 3 предложенные задачи Коши не являются простейшими. Однако, они могут быть разложены на простейшие с помощью так называемого принципа суперпозиции. Принцип суперпозиции заключается в использовании линейности дифференциальных уравнений и краевых условий задач математической физики, а также линейности операторов дифференцирования, входящих в эти уравнения.

Поясним сказанное на примерах.

Пример 2. Решить задачу Коши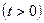

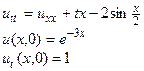
Заменим данную задачу следующими вспомогательными простейшими задачами:

Легко заметить, что эти задачи получены из исходной путем замены на нули всех известных функций, входящих в исходную задачу, кроме одной, своей для каждой из вспомогательных задач.

Если мы решим эти четыре вспомогательные задачи, то есть найдем функции u ¹, u ², u ³, u ⁴, то решением исходной задачи будет их сумма u = u ¹+ u ²+ u ³+ u ⁴. В самом деле, 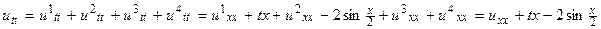, то есть уравнение исходной задачи удовлетворяется. Далее, , , 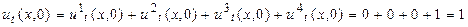то есть выполнены и начальные условия.

Найдем, для примера, слагаемое u ¹. Обратим внимание, что x – собственная функция для оператора , ибо (x) = 0 = 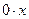. Поэтому u ¹ можно искать в виде u ¹ = T (t) x.

Подставляя это выражение вместо u ¹, получим: 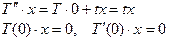. Сократив везде на x (эффект собственной функции!), получим обыкновенную задачу Коши для T (t) 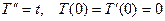. Отсюда легко найти, что 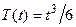, а значит u ¹(x, t) = . Остальные слагаемые находятся аналогично.

Упражнение 4. (Не обязат.) Найдите остальные слагаемые в примере 2.

До сих пор нам встречались примеры, в которых в правых частях уравнений и в краевых условиях фигурировали собственные функции (оператора ): 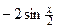, x, 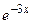и т. п. В этих примерах нам удавалось отыскать неизвестную функцию в виде произведения такой собственной функции на неизвестную пока функцию T (t).

Как же находить решение краевой задачи, когда правая часть уравнения, либо краевого условия не является собственной функцией?

Пример.3 Решить задачу Коши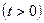

Решение. Здесь не является собственной функцией для (проверьте!). Заметим, однако, что 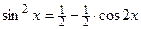. Обе функции – константа 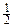и 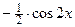- уже собственные для . Стало быть, нам нужно решить задачу

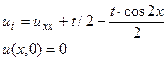, решение которой, согласно принципу суперпозиции, можно искать в виде u = u ¹ + u ², где

Упражнение 5. (Необязат.) Найдите функции u ¹ и u ² из примера 3.

В примере 3 мы выразили "неудобную" функцию через две собственные (то есть "удобные" для нас). В принципе, их количество могло бы быть любым, в том числе и бесконечным. И если в примере 3 для выражения "неудобной" функции через "удобные" мы просто воспользовались тригонометрической формулой, то в общем случае "неудобную" функцию, скажем f (x), приходится разлагать в ряд Фурье по системе "удобных", скажем, e ₁(x), e ₂(x),..., e _n(x),...:

. Здесь 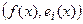- скалярное произведение, понимаемое обычно в смысле некоторого гильбертова пространства L ₂(a; b), то есть

= .

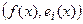В таком случае, естественно, и искомая функция u ищется в виде u = 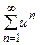с тем, чтобы слагаемые 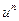найти уже из простейших задач.

Вышеизложенные приёмы используются и для решения краевых задач других типов (а не только задач Коши). При этом, как и ранее, если исходная задача не является простейшей, нужно её разложить на простейшие. Повторимся, что "удобными" для нас служат всегда собственные функции соответствующего дифференциального оператора (вроде ), отвечающие ещё, быть может, некоторым нулевым граничным условиям на концах промежутка (a; b).

Далее нам понадобятся формулы для оператора Лапласа в полярных, цилиндрических и сферических координатах.

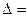
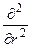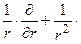
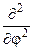+ (полярные координаты).

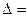
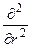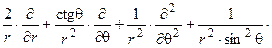
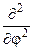+ (сферические координаты).

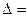
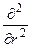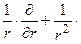
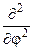+ + (цилиндрические координаты).

Упражнение 6. Решите стационарную задачу в круге r < 2:

Указание. Перейдите к полярным координатам. Используйте собственные функции, найденные в упражнении 2.

Упражнение 7. Решите стационарную задачу в круге r < 2:

.

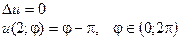Указание. Разложите граничное условие в ряд Фурье по системе, найденной в упражнении 2. Затем воспользуйтесь принципом суперпозиции.

Упражнение 8. Решите стационарную задачу в кольце 1 < r < 2:

.

Пример 4. (Задачник Владимирова В.С., §16, №21.5). Найти функцию, гармоническую внутри сферы (то есть в шаре) радиуса R и такую, что

(u + u_r)(R, φ, θ) = sinθ(sinφ+ cosφcosθ + sinθ). (1)

Решение. По определению, функция u – гармоническая, если она удовлетворяет уравнению Лапласа Δ u = 0. Сообразуясь с формой данной области, перепишем уравнение Лапласа в сферических координатах:

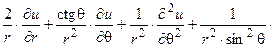
+ = 0 (2)

Правая часть граничного условия (1) зависит от φ,θ. Поэтому нам нужно выразить её линейно через собственные функции дифференциального оператора по переменным φ,θ. Как мы видим, в уравнении (2) это оператор

Θ = 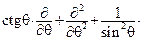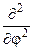(3)

(Предварительно мы умножили уравнение (2) на r ²).

Собственные функции оператора (3) называются сферическими функциями. Их явные выражения можно найти в [Владимиров В. С.], §16, стр. 200, формула (23), а также стр. 201, перед задачей 16.20. Важно отметить, что постоянным коэффициентам a _k, b _k, c _k, и т.д. можно придавать произвольные значения. Любая полученная таким образом по формулам стр. 201 (или (23) на стр. 200) функция Y_n (φ,θ),будет собственной для оператора (3), относящейся к числу λ _n = - n ( n +1). То есть

Θ(Y_n) = 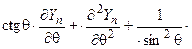= 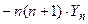(4)

В данном (и подобных) примере естественно попробовать найти желаемое выражение, используя тригонометрические преобразования и не прибегая к процедуре разложения в ряд Фурье.

sinθ(sinφ+ cosφcosθ + sinθ)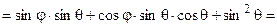

.

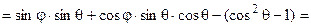
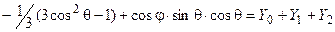Таким образом, согласно принципу суперпозиции, исходную задачу надо разделить на три вспомогательные простейшие задачи:

, ,

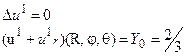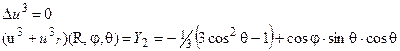(5).

Найдем, для примера, функции u ¹ и u ³. u ¹ ищем в виде произведения u ¹= 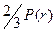. Подставляем это выражение в первую вспомогательную задачу, имея в виду, что уравнение Лапласа выражено в сферических координатах (см. (2)). Поскольку 2/3 = Y ₀, то, согласно (4), Θ(Y ₀) = Θ(2/3) = 0, а значит, мы получаем

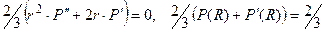, или, сокращая на 2/3 (‑ собственная функция!):

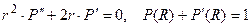. Далее, решаем дифференциальное уравнение.

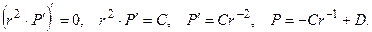По смыслу задачи, искомая функция должна иметь смысл в центре шара, то есть при r = 0. Это невозможно, если С ≠ ≠ 0, ибо тогда сомножитель P (r) теряет смысл. Значит, С = 0 и P (r) = D = const. Теперь из граничного условия находим, что D = 1. Отсюда P (r) = 1 и u ¹ = 2/3.

Замечание. Если решение задачи ищется не внутри, а вне сферы, то из соображений ограниченности решения, наоборот, полагают D = 0.

u ³ также ищем в виде Y ₂(φ,θ)∙ P (r) . Это выражение подставляем в задачу (5). Снова принимая во внимание, что Θ(Y ₂) =

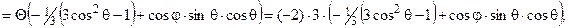согласно (4), получаем из (5):

Сокращая везде на собственную функцию 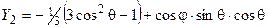, получаем:

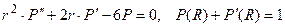. Получилась обыкновенная задача с уравнением Эйлера. Его коэффициенты не постоянны! Можно искать частные решения в виде r^a. Подстановка в уравнение вместо P дает

Таким образом, 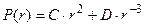- общее решение уравнения. Рассуждая аналогично предыдущему случаю, заключаем, что D = 0. Из граничного условия находим C: .

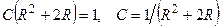Итак,

Упражнение 9. Найдите функцию u ² из предыдущего примера.

Пусть область, в которой поставлена краевая задача, имеет вид ограниченного цилиндра высоты h и радиуса R. Тогда, разумеется, уместен переход к цилиндрическим координатам (так, чтобы ось О z совпадала с осью цилиндра). При этом граничные условия на основаниях цилиндра (при z = 0 и z = h) будут зависеть от r (возможно, и от φ, но мы такие случаи рассматривать не будем). Следовательно, возникает потребность в нахождении собственных функций (и собственных чисел) оператора 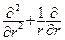. Уравнение для таких функций P = P (r) записывается в виде 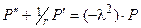(6), то есть, собственное число обозначено через (-λ²).

Уравнение (6) переносом всех членов в левую часть, умножением на r ² и введением новой переменной x = λ r сводится к уравнению Бесселя (порядка 0)

.

Общее решение этого уравнения выражается через функции Бесселя нулевого порядка первого рода J ₀(x) и второго рода Y ₀(x):

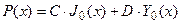, или .

Известно, что J ₀(x) определена, а Y ₀(x) не определена при x = 0. По тем же соображениям, что и в примере 4, полагают C = 0, если задача вне цилиндра или D = 0, если внутри. Оставшуюся константу находят из граничного условия на боковой поверхности r = R цилиндра.

Пример 5. В круговом цилиндре радиуса R и высоты h найти решение 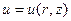задачи

.

Решение. В цилиндрических координатах уравнение данной задачи запишется так: 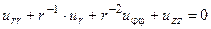, или, с учетом независимости искомой функции от полярного угла, .

Согласно принципу суперпозиции мы должны разделить нашу задачу на две:

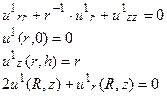
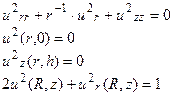
Решим сначала первую из них.

Граничное условие r предстоит линейно выражать через собственные функции оператора 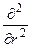+ 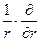. Причем эти собственные функции P = P (r) должны ещё отвечать граничному условию данной задачи при r = R. То есть, должно выполняться равенство . Перед примером 5 объяснялось, что . Теперь 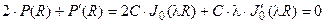, 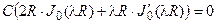. (7) Приравнять С к нулю нельзя. Необходимо, чтобы . Это будет выполнено, если λ R = μ – корень уравнения . (*) Известно, что уравнение (*) имеет последовательность (положительных) корней 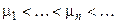. Следовательно, при 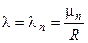равенство (7) будет выполнено (при любом С). Итак, можем положить 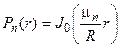. (8)

Замечание. Обратите внимание, что уравнение (*), а значит и его корни μ_n, определяются по граничному условию при r = R той задачи, которую Вы решаете. Хотя при дальнейшей записи решения эта индивидуальность и не видна.

Система (8) образует базис в так называемом "весовом" гильбертовом пространстве всех функций f, для которых конечен интеграл 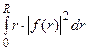, со скалярным произведением .

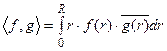Разложим граничное условие r решаемой нами задачи (для функции u ¹) в ряд Фурье по базису (8):

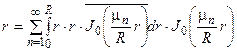(9)

Коэффициенты этого разложения, для краткости, обозначим через а_n.

Соответственно (9), функцию u ¹ тоже будем искать в виде 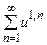(10)

Слагаемые же u ^{1, n} найдем из задач

(11 _n)

Понятно, что здесь мы поступили согласно принципу суперпозиции. Мы добились того, что все получившиеся задачи в качестве единственного ненулевого граничного условия содержат собственную функцию оператора 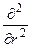+ 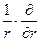, удовлетворяющую, к тому же, соответствующему граничному условию при r = R. Это позволяет находить решения этих задач в виде u ^{1, n} = ∙ Z_n (z). (12) Заметим, что тогда граничное условие на боковой поверхности r = R выполнено автоматически. Далее, как и во всех подобных случаях ранее, надо (12) подставить в (11 _n), учитывая, что 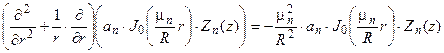. Будет:

Как и полагается, собственная функция всюду сокращается и остается:

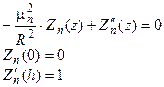
Общее решение последнего дифференциального уравнения удобно выразить через гиперболические функции:

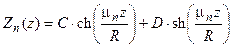. Первое из граничных условий дает С = 0, второе – D = 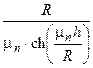. Таким образом, . Подставив полученное выражение в (12), найдем u ^{1, n}. Подставив же, в свою очередь, u ^{1, n} в (10), получим u ¹.

Упражнение 10. Найти функцию u ² из примера 5.

Указание: Граничное условие 1 = 1(z) выразить посредством ряда Фурье по системе собственных функций оператора , отвечающих граничным условиям при z = 0 и z = h.

Упражнение 11. Найти функцию u, гармоническую внутри цилиндра радиуса 3 и высоты 10, если

.

Упражнение 12. Найти функцию u, гармоническую внутри цилиндра радиуса 3 и высоты 10, если

.

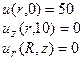Указание. Подумайте сначала, в чем существенная разница между двумя последними задачами, и можно ли ею воспользоваться для упрощения решения.

Выше мы изучали технику применения метода Фурье для задач Коши или, напротив, для стационарных задач в областях стандартного вида. Это значит, что дифференциальные уравнения были снабжены или только начальными, или только граничными условиями. Теперь мы рассмотрим задачи с условиями обоих видов, то есть так называемые смешанные задачи.

В сущности, к смешанным задачам метод Фурье применяется точно так же, как и к прочим, с одним лишь добавочным предварительным этапом работы. А именно, в первую очередь надо от исходной смешанной задачи перейти к задаче с нулевыми граничными условиями. Решение же последней ищется так же, как и ранее.

Пример 6. Решить смешанную задачу о распределении температуры внутри неограниченного кругового цилиндра радиуса R, если поверхность цилиндра имеет постоянную температуру u ₀, а начальная температура равна cos r.

Решение. Обозначим через 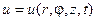искомую температуру. Здесь r, φ, z – цилиндрические координаты точки цилиндра, t – время. Принимая во внимание симметрию цилиндра относительно угла φ и его однородность по высоте z, а также независимость краевых условий от этих переменных (температура поверхности постоянна, а начальная температура зависит только от r), можем считать, что 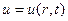. Тогда математическая формулировка задачи будет следующей:

Сначала перейдем от данной задачи к задаче с нулевым граничным условием. Для этого подберем какую-нибудь (возможно более простую) функцию, удовлетворяющую только данному граничному условию. Понятно, что нам подходит 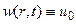. Теперь решение нашей задачи будем искать в виде 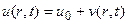. Подставим это выражение в нашу задачу. Получим смешанную задачу для новой искомой функции v:

Как видим, здесь уже нулевое граничное условие. Полученную задачу решаем теперь в точном соответствии с общей схемой метода Фурье. В частности, это означает, что полученную задачу надо первым делом разложить на простейшие задачи. Ненулевая (известная) функция есть только в правой части начального условия. Она зависит от r. Значит, она должна быть линейно выражена через собственные функции оператора 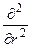+ 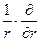, отвечающие нулевому граничному условию при r = R. Ранее мы находили, что этими функциями являются 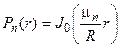, где, в нашем случае, μ_n – корни уравнения 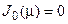. Выразим теперь наше граничное условие 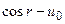в виде ряда Фурье по системе 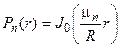, : 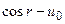= 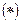. (Здесь множитель перед интегралом является результатом нормировки собственных функций; весь коэффициент ряда, для краткости, обозначен через а _n.)

В соответствии с разложением 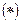, решение v (r, t) ищем в ви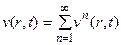де

, где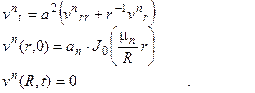

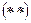
Решение (простейших) задач 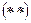уже можно искать в виде 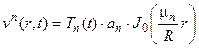. Подставим это выражение вместо v ⁿ в 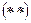. Получим:

При этом последнее условие выполнено автоматически, ибо 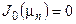. Сократив везде на собственную функцию , получим несложную обыкновенную задачу для T_n (t): откуда T_n (t) = 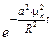. Осталось подставить найденное в формулу для v ⁿ, затем v ⁿ – в ряд для v и мы получим:

.

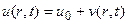
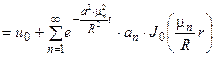Дата добавления: 2015-07-02