Дисперсия и поглощение

По решению задач по теме

Методические указания

Е.Я. Файн, м.б. Файн, В.П.Филиппенко

Пример оформления компьютерной презентации дипломной работы

Слайд 1	Слайд 2
Слайд 3	Слайд 4
Слайд 5	Слайд 6
Слайд 7	Слайд 8
Слайд 9	Слайд 10
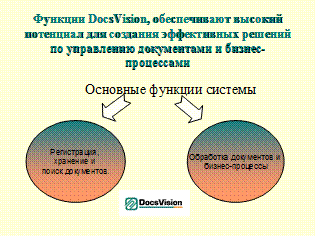Слайд 11	Слайд 12
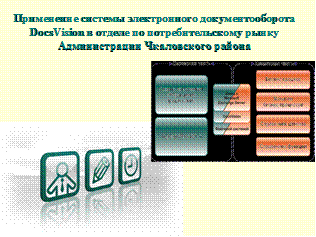Слайд 13	Слайд 14
Слайд 15	Слайд 16
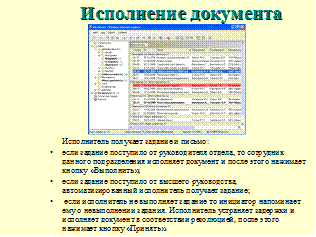Слайд 17	Слайд 18
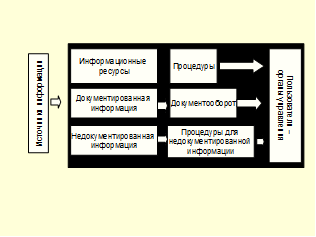Слайд 19	Слайд 20

«Дисперсия света. поглощение света»

Ростов-на-Дону

Краткая теория:

Дисперсия света – это явления, обусловленные зависимостью показателя преломления вещества от длины волны (или частоты):

n=f(l),

где l - длина волны света в вакууме.

Дисперсия вещества - производная dn/ dl.

Нормальной дисперсии соответствует интервал длин волн, в котором

dn / dl<0.

Аномальной дисперсии соответствует интервал длин волн, в котором

dn / dl>0.

Вакуум дисперсией не обладает.

Основное уравнение дисперсии:

n² = 1+ .

e = ,

где b = n₀q²/ e₀m = N₀e² /e₀m_e.

N₀ - концентрация электронов.

Групповая скорость:

.

Закон Бугера: ,

где- I₀ – интенсивность света на входе в поглощающий слой,

l- толщина слоя,

c - постоянная, зависящая от свойств поглощающего вещества – коэффициент поглощения.

Закон Рэлея:

~ w ⁴ ~ 1/l,

где -интенсивность рассеянного света,

w - частота.

Задача 1 /Ир5. 216/

Электромагнитная волна с частотой ω распространяется в разрежённой плазме. Концентрация свободных электронов в плазме равна N₀. Пренебрегая взаимодействием волны с ионами плазмы, найти зависимость:

а) электрической проницаемости плазмы от частоты

б) фазовой скорости от длины волны λ в плазме.

1) , где - квадрат плазменной частоты, е и m соответственно заряд и масса электрона, - электрическая постоянная.

Таким образом

Этот результат очевидным образом следует из основного уравнения дисперсии

в котором в случае плазмы(свободных электронов) собственные частоты колебаний ω_0к=0

2) Как следует из волнового уравнения для электромагнитного поля и определения абсолютного показателя преломления

Так как , а , причём ,

где λ₀ – длина волны в вакууме, и в плазме ,

то имеем и

Откуда .

Тогда .

Под корнем все величины положительны, корень больше 1 и υ>с.

Ответ:

.

Задача 2./Ир 5.222/

Исходя из определения групповой скорости U, получить формулу Рэлея U=V-l dV/dl. показать также, что U вблизи l= l¢ равна отрезку V¢, отсекаемому касательной к кривой V(l) в точке l¢.

Решение:

V 1. По определению групповая скорость .

Как известно, фазовая скорость может быть

представлена в виде V= w / k, откуда w= V k.

y^¢ Подставляя это выражение для w в

определение групповой скорости и произведя

дифференцирование, получаем:

l¢ l

Очевидно, .

По определению модуля волнового вектора k=2p/l.

Тогда и ,

что дает групповой скорости - формула Рэлея.

2. Рассмотрим график зависимости V =V(l) и касательную к нему в точке l¢.

Касательная составляет с осью l угол a, причем

V tga= . Очевидно V(l¢) =V¢ +l¢ tga /

V(l¢) l¢ tga Откуда .

y^¢ Сопоставление с формулой Рэлея U=V-l dV/dl

дает вблизи l= l¢, U=V¢.

l¢ l

Задача 3./Ир 5.223/

Найти зависимость между групповой U и фазовой V скоростями для следующих законов дисперсии:

а) V~1/

б) V ~ k

в) V ~ 1/w,

здесь l, k, w - длина волны, волновое число и круговая частота.

Дано: Решение:

а) V ~ 1 Ищем зависимости в соответствии с формулой

б) V ~ k Рэлея U=V-l dV/dl

в) V ~ 1/w а) V= ,

U=f(V)-? =V+la .

C учетом закона дисперсии V= имеем U=V+V/2=3/2V.

б) V ~ k. Выразим закон дисперсии через l с учетом k= : V=b/a,

тогда .

в) V ~ а/w². выразим закон дисперсии через l с учетом определения фазовой скорости V= w / k.

w= V k= 2pV/l.

Тогда V= , откуда V³= и V= bl^2/3, где b – новая константа.

Согласно формуле Рэлея

U=V - .

Ответ: а) 3/2V

б) 2V

в) .

Задача 4. /Ир 5.232/

Пучок света интенсивности I₀ падает нормально на плоскопараллельную пластинку толщины l. Пучок содержит все длины волн от l₁ до l₂ одинаковой спектральной интенсивности. Определить интенсивность прошедшего через пластинку пучка, если в этом диапазоне длин волн показатель поглощения зависит от l в пределах от c₁ до c₂ и коэффициент отражения каждой поверхности равен r. Вторичным отражением пренебречь.

Дано: Решение:

I₀ Пренебрегая рассеянием и зависимостью коэффициента

L отражения от длины волны, можем воспользоваться

l₁ законом Бугера: .

l₂ Закон изменения показателя поглощения c по условию

c₁ имеет вид ,

c₂ откуда .

r Спектральная интенсивность(точнее спектральная

I_пр-? плотность интенсивности) i_l =dI/dl, одинакова для всех длин волн, поэтому она равна i_l =I₀/(l₂-l₁). Тогда интенсивность пучка в диапазоне dl равна dI_l0= ,а закон Бугера для этого пучка можно записать в виде dI_l= или с учетом линейной зависимости c от l

.

Коэффициент отражения на передней и задней поверхностях плоскопараллельной пластинки одинаков и по условию задачи для всех длин волн одинаков, не зависит от длины волны. Тогда интенсивность прошедшего в интервале длин волн пучка можно записать в виде

,

так как вторичными отражениями по условию задачи можно пренебречь.

Проинтегрируем по длине волны в пределах от l₁ до l₂:

= .

В результате получим:

Ответ: .

Задача 5. /Ир5.233/

Светофильтр представляет собой пластинку толщиной d с показателем поглощения зависящим от длины волны l по формуле c(l) = a(1-l/l₀)², где a и l₀ - некоторые постоянные. Найти ширину полосы пропускания светофильтра Dl - ширину, при которой ослабление света на краях полосы в h раз больше, чем ослабление при l₀. Коэффициент отражения rот поверхностей светофильтра считать одинаковыми для всех длин волн.

Дано: Решение:

d Как показано в предыдущей задаче, исходя из

l закона Бугера, можно получить для интенсивности

c(l) = a(1-l/l₀)² пучка в интервале длин волн, прошедшего через Dl-? светофильтр:

h

r

Так как i_l dl - интенсивность падающего пучка в этом же интервале длин волн, то ослабление составляет:

.

Ослабление при l = l₀ составляет, как видно .

По условию ослабление на краях полосы пропускания в h раз больше, чем при l₀:

= h =

l - l₀ составляет половину ширины полосы пропускания светофильтра Dl/2.

Тогда ,

откуда

и окончательно получаем

.

Ответ:

Дата добавления: 2015-07-02